4.3.Тема: середні величини у статистиці

При підготовці до даної теми необхідно звернути увагу на наявність декількох засобів розрахунку середніх величин.

Середньою величиною в статистиці називається характеристика однотипних явищ, що свідчить про типовий рівень ознаки в розрахунку на одиницю сукупності.

Види середніх величин:

1. Середня арифметична найчастіше часто застосовується в розрахунках. Вона буває простою і зваженою.

Застосовується в тих випадках, коли відомий обсяг сукупності (m) і частота ознаки (f), або значення ознаки (х) і частота ознаки (f).

Середня арифметична проста розраховується по формулі:

де - середнє значення ознаки;

x_i - варіанта (конкретне значення ознаки);

n - число варіант.

Застосовується, коли кожна варіанта (ознака) зустрічається один раз або однакову кількість разів.

Наприклад:

Заробітна плата трьох робітників: 150 грн; 170 грн; 200 грн.

Визначити середню заробітну плату робітників.

Середня арифметична зважена розраховується за формулами:

де - середнє значення ознаки;

х - варіанта;

f - частота ознаки;

m - обсяг сукупності (m = x  f );

- відносна частота (питома вага частоти ознаки в загальному обсязі).

ТИПОВА ЗАДАЧА

Розрахувати середню заробітну плату робітників виходячи з таких умов:

Таблиця 8

Цех	Ситуація 1		Ситуація 2		Ситуація 3
	Заробітна плата грн./люд	Кіль-кість робітників, люд.	Фонд оплати праці , грн.	Кіль-кість робітників, люд .	Заро-бітна плата, грн/ люд	Питома вага робітни-ків у загаль-ній кількос-ті , %
	(x)	(f)	(m)	(f)	(x)	()
1	200	320	4000	20	200	10.0
2	160	150	24000	150	160	75.0
3	130	30	39000	30	130	15.0
Ра-зом	-	200	31900	200	-	100

Середня заробітна плата робітників:

Ситуація 1:

Ситуація 2:

Ситуація 3:

2. Середня гармонійна - це величина обернена до середньої арифметичної, з обернених значень ознаки.

Застосовується в тих випадках, коли відсутні частоти, а є дані про варіанти (х) і обсяги сукупності (m).

Середня гармонійна проста застосовується при однакових обсягах сукупності і розраховується по формулі:

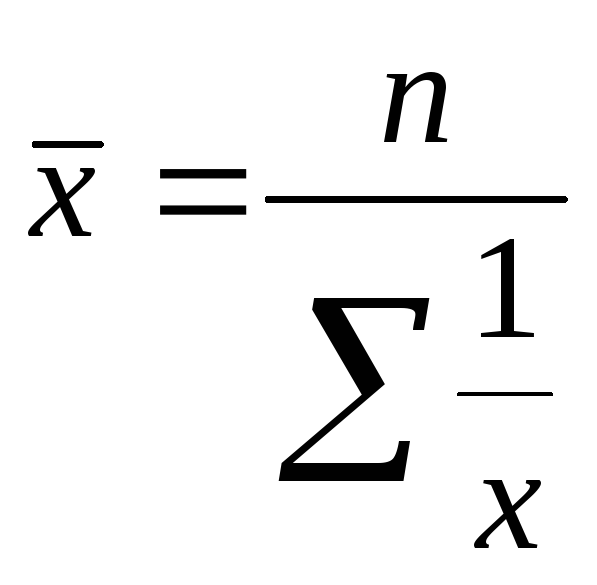
де n - число варіант

х - варіанта;

- середнє значення ознаки.

Середня гармонійна зважена застосовується при різноманітних обсягах сукупності і розраховується по формулі:

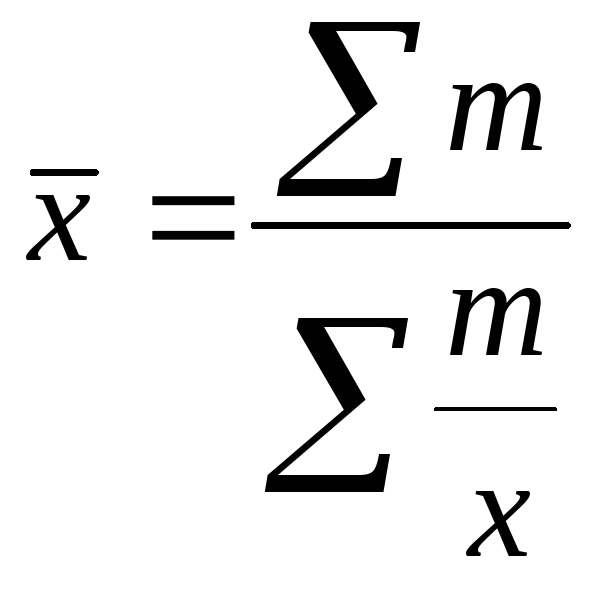
де m - обсяг сукупності;

х - варіанта;

- середнє значення ознаки.

ТИПОВА ЗАДАЧА

Розрахувати середню заробітну плату робітників виходячи з таких умов:

Таблиця 9

Цех	Ситуація 1		Ситуація 2
	Заробітна плата робітників, грн./люд. (х)	Фонд оплати праці, грн. (m)	Заробітна плата робітників, грн./люд. (х)	Фонд оплати праці, грн. (m)
1 2 3	200 150 130	4000 24000 3900	200 100 150	6000 6000 6000
Всього	-	31900	-	18000

Середня заробітна плата робітників:

Ситуація 1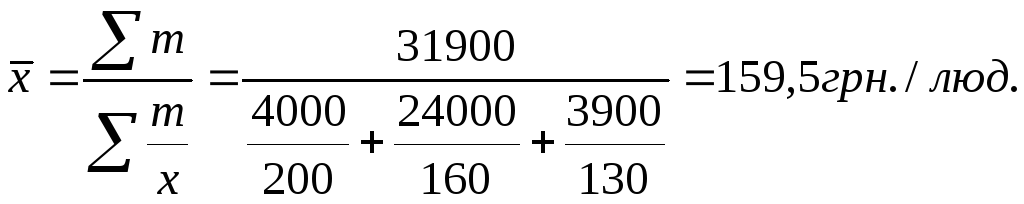

( - кількість робітників цеху №1 і т.д.)

Ситуація 2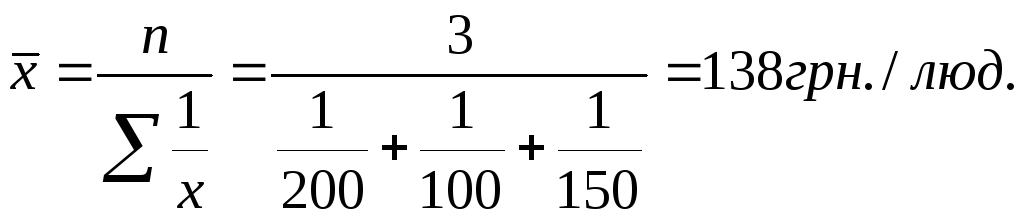

У ситуації 2 розрахунок середньої заробітної плати можна виконати за допомогою середньої арифметичної зваженої:

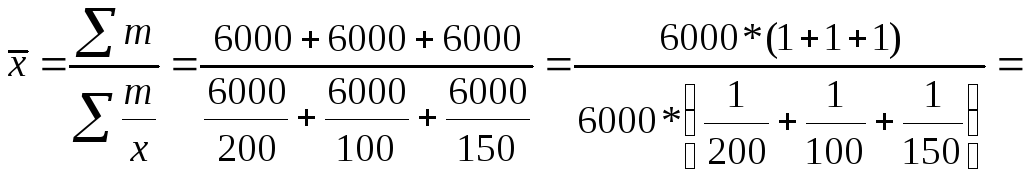
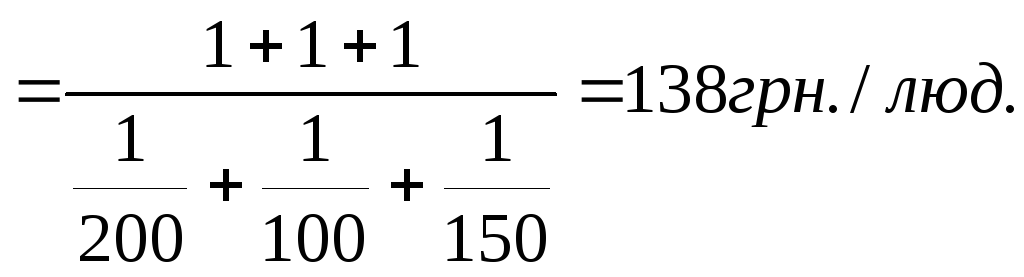
3. Середня квадратична

Застосовується для визначення середніх сторін квадратів, середніх діаметрів циліндричних тіл та ін.

Проста Зважена

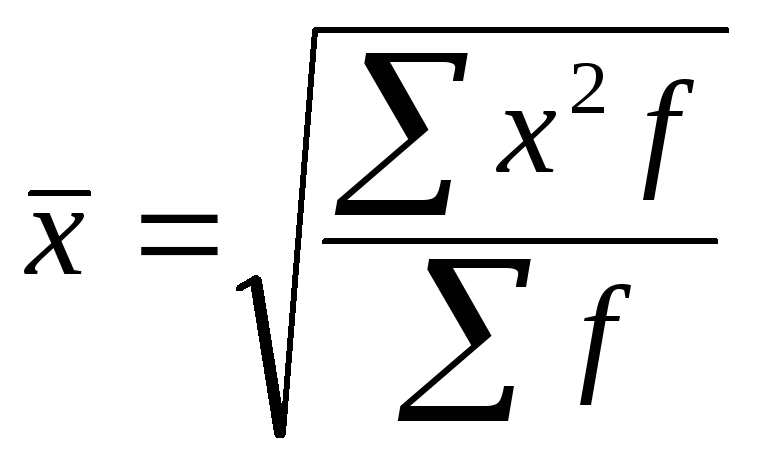
Позначення ті ж, що й у попередніх середніх.

ТИПОВА ЗАДАЧА

Є два квадрати зі сторонами 20 і 50 см. Визначити середню сторону квадрату.

Середня арифметична з цих величин - 35 см ( ) - помилковий результат.

Площа обох квадратів із такою стороною дорівнює 2450 см² (35²2), а справжня площа - 2900 см² (20² + 50²).

Знаючи площу двох квадратів (2900 см²) можна визначити сторону рівновеликого квадрата, вона буде дорівнювати кореню квадратному з половини загальної площі ( ) цей же результат дає і середня квадратична.

4. Структурні середні (мода, медіана).

Модою в статистиці називається ознака, що зустрічається в досліджуваній сукупності найбільш часто. Для дискретного ряду розподілу модою буде ознака, що має найбільшу частоту (наприклад: 160 грн./люд. , табл.8).

У інтервальних рядах розподілу моду визначають по формулі:

де Мо - мода;

х_о - початкове значення модального інтервалу

(інтервалу, що має найбільшу частоту ознаки);

i_Mo - величина модального інтервалу;

f_Mo - частота модального інтервалу;

f_Mo-1- частота інтервалу, що передує модальному;

f_Mo+1- частота інтервалу, наступного за модальним.

Медіаною, або серединною варіантою називається значення ознаки, що знаходиться в середині ряду значень, розташованих у порядку їхнього зростання або зменшення (ранжованний ряд розподілу).

Місце медіани у ранжованному ряду розподілу розраховується по формулі:

де N_Me номер (місце) медіани;

сума частот.

За даними табл.8 (ситуація 1):

таким чином 100 і 101 значення заробітної плати робітників є медіаною (160 грн./люд)

Медіана в інтервальному ряду розподілу розраховується по формулі:

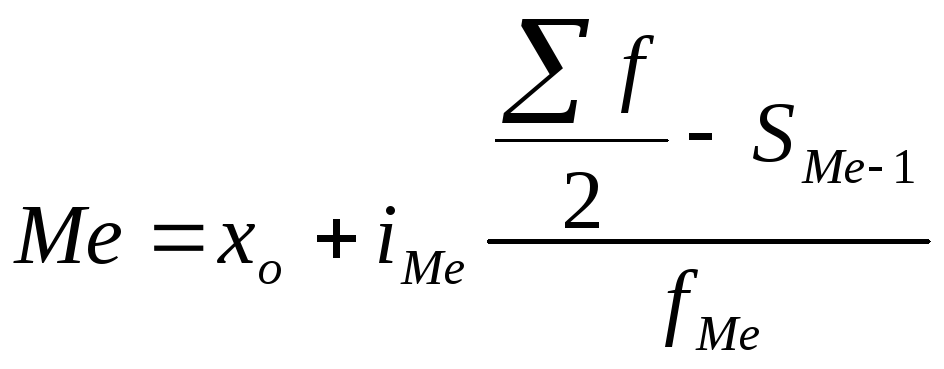
де x_o - початкове значення медіаного інтервалу (інтервал,

у якому знаходиться медіана);

i_Me - величина медіаного інтервалу ;

- полусума частот ;

S_Me-1- сума наростаючих (кумулятивних) частот,

що стоять перед медіаною частотою;

f_Me - частота медіаного інтервалу.

ТИПОВА ЗАДАЧА

За даними таблиці визначити моду і медіану:

Таблиця 10

Заробітна плата, грн./чол	Кількість робочих, чол.	Кумулятивна частота
100 - 120 120 - 140 140 - 160 160 - 180 180 - 200 200 - 220 220 - 240	10 20 55 40 50 20 15	10 30 (10+20=30) 85 (30+55=85) 125 (85+40=125) 175 (125+50=175) 195 (175+20=195) 210 (195+15=210)
Разом	210

Модальний інтервал - 140-160 грн./чол. (має найбільшу частоту ознаки).

Мода:

Номер медіани: (105, 106 робітник)

Медіаний інтервал - 160 - 180 грн./люд. (тому що заробітна плата 105 і 106 робітника знаходиться в інтервалі 160 - 180 грн./люд.

Медіана:

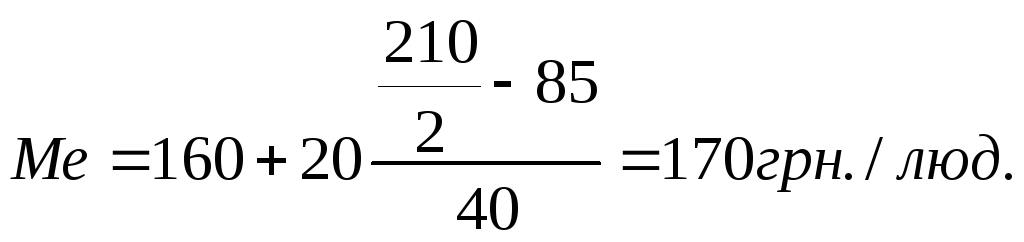
Крім медіани в ряду розподілу можна розрахувати квартилі (поділяють ранжованний ряд розподілу на чотири рівні частини), децілі (поділяють ряд на десять рівних частин).