
- •Глава 13 дифференциальные уравнения
- •§ 1. Обыкновенные дифференциальные уравнения
- •§ 2. Дифференциальные уравнения первого порядка
- •§ 3. Дифференциальные уравнения с разделяющимися переменными
- •§ 4. Дифференциальные уравнения однородные относительно переменных
- •§ 5. Линейные дифференциальные уравнения
- •§ 6. Дифференциальные уравнения второго порядка
- •§ 7. Уравнения второго порядка, допускающие понижение порядка
- •§ 8. Линейные дифференциальные уравнения второго порядка
- •§ 9. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- •§ 11. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Сводная таблица по теме: «Дифференциальные уравнения»
- •Решение практических задач
- •Примеры для самостоятельного решения.
Сводная таблица по теме: «Дифференциальные уравнения»
|
№ |
Вид уравнения |
Способ решения |
|
Дифференциальные уравнения первого порядка |
||
|
1. |
Уравнение с разделяющимися переменными X1 (x) Y1(y) d y + + X2(x)∙Y2 (y) d y = 0. |
а) X1 (x) Y1(y) d y = X2(x)∙Y2 (y) d y
б)
|
|
y = f1(x)∙f2(y). |
а)
б)
с)
|
|
|
2. |
Однородное
уравнение
|
а) Вводится замена
б) Получаем у = U x + U. в) подставляем в однородное уравнение: U x = f (U) – U.
в)
г) Интегрируя найдем:
|
|
3. |
Линейное уравнение у + р (х) у = f (x) |
а) Введем замену: у (х) = U (x) ∙ V (x), тогда у = U (x) ∙ V (x) + U (x) ∙ V (x). б) Получаем: U ∙V +U∙(V + p (x)∙V) = g (x).
в)
|
|
Дифференциальные уравнения второго порядка |
||
|
4. |
Допускающие понижение порядка: 1. у = f (x) не содержит явно у и у . |
а) Вводим замену у = р(х), у = р(х).
б)
в)
|
|
2. у = f (x, y ) не содержит явно у. |
а) Полагая у = р (х), у = р(х), т. е. р = f (x, p) б) р (х) = φ (х, С1). в) Интегрируем и получим
|
|
|
3. у = f (y, y ) не содержащим явно х |
а)
Полагая
у
= р
(у
(х)).
Тогда
б) Подставляя в уравнение получим р р = f (y, p).
в) Решая его,
найдем р =
φ (у, С1),
отсюда
г)
|
|
|
5. |
Линейное однородное уравнение у + р у + q y = 0 |
Составляем характеристическое уравнение: k2 + p k + q = 0.
Если k1
k2
, то
Если k1
= k2,
то
Если
|
|
6. |
Линейное неоднородное уравнение у + р у + q y = f (x). |
1. Решаем соответствующее однородное уравнение у + р у + q y = 0 2. По виду правой части уравнения записывается форма частного решения с неопределенными коэффициентами. 3. Таким образом сформированное частное решение подставляется в дифференциальное уравнение. 4. Из полученного тождества определяются значения коэффициентов.
5.
|
Решение практических задач
П р и м е р 1. Найти общий интеграл уравнения
![]() .
.
Решение. Разделим переменные в данном уравнении, поделив обе части на выражение cos2 y∙sin2 x:
![]() .
.
Интегрируя обе части данного уравнения, получим
![]() ,
,
откуда
![]()
Воспользуемся
тем, что С
– произвольная постоянная и заменим С
на
![]() .
Тогда
.
Тогда
![]() .
.
Это и есть общий интеграл данного уравнения.
П р и м е р 2. Найти общий интеграл уравнения
![]() .
.
Решение.
Разрешим уравнение относительно
производной
![]() :
:
![]() .
.
Поделив числитель и знаменатель правой части уравнения на х2, получим:
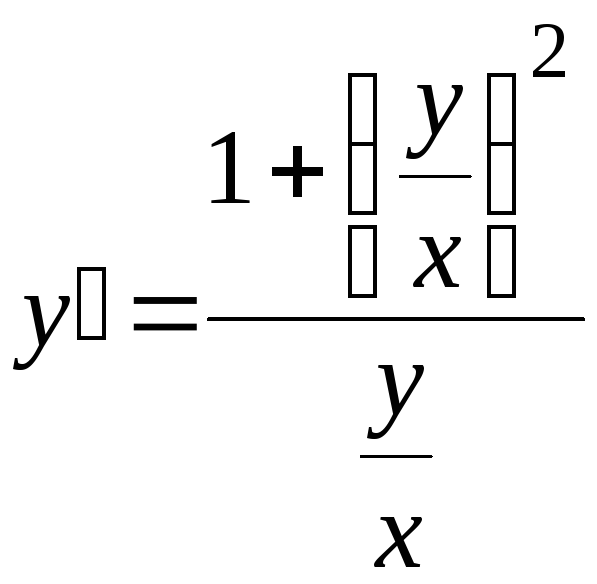
т. е. у
есть функция отношения
![]() .
Это означает, что данное уравнение –
однородное.
.
Это означает, что данное уравнение –
однородное.
Для решения этого
уравнения введем новую функцию
![]() .
Тогда у
= u
x
и
.
Тогда у
= u
x
и
![]() .
Тогда уравнение преобразуется в уравнение
с разделяющимися переменными:
.
Тогда уравнение преобразуется в уравнение
с разделяющимися переменными:
![]()
Интегрируя это уравнение, получим
![]() откуда
откуда
![]() .
.
Заменяя в последнем
равенстве U
отношением
![]() ,
окончательно получим:
,
окончательно получим:
![]() .
.
П р и м е р 3. Найти общее решение уравнения
![]() .
.
Решение. Положим y = u∙v, тогда y = u v + u v и данное уравнение примет вид:
![]() .
.
Решая уравнение
![]() ,
получим простейшее частное решение:
,
получим простейшее частное решение:
![]() .
.
Подставляя v в уравнение, получим
![]() .
.
из которого находим u:
![]()
Итак, искомое общее решение примет вид
![]()
П р и м е р 4. Найти общее решение уравнения
![]() .
.
Решение. 1) Найдем решение соответствующего однородного уравнения. Для этого составим характеристическое уравнение, т. е. y = k2, y = k:
![]() .
.
Следовательно,
![]() .
.
2) Найдем теперь
у*.
Здесь правая часть имеет вид
![]() ,
где k
= – 3, Pn(x)
= A.
Так как k
= – 3 является двукратным корнем
характеристического уравнения, т. е. r
= 2, то частное решение у*
следует искать в форме
,
где k
= – 3, Pn(x)
= A.
Так как k
= – 3 является двукратным корнем
характеристического уравнения, т. е. r
= 2, то частное решение у*
следует искать в форме
![]() ,
,
где А
– коэффициент, подлежащий определению.
Вычислим производные
![]() и
и
![]() :
:
![]() ;
;
![]() .
.
Подставляя выражения
для у*,
![]() и
и
![]() в данное выражение, сокращая обе части
на
в данное выражение, сокращая обе части
на
![]() и приводя подобные члены, в итоге получим
2 А
= 14, откуда А
= 7. Следовательно, искомое частное
решение имеет вид:
и приводя подобные члены, в итоге получим
2 А
= 14, откуда А
= 7. Следовательно, искомое частное
решение имеет вид:
![]()
Итак, общее решение данного уравнения
![]()

