§ 3. Дифференциальные уравнения с разделяющимися переменными

Определение 11. Дифференциальное уравнение вида

X (x) d x + Y (y) d y = 0 (5)

называется уравнением с разделенными переменными.

Считая y = φ(x) известной, это уравнение можно рассматривать как сумму двух дифференциалов, а неопределенные интегралы от них будут отличаться постоянным числом. То есть общий интеграл уравнения (5) имеет вид:

Определение 12. Уравнение вида

X₁(x) Y₁(y) d x + X₂(x) Y₂(y) d y = 0

называется уравнением с разделяющимися переменными.

Уравнение с разделяющимися переменными может быть приведено к уравнению (5) путем деления обеих частей уравнения на произведение Y₁(y)X₂(x):

Замечание. Уравнение у = f₁(x) f₂(y) приводится к уравнению (5) следующим образом

,

Решение f₂(y) = 0 может быть особым.

§ 4. Дифференциальные уравнения однородные относительно переменных

Определение 13. Функция f (x, y) называется однородной функцией п – го измерения относительно переменных х и у, если при любом k справедливо тождество: f (kx, ky) = k ⁿ f (x, y).

Замечание. Уравнение

М (х, у) d y + N (x,y) d x = 0

будет однородным в случае, если М (х, у), N (x, y)  однородные функции одного и того же измерения.

Определение 14. Функция f (x, y) называется однородной функцией нулевого измерения, если при умножении аргументов х и у на произвольный параметр k значение функции не измениться: f (k_x, k_y)= f(x,y).

Определение 15. Уравнением однородным, относительно переменных называется уравнение вида:

При решении однородного уравнения вводится замена

, т. е. y = U∙x,

тогда у = U x + U, подставляя это выражение для у в однородное уравнение, получим:

U x + U = f (U)

или U x = f (U) – U  это уравнение с разделяющимися переменными:

Интегрируя найдем:

Подставляя после интегрирования вместо U отношение , получим интеграл однородного уравнения.

К однородным уравнениям приводятся уравнения вида

Это достигается линейной заменой x = x₀ + t, y = y₀ + z, где х₀, у₀  координаты точки пересечения прямых а₁ х + b₁ y + c₁ = 0 и a₂ x + b₂ y + c₂ = 0. Если же указанные прямые не пересекаются, то в этом случае и уравнение приводится к уравнению с разделяющимися переменными с помощью замены а₁х+b₁y+c₁=z.

§ 5. Линейные дифференциальные уравнения

Определение 16. Уравнение вида

у + р (х) у = f (x), (6)

где р (х) и f (x)  непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Если f (x)  0, то уравнение (6) называется линейным однородным уравнением. Если f (x)  0, то уравнение (6) называется линейным неоднородным дифференциальным уравнением.

Для нахождения общего решения уравнения (6) можно пользоваться следующим способом.

Будем искать решение у (х) уравнения (6) в виде

у (х) = U (x) ∙ V (x), (7)

где U (x) и V (x) – неизвестные функции, одна из которых, например V (x), может быть выбрана произвольно. Подставляя у (х) в форме (7) в уравнение (6), учитывая, что у  = U  (x) ∙ V (x) + U (x) ∙ V  (x):

U ∙V + U∙V  + p (x)∙U∙V = g (x).

После элементарных преобразований получим

U ∙V + U∙(V  + p (x)∙V) = g (x).

Выберем в качестве V (x) любое частное решение V (x)  0 уравнения

V  + p (x)∙V = 0,

Тогда U ∙V = g (x).

Итак, решение уравнения (5) сводится к решению системы дифференциальных уравнений (сначала решается первое уравнение, затем второе)

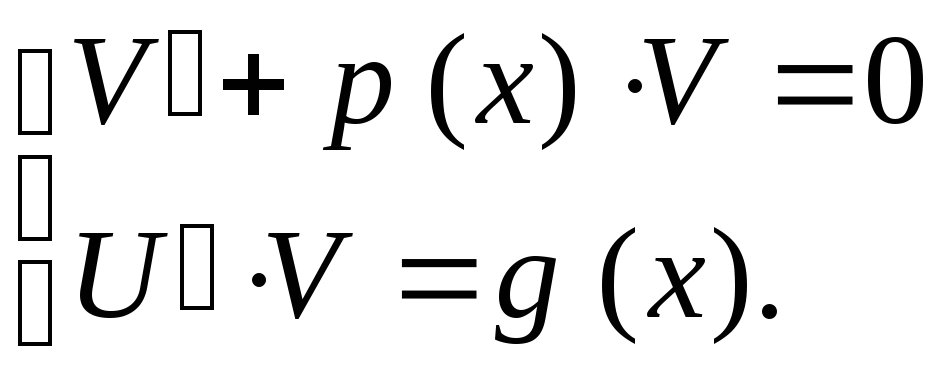
Зная U (x) и V (x), найдем решение у (х) по формуле (7) уравнения (6).