Решение практических задач по теме: «Раскрытие некоторых неопределенностей»
П р и м е р 1.
Найти
.
Решение. Чтобы вычислить предел надо подставить в данную функцию предельное значение х = 1, т. е.:
.
П р и м е р 2.
Найти
.
Решение.
Подставим в данную функцию предельное
значение х
= 3 и получим неопределенность вида
.
Так как и в числителе и в знаменателе
стоят многочлены, то, чтобы разрешить
эту неопределенность, разделим и
числитель и знаменатель на (х
– 3), т. е.:
.
П р и м е р 3.
Найти
.
Решение.
Подставим в данную функцию предельное
значение х
= 1 и получим неопределенность вида
.
Так как и в числителе и в знаменателе
стоят многочлены второй степени, то,
чтобы разрешить эту неопределенность,
представим и числитель и знаменатель
в виде произведений, т. е.:
;
.
Тогда предел запишется в виде:
.
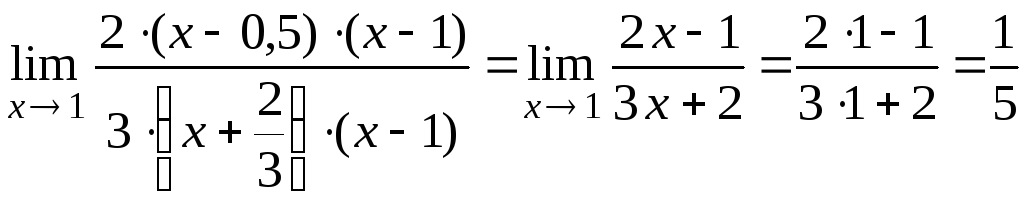П р и м е р 4.
Найти
.
Решение.
Подставим в данную функцию предельное
значение х
= 5 и получим неопределенность вида
.
Так как числитель – это иррациональная
функция, то, чтобы разрешить эту
неопределенность, домножим и числитель,
и знаменатель на выражение сопряженное
числителю, т. е. на
:
.
П р и м е р 5.
Найти
.
Решение.
Подставим в данную функцию предельное
значение х
=
и получим неопределенность вида
.
Так как в числителе и в знаменателе
стоят многочлены третьей степени, то,
чтобы разрешить эту неопределенность,
разделим и числитель, и знаменатель на
х
в наибольшей степени, т. е. на х3:
,
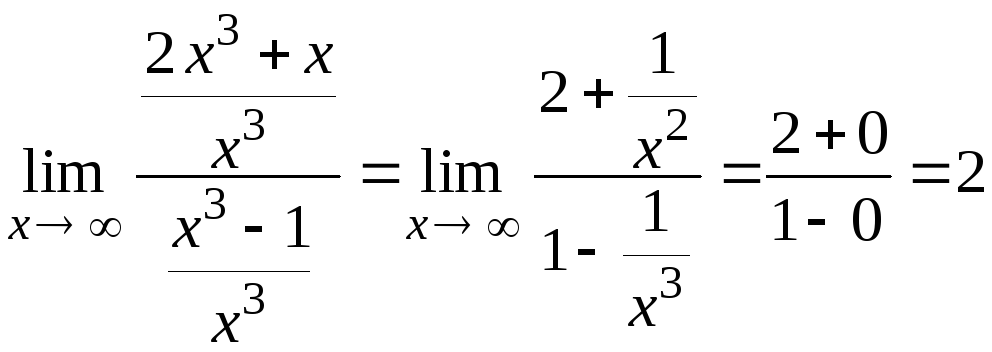так как при х
дроби
и
стремятся к нулю.
П р и м е р 6.
Найти
.
Решение.
Подставим в данную функцию предельное
значение х
=
и получим неопределенность вида
.
Так как в числителе и в знаменателе
стоят иррациональные функции, то, чтобы
разрешить эту неопределенность, разделим
и числитель, и знаменатель на х
в наибольшей степени. Для этого сравним
отдельно степени х,
т. е.:
и
.
Так как
больше чем
,
то будем делить на
:
,
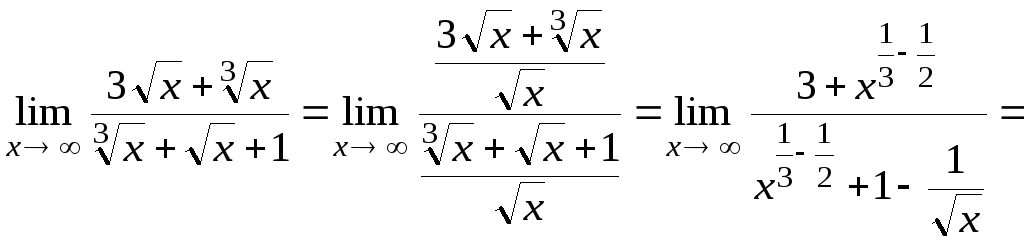
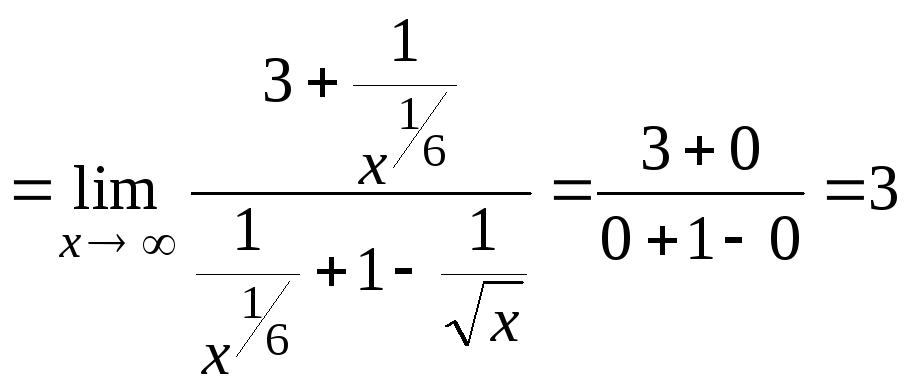так как при х
дроби
и
стремятся к нулю.
Решение практических задач по теме: «Замечательные пределы»
П р и м е р 7.
Найти
.
Решение.
Подставив в функцию предельное значение
х
= 0, получаем неопределенность вида
.
Так как в функции присутствует
тригонометрическая зависимость, то
воспользуемся первым замечательным
пределом, т. е.:
.
П р и м е р 8.
Найти
.
Решение.
Подставив в функцию предельное значение
х
= 0, получаем неопределенность вида
.
Так как в функции присутствует
тригонометрическая зависимость, то
сведем данную функцию к первому
замечательному пределу, т. е.:
.
П р и м е р 9.
Найти
.
Решение.
Подставив в функцию предельное значение
х
= ,
получаем неопределенность вида
.
Сведем данную функцию ко второму
замечательному пределу, т. е. выделим
целую часть в скобках:
.
Обозначим
,
откуда
.
Причем при х
t
0. Следовательно,
.
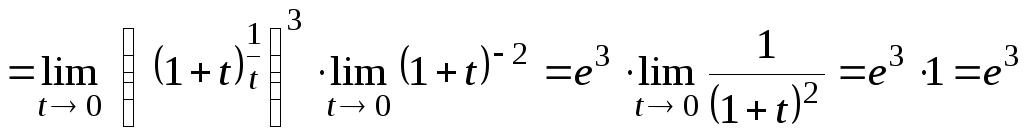Решение практических задач по теме:
«Эквивалентные бесконечно малые функции»
П р и м е р 10.
Найти
.
Решение. Воспользуемся таблицей эквивалентных функций и заменим arctg 2 x 2 x. Тогда
.
П р и м е р 11.
Найти
.
Решение.
Воспользуемся таблицей эквивалентных
функций и заменим
.
Тогда
.
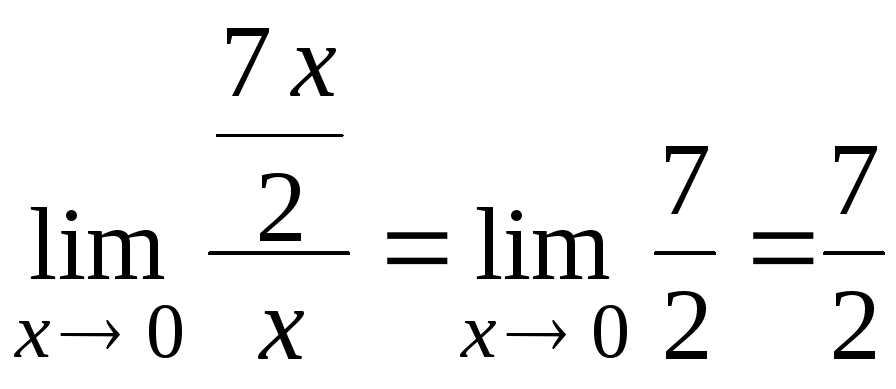П р и м е р 12.
Найти
.
Решение.
Воспользуемся таблицей эквивалентных
функций и заменим (еx
– 1)
x
и (1 – cos
x)
.
Тогда
.
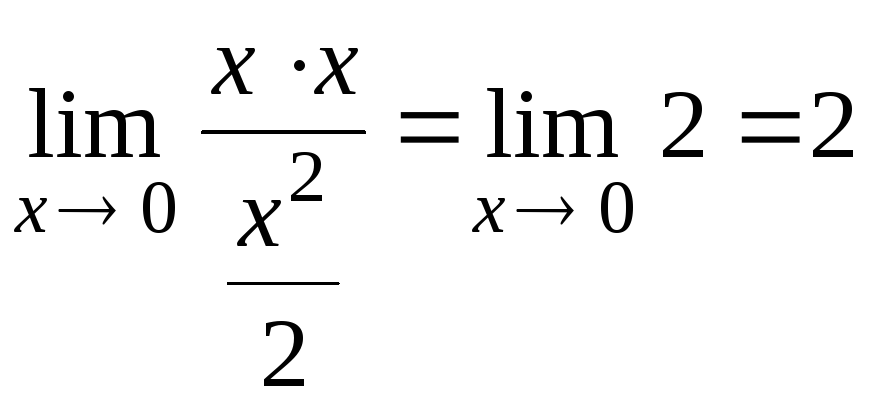Решение практических задач по теме:
«Непрерывность функции»
П р и м е р 13.
Исследовать на непрерывность функцию
.
Решение. Очевидно, что функция непрерывна при х 3. Найдем односторонние пределы в этих точках. Сначала найдем предел слева для точки х = 3:
Аналогично найдем предел справа для точки х = 3, т. е.
Следовательно, х = 3 – точка разрыва второго рода.
Теперь найдем предел слева для точки х = – 3:
Аналогично найдем предел справа для точки х = – 3, т. е.
Следовательно, х = – 3 – точка разрыва второго рода.