§ 8. Замечательные пределы

Первый замечательный предел (неопределенность типа ).

, где угол х измеряется в радианах.

Второй замечательный предел (неопределенность типа 1^).

, где е = 2,7183… – иррациональное число

или .

Другие важные пределы:

1)

2)

3)

§ 9. Непрерывность функции

Пусть функция у = f (x) определена при некотором значении х₀ и в некоторой ее окрестности. Пусть у₀ = f (x₀). Если х получит некоторое положительное или отрицательное приращение ∆х и примет значение х = х₀ + ∆х, то функция у получит некоторое приращение ∆у. Новое, наращенное значение функции будет у₀ + ∆у = f (x₀ + ∆x). Тогда приращение функции определяется формулой

∆у = f (x₀ + ∆x) – f (x₀).

О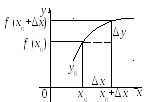пределение 31. Функция у = f (x) называется непрерывной в точке х₀, если она определена в этой точке и ее окрестности и если , т. е. если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, или что то же самое,

.

Приведем еще одно определение непрерывной в точке функции.

Определение 32. Функция f (x) называется непрерывной в точке х₀, если:

1. Эта функция определена в точке х₀ и некоторой ее окрестности;

2. Имеет место равенство , т. е. когда предел функции при х → х₀ равен значению функции в предельной точке.

Определение 33. Функция, непрерывная в каждой точке некоторого отрезка, называется непрерывной на этом отрезке.

Определение 34. Если условие непрерывности функции в точке х₀ не выполняется, то функция называется разрывной в этой точке, а сама точка х₀ называется точкой разрыва функции у = f (x).

Т е о р е м а 16. Функция f (x) непрерывная при х₀ тогда и только тогда, когда выполняется соотношение:

или в других обозначениях

f (x₀ – 0) = f (x₀ + 0) = f (x₀). (2)

Классификация точек разрыва функции.

Определение 35. Если существуют конечные пределы f (x₀ – 0) и f (x₀ + 0), но не выполнено хотя бы одно из равенств (6), то точка х₀ называется точкой разрыва первого рода. Если при этом еще

f (x₀ – 0) = f (x₀ + 0)  f (x₀),

то точка х₀ называется устранимой точкой разрыва (достаточно изменить значение f (x) в одной точке, положив f (x₀ + 0) = f (x₀), как функция станет непрерывной). Если же в точке х₀ не существует или бесконечен хотя бы один из односторонних пределов, то точка х₀ называется точкой разрыва второго рода.

Т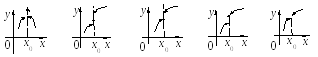очки разрыва первого рода.

Точки разрыва второго рода.

Операции над непрерывными функциями.

Т е о р е м а 17. Если функции f (x) и g (x) непрерывны в точке х₀, то их сумма, произведение также непрерывны в точке х₀. Если, кроме того, g (x)  0, то функция непрерывна в точке х₀.

Т е о р е м а 18. Если функция U = φ (x) непрерывна в точке х₀ и f (U) непрерывна в точке U₀ = φ (х₀), то сложная функция f (φ(x)) непрерывна в точке х₀.

Т е о р е м а 19. Всякая элементарная функция непрерывна в каждой точке области своего существования.

Свойства функций непрерывных на отрезке.

Т е о р е м а 20. Если функция f (x) непрерывна на отрезке [a; b], то она достигает на этом отрезке своего наибольшего и наименьшего значений.

Г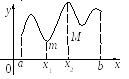еометрическое истолкование. Эта теорема утверждает, что на отрезке [a; b] найдутся такие точки х₁, х₂, что значение функции f (x) в этих точках является f (x₁) – наименьшим, f (x₂) – наибольшим из всех значений функции на отрезке:

f (x₁)  f (x) f (x)  f (x₂).

Замечание. Утверждение теоремы становится неверным на (a; b). Например, у = х непрерывная на (0; 1) не достигает на этом интервале наибольшего и наименьшего значений. Она принимает значение, сколь угодно близкое к 1 и 0 (так как 0 и 1 не принадлежат этому интервалу).

Следствие. Если f (x) непрерывна на отрезке, то она ограничена на этом отрезке.

Т е о р е м а 21. Если функция y = f (x) непрерывна на отрезке [a; b] и на его концах принимает значения разных знаков, то внутри этого отрезка найдется, по крайней мере, одна точка, в которой функция равна нулю.

Если точки графика y = f (x), соответствующие концам отрезка [a; b], лежат по разные стороны от оси Ох, то этот график хотя бы в одной точке отрезка пересекает ось Ох.

Т е о р е м а 22. (о промежуточных значениях). Пусть функция y = f (x) непрерывна на отрезке [a; b] и f (a) = А, f (b) = В. Тогда для любого числа С, заключенного между А и В, найдется внутри отрезка [a; b] такая точка с, что f (c) = C.

Прямая у = С пересечет график функции f (x) по крайней мере в одной точке. Таким образом, непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.

Т е о р е м а 23. (о существовании обратной непрерывной функции). Если функция непрерывна на отрезке [a; b] и является монотонной на нем, то обратная функция на соответствующем отрезке [f (a); f (b)] оси Оу существует и является также непрерывной и монотонной на этом отрезке.