
- •Глава 6 ведение в анализ
- •§ 1. Функция одной переменной
- •§ 2. Модуль действительного числа
- •§ 3. Предел функции одной переменной
- •§ 4. Бесконечно большой аргумент и функция
- •§ 5. Бесконечно малые функции (б. М. Ф.)
- •Свойства бесконечно малой функции.
- •§ 6. Сравнение бесконечно малых функций
- •§ 7. Основные теоремы о пределах
- •§ 8. Замечательные пределы
- •§ 9. Непрерывность функции
- •Решение практических задач по теме: «Раскрытие некоторых неопределенностей»
- •Решение практических задач по теме: «Замечательные пределы»
- •Примеры для самостоятельного решения.
§ 6. Сравнение бесконечно малых функций
Пусть α (х) и β (х) – б. м. ф. при х х0.
Определение 27.
Если
![]() ,
то α (х)
называется бесконечно
малой функцией более высокого порядка,
чем β (х).
,
то α (х)
называется бесконечно
малой функцией более высокого порядка,
чем β (х).
Так α
(х)
= х2
– б. м. ф. при х
0 более высокого порядка, чем β (х)
= х
при х
0, т. к.
![]() .
.
Определение 28.
Если
![]() ,
то α (х)
и β (х)
называются бесконечно
малыми функциями одного порядка.
Так α (х)
= 2 х,
β (х)
= х,
при х
0 – б. м. ф. одного порядка, т. к.
,
то α (х)
и β (х)
называются бесконечно
малыми функциями одного порядка.
Так α (х)
= 2 х,
β (х)
= х,
при х
0 – б. м. ф. одного порядка, т. к.
![]() .
.
Определение 29.
Говорят, что б. м. ф. α (х)
и β (х)
при х
х0
не сравнимы,
если отношение
![]() при х
х0
не имеют предела, ни конечного, ни
бесконечного.
при х
х0
не имеют предела, ни конечного, ни
бесконечного.
Например, б. м. при
х
0 функция
![]() и β (х)
= х
не сравнимы, т. к. их отношение
и β (х)
= х
не сравнимы, т. к. их отношение
![]() не имеет конечного предела в точке х
= 0 и не является б. б. ф. при х
0.
не имеет конечного предела в точке х
= 0 и не является б. б. ф. при х
0.
Определение 30. Две б. м. ф. α (х) и β (х) при х х0 называются эквивалентными, если предел их отношения равен единице:
![]() .
.
Эквивалентные б. м. ф. представляют частный случай б. м. одного порядка. Эквивалентность б. м. ф. α (х) и β (х) обозначается следующим образом:
α (х) β (х), при х х0.
Т е о р е м а 3. Предел отношения двух б. м. ф. при х → х0 не изменяется, если каждую или одну из них заменить эквивалентной ей б. м. ф. при х → х0.
Замечание. Пусть α (х), β (х), γ (х) – б. м. ф. при х х0 отношение эквивалентности обладает свойством
– рефлективности: α (х) α(х), при х х0;
– симметричности: если α (х) β (х), то β (х) α (х), при х х0;
– транзитивности: если α (х) β (х), а β (х) γ (х), то α (х) γ (х), при х х0.
Таблица эквивалентных бесконечно малых функций при х 0
|
sin x x |
ln (1 + x) x |
|
|
tg x x |
ax – 1 x∙ln a |
|
|
|
ex – 1 x |
|
|
arcsin x x |
log a (1 + x) x∙log a e |
|
|
arctg x x |
§ 7. Основные теоремы о пределах
Для определенности все доказательства и формулировки проведем для х → + х0. Теоремы для случаев: х → – , х → + , х → х0 0 совершенно аналогичны.
Т е о р е м а 4.
(прямая)
(о
связи между функцией, имеющей предел,
и б. м. ф.).
Если функция f
(x)
имеет предел (при х
→ х0)
равный А,
то ее можно представить как сумму числа
А
и б. м. ф. (при х
→ х0),
т. е. если
![]() ,
то
,
то
f (x) = A + α (x), где α (х) – б. м. ф. при х → . (1)
Т е о р е м а 5. (обратная). Если функцию f (x) можно представить как сумму числа А и некоторой б. м. ф. (х → х0), т. е. f (x) = A + α (x), то число А является пределом функции f (x) при х → х0.
Т е о р е м а 6. Если функция y = f (x) имеет предел при х → х0, то она ограничена своим пределом в некоторой окрестности этой точки.
Т е о р е м а 7. (о пределе постоянной функции). Предел постоянной при х → + х0 равен самой этой постоянной.
![]() где С
= const.
где С
= const.
Т е о р е м а 8. (о пределе суммы функций, имеющих предел). Предел суммы (разности) двух функций равен сумме (разности) их пределов, т. е. если
![]() и
и
![]() ,
то
,
то
![]()
Примечание. Теорема 7 справедлива для алгебраической суммы любого конечного числа функций.
Т е о р е м а 9. (о пределе произведения функций, имеющих пределы). Предел произведения двух функций равен произведению их пределов, т. е. если существуют
![]() и
и
![]() ,
то
,
то
![]() .
.
Следствие 1. Постоянный множитель можно выносить за знак предела, т.е.
![]()
Примечание. Теорема 8 справедлива для любого конечного числа сомножителей.
Следствие 2. Предел степени равен степени предела, т. е.
![]() .
.
Т е о р е м а 10. (о пределе частного). Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю, т.е.
![]() ,
,
![]() ,
то
,
то
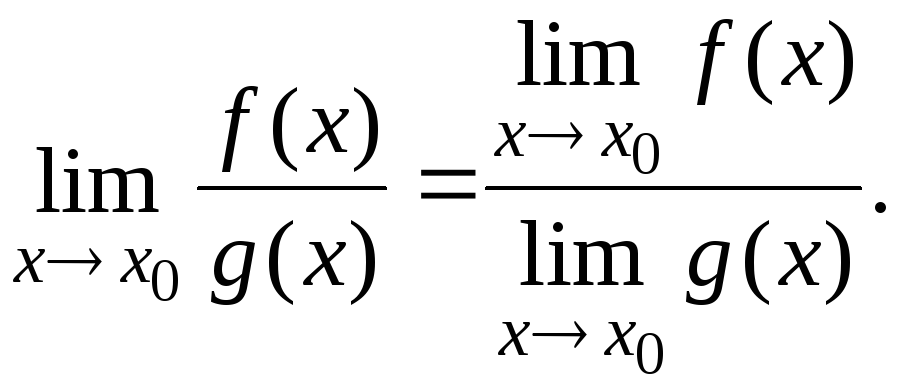
Примечание. Теоремы о пределах суммы, произведения и частного облегчают нахождения пределов.
Т е о р е м а 11.Если f (x) 0 в окрестности точки х0 и при х→ х0 имеет предел, то этот предел не может быть отрицательным, т. е.
![]() .
.
Т е о р е м а 12 (переход к пределу в неравенстве). Если f (x) g (x) для всех х из некоторой окрестности точки х0, кроме, быть может, самой точки х0, и каждая из функций f (x) и g (x) в точке х0 имеет предел, то
![]() .
.
Т е о р е м а 13. (о пределе промежуточной функции). Пусть три функции φ (х), f (x), g (x) удовлетворяют неравенствам
φ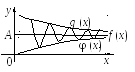 (x)
f
(x)
g
(x)
для х
→ х0.
(x)
f
(x)
g
(x)
для х
→ х0.
Тогда, если
![]() ,
то и f
(x)
имеет предел, равный А:
,
то и f
(x)
имеет предел, равный А:
![]() .
.
Т е о р е м а 14. Предел логарифма функции равен логарифму ее предела, т. е.
![]()
Т е о р е м а 15.
Если
![]() существует, то
существует, то
![]()
Раскрытие некоторых неопределенностей
Раскрытие
неопределенностей − это методы вычисления
пределов функций, заданных формулами,
которые в результате формальной
подстановки в них предельных значений
аргумента теряют смысл, т. е. переходят
в выражения (неопределенности) типа
![]() ,
по которым нельзя судить о том, существуют
или нет искомые пределы.
,
по которым нельзя судить о том, существуют
или нет искомые пределы.
Рассмотрим дробную рациональную функцию, т. е. отношение двух многочленов
 .
.
1. Пусть х → а.
Если
![]() ,
то
,
то
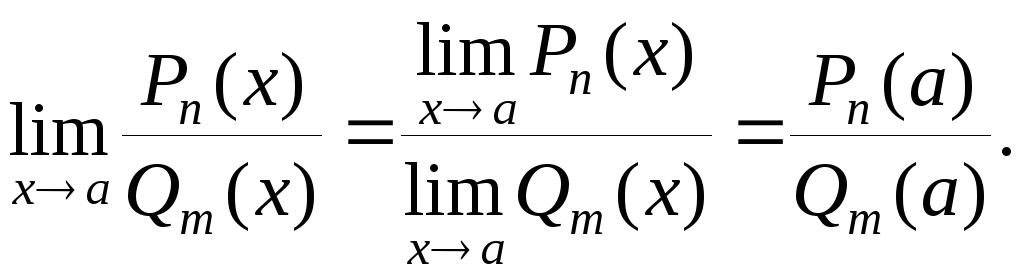
Если Рn(a)
0, Qm(a)
= 0, то
![]() .
.
Если Рn(a)
= 0, Qm(a)
= 0, получим неопределенность
![]() .
Для того, чтобы раскрыть эту неопределенность,
необходимо выделить критический
множитель (т. е. множитель равный нулю
при х
= а)
(х – а)
и сократить дробь
.
Для того, чтобы раскрыть эту неопределенность,
необходимо выделить критический
множитель (т. е. множитель равный нулю
при х
= а)
(х – а)
и сократить дробь
![]() один или несколько раз на этот множитель.
один или несколько раз на этот множитель.
2.
Пусть х
и
![]() и
и
![]() .
Получим неопределенность
.
Получим неопределенность
![]() .
В этом случае надо и числитель и
знаменатель дроби разделить на старший
член числителя
.
В этом случае надо и числитель и
знаменатель дроби разделить на старший
член числителя
![]() или знаменателя
или знаменателя
![]() .
В результате получим
.
В результате получим
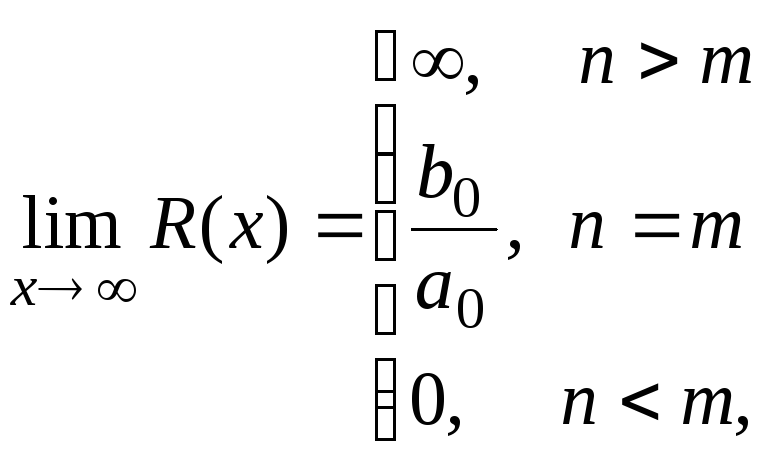
т. е. предел дробной рациональной функции при х → равен отношению коэффициентов при старших членах, если степени числителя и знаменателя одинаковы, и равен нулю или бесконечности, если степень числителя соответственно меньше или больше степени знаменателя.
3.
Выражения, содержащие иррациональности
в числителе и знаменателе и дающие
неопределенность вида
![]() ,
приводятся к рациональному виду во
многих случаях путем введения новой
переменной.
,
приводятся к рациональному виду во
многих случаях путем введения новой
переменной.
Другим приемом нахождения предела от иррационального выражения является перевод иррациональности из числителя в знаменатель или, наоборот, из знаменателя в числитель.
4.
При нахождении пределов могут встретиться
неопределенности вида
–
и 0∙.
Каждый из этих случаев путем преобразования
данной функции можно привести к
неопределенности вида
![]() или
или
![]() .
.
