§ 4. Бесконечно большой аргумент и функция

Определение 21. Функция f (x) называется ограниченной в данной области изменения аргумента х, если существует положительное число М такое, что для всех значений х, принадлежащих рассматриваемой области, будет выполняться неравенство | f (x)|  M. Если же такого числа М не существует, то функция f (x) называется неограниченной в данной области.

Определение 22. Если х неограниченно возрастает, т. е. может стать больше как угодно большого наперед заданного числа М > 0, т. е. x > M, или если х неограниченно убывает, т. е. может стать меньше любого наперед заданного числа x < – M (M > 0), то пишут х → +  и х → –  соответственно, и говорят, что х бесконечно большой аргумент.

Определение 23. Функция f (x) называется бесконечно большой при х → х₀, если для каждого положительного числа М, как бы велико оно ни было, можно найти такое δ > 0, что для всех значений х, отличных от х₀, удовлетворяющих условию |x – x₀| < δ, имеет место неравенство | f (x)| > M, т. е.:

М > 0 δ > 0 x  х₀: |x – x₀| < δ  | f (x) | > М.

Если f (x) стремится к  при х → х₀ и при этом принимает только положительные или только отрицательные значения, соответственно пишут

или .

Дадим теперь точное определение предела функции при х → + .

Определение 24. Число А называется пределом функции f (x) при х → + (х → – ),если каково бы ни было положительное число ε, можно найти такое число N > 0, что для всех х > N (х < – N), выполняется неравенство

| f (x) – A| < ε.

Обозначается

Символическая запись:

ε > 0 N > 0 x > N (х < – N) | f (x) – A| < ε.

Функция, стремящаяся к пределу, может оставаться все время меньше его, или больше его, и, наконец, может колебаться около него.

Например,

Ч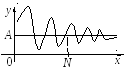исло N, вообще говоря, зависит от ε. Чем меньше ε, т. е. чем уже полоса между прямыми у = А – ε и у = А + ε, тем большим будет N.

О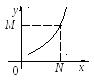пределение 25. Функция f (x) называется бесконечно большой при бесконечно большом аргументе, если каково бы ни было М > 0, можно найти такое число N > 0, что для всех |x| > N выполняется неравенство | f (x)| > M.

Обозначается

, ,

, .

Символическая запись:

М > 0 N > 0 x: |x | > N  | f (x) | > М.

§ 5. Бесконечно малые функции (б. М. Ф.)

Определение 26. Функция  (x) называется бесконечно малой функцией при х → х₀, если .

Если или , то функция  (x) называется бесконечно малой соответственно при х → +  или при х → − .

Обозначаются бесконечно малые функции буквами греческого алфавита  (x),  (x),  (x), 

Замечание: Далее будем рассматривать бесконечно малые функции, определенные в некоторой окрестности точки х₀, за исключением быть может самой точки х₀. Точка х₀ может быть конечной или бесконечно удаленной (+, − , ).

Свойства бесконечно малой функции.

1. Сумма конечного числа б. м. ф. при х → х₀ есть функция бесконечно малая при х → х₀.

2. Произведение б. м. ф. при х → х₀ на функцию ограниченную в окрестности точки х₀, является функцией бесконечно малой при х → х₀.

С л е д с т в и е 1. Произведение двух б. м. ф. при х → х₀ есть б. м. ф. при х → х₀

С л е д с т в и е 2. Произведение б. м. ф. при х → х₀ на число есть б. м. ф. при х → х₀.

3. Если α (х) − б. м. ф. при х → х₀ , а функция φ (х) имеет в точке х₀ предел, отличный от нуля, то частное есть б. м. ф. при х → х₀.

Связь бесконечно малой функции с бесконечно большой функцией.

Т е о р е м а 1. Если функция f (x) является бесконечно большой (б. б. ф.) при х → х₀, то функция – б. м. ф. для тех же х.

Т е о р е м а 2. Если функция α (х) – б. м. ф. при х → х₀ не обращающаяся в ноль, то – б. б. ф. для тех же х.