§ 2. Модуль действительного числа

Определение 15. Модулем (или абсолютной величиной) действительного числа х называется неотрицательное число, обозначаемое |x| и определяемое формулой

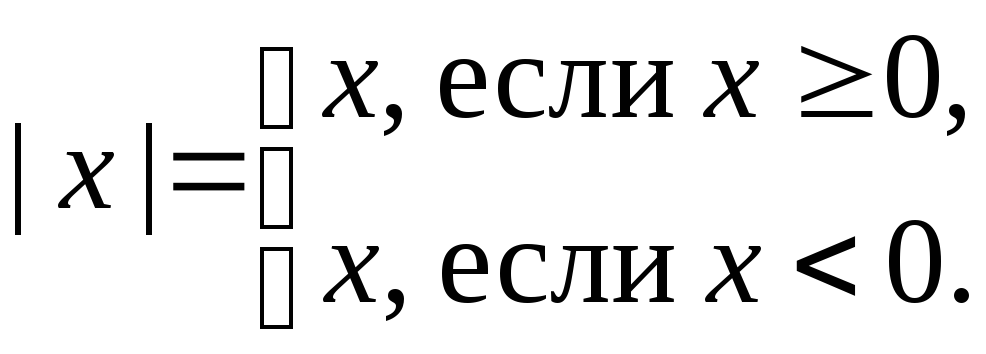
Из определения следует, что для всех х справедливо соотношение .

Е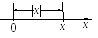сли расположить действительные числа на числовой оси, то модуль |x| любого числа х представляет собой расстояние от начала отсчета О до соответствующей точки с абсциссой х.

Отсюда следует, что если модуль числа х удовлетворяет неравенству

|x| < a (или |x| ≤ a), где a > 0,

то число х подчинено ограничению:

– a < x < a (или соответственно – a ≤ x ≤ a)

т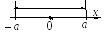. е. х принадлежит интервалу (– а; а) (или отрезку [– а; а]).

Рассмотрим более общий случай:

если |x – х₀| < a (или | x – х₀| ≤ a),то число х подчинено ограничению:

х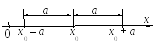₀ – a < x < х₀ + a (или соответственно х₀ – a ≤ x ≤ х₀ + a),

т. е. х принадлежит интервалу с центром в точке х_0- (х₀ – а; х₀ + а) (или отрезку [х₀ – а; х₀ + а]).

Свойства модуля действительного числа.

1. |x + y| ≤ |x| + |y|. Неравенство распространяется на любое конечное число слагаемых.

2. |x – y| ≥ |x| – |y|.

3. |x∙y| = |x|∙|y|. Равенство распространяется на любое конечное число сомножителей.

4. .

5. |xⁿ| = |x|ⁿ.

§ 3. Предел функции одной переменной

Определение 16. Постоянное число х₀ называется пределом переменной величины х в данном процессе, если для каждого наперед заданного произвольно малого δ > 0 можно указать такое значение переменной х, что все последующие значения переменной будут удовлетворять неравенству

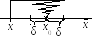
Если число х₀ есть предел переменной величины х, то говорят, что х стремится к пределу х₀, и пишут:

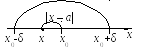или

С помощью логических символов это определение выражается следующим образом

.

Е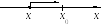сли х → х₀, х < х₀, то говорят, что х стремиться к х₀ слева и пишут: х → х₀ – 0.

Е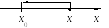сли х → х₀, х > х₀, то говорят, что х стремиться к х₀ справа и пишут: х → х₀ + 0.

Определение 17. (предела функции при х → х₀ – 0). Число А называется пределом функции f (x) при х → х₀ – 0, если каково бы ни было положительное число ε, найдется такое δ, что для всех х ∈ (х₀ – δ; х₀) выполняется неравенство

| f (x) – A| < ε.

Обозначается

Символическая запись:

ε > 0 δ > 0 x: х₀ – δ < x < x₀  | f (x) – A| < ε.

Г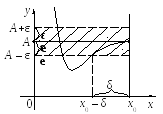еометрический смысл предела функции при х → х₀ – 0 заключается в следующем: каково бы ни было ε > 0 найдется такое δ > 0, что для всех х заключенных между х₀ – δ и х₀, график функции лежит в полосе, ограниченной прямыми у = А – ε и у = А+ ε.

Аналогично пределу функции при х → х₀ – 0 вводится понятие предела при х → х₀ + 0.

Определение 18. Число А называется пределом функции f (x) при х → х₀+0, если каково бы ни было число ε, найдется такое δ > 0, что для всех х  (х₀; x₀ + δ), выполняется неравенство | f (x) – A| < ε,

Обозначается

Символическая запись:

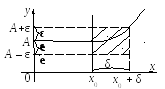ε > 0 δ > 0 x: x₀ < x < x₀+δ  | f (x) – A| < ε.

Геометрически это означает, что график функции лежит в полосе, ограниченной прямыми у = А – ε и у = А+ ε для всех х, заключенных между х₀ и x₀ + δ.

Пределы функции при х → х₀ – 0 и х → х₀ + 0 называются односторонними пределами.

Если оба односторонних предела существуют и равны между собой, то говорят, что f (x) имеет двусторонний предел при х → х₀, или просто имеет предел при х → х₀

О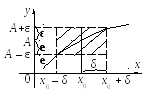пределение 19. Число А называется пределом f (x) при х → х₀, если каково бы ни было ε > 0, можно найти такое δ, что для всех х ∈ (х₀ – δ; х₀+δ) (за исключением быть может точки х₀), выполняется неравенство

| f (x) – A| < ε,

Обозначается

Символическая запись:

ε > 0 δ > 0 x: 0 < |x – x₀| < δ  | f (x) – A| < ε.

Геометрически это значит, что для всех точек х, отстоящих от точки х₀ не далее чем на δ, точки графика функции f (x) лежат внутри полосы шириной 2ε, ограниченной прямыми у = А – ε и у = А+ ε.

Определение 20. Назовем окрестностью точки х₀ любой интервал, содержащий эту точку. Дельта – окрестностью (δ –окрестностью) точки х₀ называется интервал х₀ – δ < х₀ < х₀ + δ.