
- •Глава 5 Аналитическая геометрия в пространстве
- •§ 1. Плоскость
- •1. Угол между плоскостями.
- •2. Условие перпендикулярности двух плоскостей
- •3. Условие параллельности двух плоскостей
- •4. Условие совпадения плоскостей
- •§ 2. Прямая в пространстве
- •§ 3. Прямая и плоскость в пространстве
- •§4. Поверхности второго порядка
- •§ 4.1. Цилиндры второго порядка
- •§ 4.2. Эллипсоид, конус, гиперболоид
- •§ 4.3. Параболоиды.
- •«Прямая и плоскость в пространстве»
- •Решение практических задач по теме: «Плоскость»
- •Решение практических задач по теме: «Прямая в пространстве. Взаимное расположение прямой и плоскости»
- •Решение практических задач по теме: «Поверхности второго порядка»
- •Примеры для самостоятельного решения
Решение практических задач по теме: «Поверхности второго порядка»
П р и м е р 13.
Определить и построить цилиндр:
![]() .
.
Р ешение.
Так как две переменные в квадратах и
все коэффициенты положительные, то
делаем вывод, что данная поверхность –
это эллиптический цилиндр с образующими
параллельными оси Ох
и направляющей – эллипсом
ешение.
Так как две переменные в квадратах и
все коэффициенты положительные, то
делаем вывод, что данная поверхность –
это эллиптический цилиндр с образующими
параллельными оси Ох
и направляющей – эллипсом
![]() в плоскости уОz.
в плоскости уОz.
В плоскости уОz строим эллипс с полуосями b = 5, c = 2. Затем строим такой же эллипс в любой плоскости x = h и параллельно оси Ох проводим образующие. Поверхность является неограниченной, на рисунке изображена лишь часть ее.
П р и м е р 14.
Определить и построить поверхность:
![]()
Решение. Так как все переменные в квадратах и один из коэффициентов отрицателен, то данная поверхность – это однополосный гиперболоид с центром в начале координат и соответствующими полуосями: а = 1, b = 2, с = 3. Гиперболоид расположен вдоль оси Oz (квадрат этой координаты в уравнении с минусом). Сначала строим перпендикулярно оси Oz три сечения. Одно проходит через начало координат, два других – по обе стороны от него, например, в плоскостях z = 4 и z = – 4.
Этими сечениями являются эллипсы:

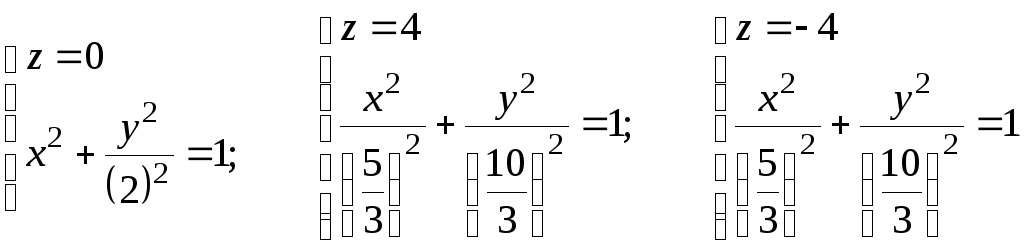 .
.
Вершины первого эллипса, называемого горловым, лежат в точках С2 (0, 2, 0), D2 (0, – 2, 0), A2 (1, 0, 0), B2 (– 1, 0, 0).
Второй эллипс,
расположенный в плоскости z
= 4, имеет вершины С1
(0,
![]() ,
4), D1
(0, –
,
4), D1
(0, –
![]() ,
4), A1
(
,
4), A1
(![]() ,
0, 4), B1
(–
,
0, 4), B1
(–![]() ,
0, 4).
,
0, 4).
Третий эллипс
расположен в плоскости z
= – 4, его вершинами служат точки С3
(0,
![]() ,
– 4), D3
(0, –
,
– 4), D3
(0, –
![]() ,
– 4), A3
(
,
– 4), A3
(![]() ,
0, – 4), B3
(–
,
0, – 4), B3
(–![]() ,
0, – 4).
,
0, – 4).
Теперь строим сечение однополосного гиперболоида координатной плоскостью уОz. В сечении получается гипербола

О на
расположена симметрично относительно
осей Оу
и Oz,
координаты ее вершин, лежащих на оси
Оу,
определяются решением системы
на
расположена симметрично относительно
осей Оу
и Oz,
координаты ее вершин, лежащих на оси
Оу,
определяются решением системы

Полученные точки (0; 2; 0) и (0; – 2; 0) являются уже известными нам вершинами С2 и D2 горлового эллипса.
Решая системы


получим соответственно точки С1 и D1, С3 и D3. Строим ветви гиперболы С1 С2 С3 и D1 D2 D3.
Аналогично, получаем гиперболы А1 А2 А3 и В1 В2 В3. в сечении однополосного гиперболоида плоскостью хОz.
Достраиваем поверхность и заключаем, что однополосный гиперболоид представляет собой бесконечную трубку, бесконечно расширяющуюся в обе сторон от горлового эллипса.
П р и м е р 15.
Построить тело, ограниченное поверхностями:
![]() ,
,
![]() .
.
Решение. Обе поверхности являются эллиптическими параболоидами. Первый параболоид имеет вершину в начале координат, а второй – в точке (0; 0; 15). Чтобы построить тело ограниченное этими поверхностями найдем плоскость их пересечения. Для этого решим систему уравнений:
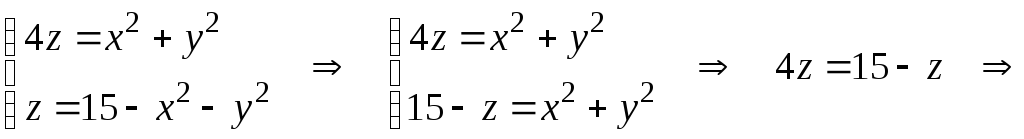
![]()
 .
.
Значит, поверхности
пересекаются на плоскости, параллельной
плоскости хОу,
на высоте z
= 3 и имеют сечение
![]() – окружность радиуса
– окружность радиуса
![]() .
.
Примеры для самостоятельного решения
1.
Составить уравнение плоскости, проходящей
через точку М
(2; – 1; – 4) и перпендикулярной вектору
![]() .
Ответ:
3 х
– 6 у
+ z
– 8 = 0.
.
Ответ:
3 х
– 6 у
+ z
– 8 = 0.
2. Определить отрезки, отсекаемые на осях координат плоскостями:
а) 2 х – 3 у + 4 z – 24 = 0 (Ответ: а = 12, b = – 8, с = 6);
б) 4 х + у – 3 z – 2 = 0 (Ответ: а = 1/2, b = 2, с = – 2/3)
3. Построить плоскости:
а) 2 х + 3 у – 4 z – 12 = 0; б) 2 х – 3 у – 6 = 0;
в) 4 х + 5 у = 0; г) 4 х + 9 = 0.
4. Написать уравнение плоскости, проходящей через точки А (– 2; 4; 1), В (0; 2; – 1), С (2; 0; – 1). Ответ: х + у – 2 = 0.
5. Найти угол между двумя плоскостями 11 х – 8 у – 7 z + 5 = 0 и 7 х + 2 у – 8 z – 3 = 0. Ответ: φ = 45º.
6. Составить канонические и параметрические уравнения прямых:
а)
 б)
б)

Ответ:
а)
![]() ;
;
 ;
б)
;
б)
![]() ;
;
 .
.
7. Даны вершины треугольника А (3; – 1; – 1), В (1; 2; – 7), С (– 5; 14; – 3). Найти угол В. Ответ: 74º42.
8. Найти расстояние
от точки С
(– 5; 4; 3) до прямой
![]() .
Ответ:
.
Ответ:
![]() .
.
9. Проверить, лежат
ли прямые
 и
и
 в одной плоскости.
в одной плоскости.
10. Найти величину
острого угла между прямой
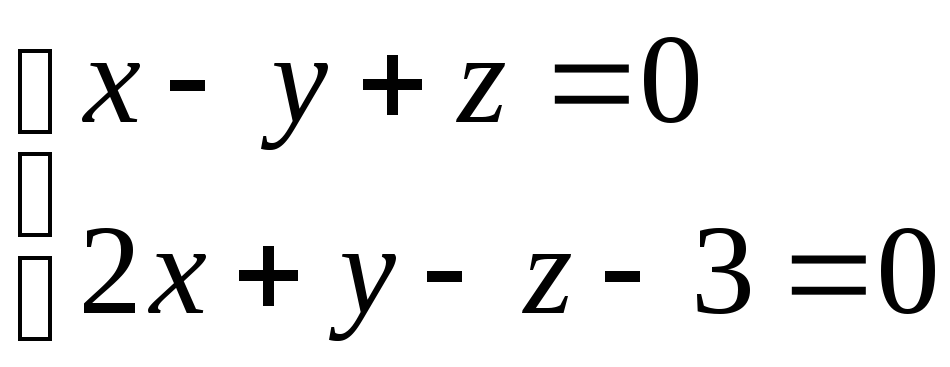 и плоскостью 2 х
+ у
+ 2 z
– 5 = 0. Ответ:
φ
= 45º.
и плоскостью 2 х
+ у
+ 2 z
– 5 = 0. Ответ:
φ
= 45º.
11. Определить следующие поверхности:
а) 3 х2 + 3 у2 + 3 z2 – 12 x + 15 y – 9 z + 33 = 0;
б) x2 + y2 + z2 – 2 x – 4 y + 8 z – 28 = 0;
в) 2 x2 – 6 y2 + 3 z2 – 12 x – 24 y – 24 z + 30 = 0;
г) – x2 + 2 y2 + 3 z2 – 4 x + 4 y – 24 z + 52 = 0;
д) x2 – 3 y2 + 8 x + 6 y + 10 = 0;
е) z2 – 8 x – 2 z – 7 = 0;
12. Определить и построить поверхности:
а) x2 + y2 – 4 z2 = – 1;
б) 3 x2 + y2 = 2 (z – 2);
в) y2 = 15 z;
г) x2 – 9 y2 = 4 z2;
д) x2 = 5 y – 1;
е) 2 x2 – 7 y2 + 11 z2 = 0;
ж)
![]() ;
;
