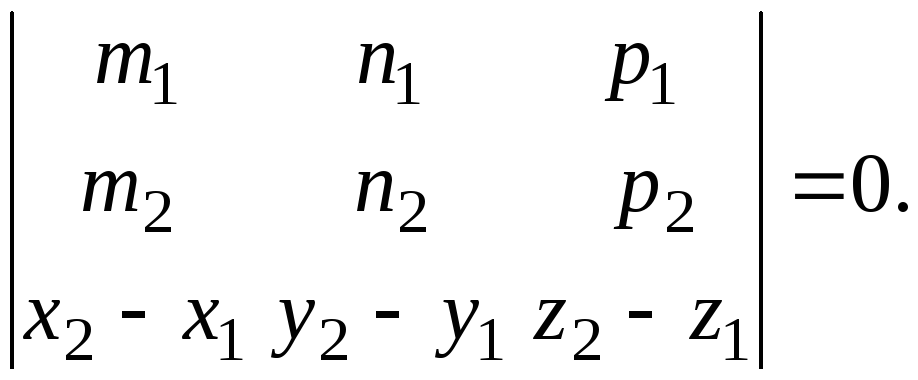- •Глава 5 Аналитическая геометрия в пространстве
- •§ 1. Плоскость
- •1. Угол между плоскостями.
- •2. Условие перпендикулярности двух плоскостей
- •3. Условие параллельности двух плоскостей
- •4. Условие совпадения плоскостей
- •§ 2. Прямая в пространстве
- •§ 3. Прямая и плоскость в пространстве
- •§4. Поверхности второго порядка
- •§ 4.1. Цилиндры второго порядка
- •§ 4.2. Эллипсоид, конус, гиперболоид
- •§ 4.3. Параболоиды.
- •«Прямая и плоскость в пространстве»
- •Решение практических задач по теме: «Плоскость»
- •Решение практических задач по теме: «Прямая в пространстве. Взаимное расположение прямой и плоскости»
- •Решение практических задач по теме: «Поверхности второго порядка»
- •Примеры для самостоятельного решения
§ 4.3. Параболоиды.
Характерный признак уравнения: содержит квадраты двух переменных с положительными множителями и первую степень третьей.
Особенности построения: осью симметрии поверхности является ось той переменной, которая входит в уравнение в первой степени.
Э ллиптический
параболоид.
ллиптический
параболоид.
а)
![]() а
> 0, b
> 0, сечением является эллипс, осью
симметрии – ось Oz
(смотри рисунок).
а
> 0, b
> 0, сечением является эллипс, осью
симметрии – ось Oz
(смотри рисунок).
б) Если a = b, то получаем параболоид вращения, а сечением является окружность (т. е. вращение параболы вокруг оси).
в)
![]() а
> 0, с
> 0, сечением является эллипс, осью
симметрии – ось Oу.
а
> 0, с
> 0, сечением является эллипс, осью
симметрии – ось Oу.
г )
)
![]() с
> 0, b
> 0, сечением является эллипс, осью
симметрии – ось Oz.
с
> 0, b
> 0, сечением является эллипс, осью
симметрии – ось Oz.
д)
![]() а
> 0, b
> 0, сечением является эллипс, ось Oz
(смотри рисунок).
а
> 0, b
> 0, сечением является эллипс, ось Oz
(смотри рисунок).
Гиперболический параболоид
Характерный признак уравнения: содержит квадраты двух переменных с множителями противоположных знаков и первую степень третьей.
Особенности построения: осью симметрии поверхности является ось той переменной, которая входит в уравнение в первой степени.
![]() а
> 0, b
> 0, сечением является гипербола, ось
симметрии Oz.
а
> 0, b
> 0, сечением является гипербола, ось
симметрии Oz.
а )
)
![]() а
>
0,
b
> 0, сечением является гипербола, ось
симметрии Oz
(смотри
рисунок).
а
>
0,
b
> 0, сечением является гипербола, ось
симметрии Oz
(смотри
рисунок).
б )
)
![]() а
> 0,
b
> 0, сечением является эллипс, ось Oz
(смотри
рисунок).
а
> 0,
b
> 0, сечением является эллипс, ось Oz
(смотри
рисунок).
в)
![]() с
> 0, a
> 0, сечением является гипербола, ось
симметрии Oу.
с
> 0, a
> 0, сечением является гипербола, ось
симметрии Oу.
г)
![]() с
> 0, b
> 0, сечением является гипербола, ось
симметрии Ox.
с
> 0, b
> 0, сечением является гипербола, ось
симметрии Ox.
Таблица понятий и формул по теме
«Прямая и плоскость в пространстве»
|
№ |
Понятие |
Содержание, формула |
|
П л о с к о с т ь |
||
|
1. |
Нормальный вектор
плоскости
|
Ненулевой вектор,
перпендикулярный данной плоскости
|
|
2. |
Общее уравнение плоскости. |
А х +
В у +
С z
+ D
= 0, где
|
|
3. |
Угол между двумя плоскостями (угол между нормалями). |
где
|
|
4. |
Условие перпендикулярности двух плоскостей (условие перпендикулярности векторов нормали). |
А1∙А2 + В1∙В2 + С1∙С2 = 0. |
|
5. |
Условие параллельности двух плоскостей (условие коллинеарности нормальных векторов). |
|
|
6. |
Условие совпадения плоскостей. |
|
|
7. |
Уравнение плоскости в отрезках. |
|
|
8. |
Уравнение
плоскости проходящей через данную
точку М0
(х0,
у0,
z0)
перпендикулярно вектору
|
А (х – х0) + В (у – у0) + С (z – z0) = 0. |
|
9. |
Уравнение плоскости, проходящей через три заданные точки М1 (х1, у1, z1), М2 (х2, у2, z2) и М3 (х3, у3, z3). |
|
|
10. |
Расстояние d от точки М0 (х0, у0, z0) до плоскости А∙х + В∙у + С∙z + D = 0. |
|
|
П р я м а я |
||
|
11. |
Направляющий
вектор прямой
|
Ненулевой вектор,
параллельный данной прямой или лежащий
на ней
|
|
12. |
Общее уравнение прямой (пересечение двух плоскостей). |
|
|
13. |
Канонические уравнения прямой. |
|
|
14. |
Угол между двумя прямыми (угол между направляющими векторами). |
|
|
15. |
Условие параллельности двух прямых (коллинеарность направляющих векторов). |
|
|
16. |
Условие перпендикулярности двух прямых (перпендикулярность направляющих векторов). |
|
|
17. |
Уравнение прямой, проходящей через две точки М1 (х1, у1, z1), М2 (х2, у2, z2). |
|
|
18. |
Параметрические уравнения прямой. |
|
|
П р я м а я и п л о с к о с т ь |
||
|
19. |
Угол между прямой
|
|
|
20. |
Условие параллельности прямой и плоскости (перпендикулярность направляющего вектора прямой и нормального вектора плоскости). |
|
|
21. |
Условие перпендикулюрности прямой и плоскости (коллинеарность направляющего вектора прямой и нормального вектора плоскости). |
|
|
22. |
Условие принадлежности прямой плоскости. |
Одновременное
выполнение равенств
|
|
23. |
Условие
принадлежности двух прямых
|
|



 .
.