
- •Глава 5 Аналитическая геометрия в пространстве
- •§ 1. Плоскость
- •1. Угол между плоскостями.
- •2. Условие перпендикулярности двух плоскостей
- •3. Условие параллельности двух плоскостей
- •4. Условие совпадения плоскостей
- •§ 2. Прямая в пространстве
- •§ 3. Прямая и плоскость в пространстве
- •§4. Поверхности второго порядка
- •§ 4.1. Цилиндры второго порядка
- •§ 4.2. Эллипсоид, конус, гиперболоид
- •§ 4.3. Параболоиды.
- •«Прямая и плоскость в пространстве»
- •Решение практических задач по теме: «Плоскость»
- •Решение практических задач по теме: «Прямая в пространстве. Взаимное расположение прямой и плоскости»
- •Решение практических задач по теме: «Поверхности второго порядка»
- •Примеры для самостоятельного решения
§ 3. Прямая и плоскость в пространстве
1 .
Угол между
прямой и плоскостью.
Пусть даны прямая
.
Угол между
прямой и плоскостью.
Пусть даны прямая
![]()
и плоскость
П: А х + В у + С z + D = 0.
Углом φ между прямой и плоскостью называют наименьший из углов, образованных прямой с ее проекцией на плоскость. Из рисунка видно, что
![]() откуда
откуда
![]() .
.
Учитывая, что
 и
и
![]()
находим
![]() .
(15)
.
(15)
2 .
Условия
параллельности и перпендикулярности
прямой и плоскости.
.
Условия
параллельности и перпендикулярности
прямой и плоскости.
L
П
П
![]()
L
||
П
![]()
![]()
![]()
3. Точка пересечения прямой с плоскостью. Пусть требуется найти точку пересечения прямой L:
![]()
с плоскостью П: А∙х + В∙у + С∙z + D = 0.
Проще всего это сделать с помощью параметрических уравнений прямой:
 (16)
(16)
Каждому значению параметра t соответствует точка прямой. Нужно выбрать такое значение t, при котором точка прямой L будет лежать на плоскости П. Подставляя х, у, z из соотношений (7) в уравнение плоскости П, получим уравнение, из которого найдем значение параметра t. Затем найденное значение параметра t подставляем в уравнения (7). Полученные таким образом х, у, z и будут координатами точки пересечения прямой L и плоскости П.
4. Условие принадлежности прямой плоскости П. Пусть прямая L и плоскость П заданы уравнениями:
![]() ,
,
![]() .
.
Для того чтобы прямая L принадлежала плоскости П, необходимо и достаточно, чтобы одновременно выполнялись два условия:
– перпендикулярность
векторов
![]() и
и
![]() ;
;
– точка М0 прямой L лежала на плоскости, т. е. ее координаты удовлетворяли уравнению плоскости, а именно
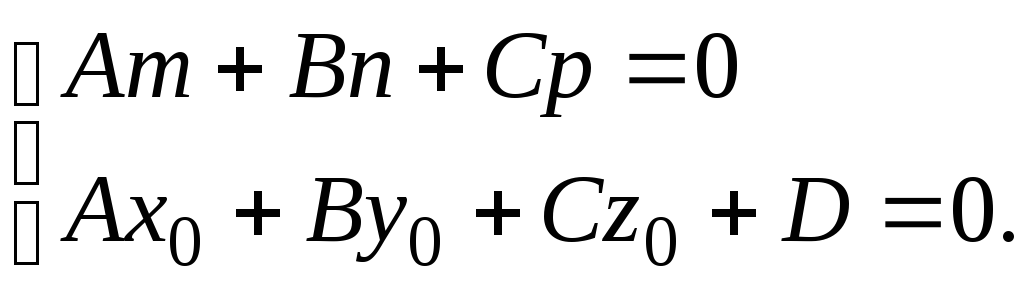 (17)
(17)
5. Условие принадлежности двух прямых одной плоскости. Пусть прямые L1 и L2 заданы уравнениями
![]()
Данные прямые
лежат в одной плоскости в том и только
в том случае, если их направляющие
векторы
![]() и
и
![]() и
и
![]() компланарны, т. е.
компланарны, т. е.
![]()
 или
или
 (18)
(18)
§4. Поверхности второго порядка
К поверхностям второго порядка относятся цилиндры, эллипсоиды, конусы, параболоиды и гиперболоиды. В декартовых координатах эти поверхности описываются уравнением: F (x, y, z), левая часть которого есть целый многочлен второй степени относительно x, y, z.
Поверхности второго порядка можно разбить на три группы. В каждой из них канонические уравнения поверхностей имеют общий признак, которому соответствуют некоторые особенности в расположении их относительно системы координат.
Рассмотрим канонические уравнения и изображение поверхностей каждой группы с указанием характерного признака в уравнении и особенности в расположении относительно системы координат.
§ 4.1. Цилиндры второго порядка
Определение 6. Цилиндрической поверхностью называется поверхность, описываемая прямой (образующая) движущейся вдоль некоторой линии (направляющая) и остающейся параллельной исходному направлению.
О пределение
7. Цилиндром
второго порядка
называется цилиндрическая поверхность,
направляющей которой является окружность,
эллипс, гипербола или парабола.
пределение
7. Цилиндром
второго порядка
называется цилиндрическая поверхность,
направляющей которой является окружность,
эллипс, гипербола или парабола.
Характерным признаком уравнений цилиндров второго порядка является отсутствие в этом уравнении одной из текущих координат.
Особенности построения: образующие параллельны той оси, координата которой отсутствует в уравнении. Уравнение направляющей совпадает с уравнением поверхности.
Таким образом, цилиндрические поверхности определяются одним из следующих уравнений:
F
(x,
y)
= 0: образующая параллельна оси Оz,
направляющая:

F
(y,
z)
= 0: образующая параллельна оси Оx,
направляющая:
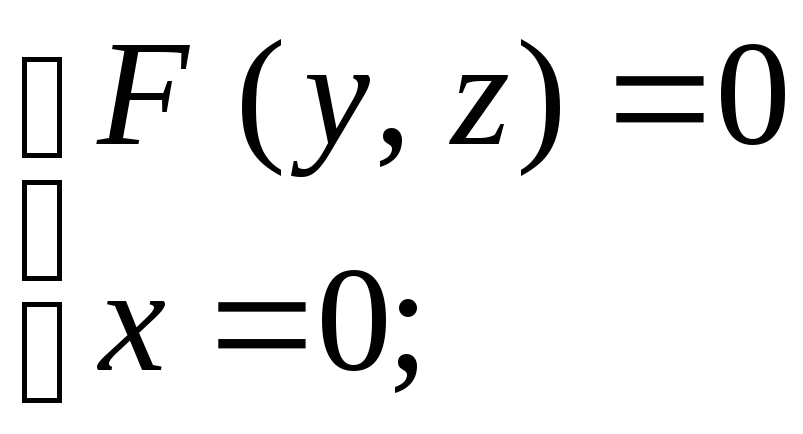
F
(x,
z)
= 0: образующая параллельна оси Оy,
направляющая:

Составим таблицу цилиндров второго порядка.
|
Эллиптический цилиндр: направляющей является эллипс. |
||
|
|
Направляющая –
Образующая || Oz. |
|
|
|
Направляющая –
Образующая || Oх. |
|
|
|
Направляющая –
Образующая || Oу. |
|
|
К |
||
|
|
а = R; b = R; c = R.
|
|
|
Г |
||
|
|
а)
Направляющая –
Образующая || Oz, ось Ох – мнимая. |
|
|
|
б)
Направляющая –
Образующая || Oz, ось Оу – мнимая. |
|
|
в)
Образующая || Oу, ось Ох – мнимая.
г)
Образующая || Oу, ось Оz – мнимая.
д)
Образующая || Ox, ось Оy – мнимая.
е)
Образующая || Ox, ось Оz – мнимая. |
||
|
П |
||
|
|
а) y2
= 2 p
x,
образующая || оси Оz,
направляющая:
|
|
|
|
б)
х2
= 2 p
у, образующая
|| оси Оz,
направляющая:
|
|
|
в) y2
= 2 p
z,
образующая || оси Оx,
направляющая:
|
||
|
г) z2
= 2 p
y,
образующая || оси Оx,
направляющая:
|
||
|
д) x2
= 2 p
z,
образующая || оси Оy,
направляющая:
|
||
|
е) z2
= 2 p
x,
образующая || оси Оy,
направляющая:
|
||



 .
.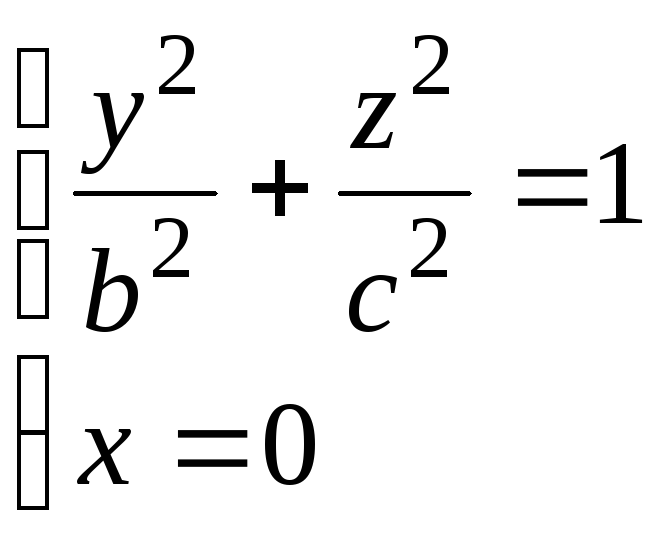 .
.
 .
. руговой
цилиндр:
направляющей является окружность.
руговой
цилиндр:
направляющей является окружность. иперболический
цилиндр:
направляющей является гипербола.
иперболический
цилиндр:
направляющей является гипербола. .
.
 .
.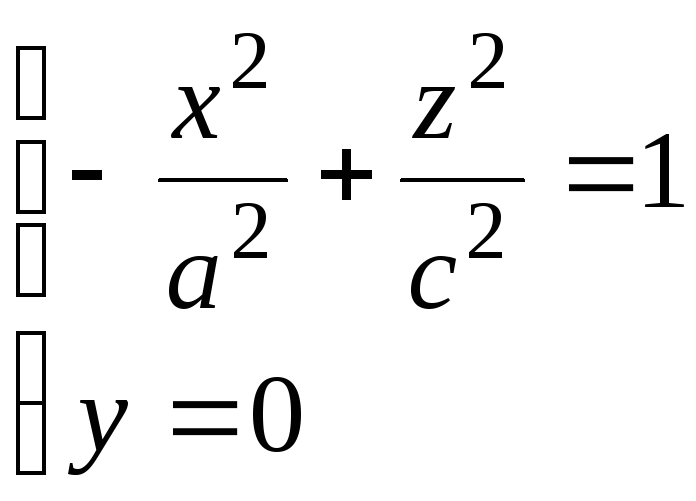 .
. .
. .
. .
. араболический
цилиндр:
направляющей является парабола.
араболический
цилиндр:
направляющей является парабола. .
.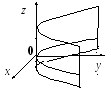
 .
.


