§7. Векторное произведение векторов
О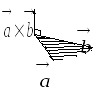
пределение
21. Векторным
произведением
векторов
и
называется вектор
,
который определяется следующим образом:
1.;
2. вектор
и
,
т.е. вектор векторного произведения
перпендикулярен
каждому
из
перемножаемых
векторов, т. е.
3. векторы
образуют правую тройку.
Свойства векторного произведения
1. Модуль векторного
произведения
равен площади параллелограмма,
построенного на
и
как на сторонах
.
(10)
2.
.
3.
.
4.
.
5.
Векторное
произведение в декартовых координатах,
где
,
имеет вид
.
(11)
§8. Смешанное произведение трех векторов
Определение 22.
Смешанным
произведением
векторов
называется число, получаемое в результате
скалярного умножения
и обозначаемое
.
.
Свойства смешанного произведения
1. Абсолютная
величина смешанного произведения
равна объему параллелепипеда построенного
на векторах
с общим началом как на ребрах
.
(12)
2.
> 0, когда базис
правый.
< 0, когда базис
левый.
3. Смешанное
произведение не изменяется при циклической
перестановке сомножителей:
;
оно меняет знак при перестановке двух
сомножителей:
.
4.
.
5.
.
6.
– компланарны.
Смешанное
произведение в декартовых координатах.
Пусть
,
,
тогда
.
(13)
Сводная таблица основных понятий и формул по теме «Векторы»
|
№ |
Понятие |
Содержание, формула |
|
1. |
Скалярная величина |
Величина, которая может быть задана числом в выбранной системе единиц. |
|
2. |
Вектор |
Величина, которая задается числовым значением и направлением. |
|
3. |
Коллинеарные векторы |
Векторы, лежащие на параллельных прямых или на одной прямой. |
|
4. |
Координаты
вектора
|
Коэффициенты X,
Y,
Z
в разложении вектора
|
|
5. |
Условие
коллинеарности векторов, заданных
координатами
|
Пропорциональность их соответствующих координат:
|
|
6. |
Направляющие
косинусы вектора
|
Косинусы углов, образуемых вектором с положительными направлениями осей Ох, Оу, Oz:
|
|
7. |
Скалярное
произведение вектора
|
Число, равное произведению их модулей на косинус угла между ними:
|
|
8. |
Скалярное
произведение векторов
|
|
|
9. |
Вычисление угла
между векторами
|
|
|
10. |
Условие перпендикулярности (ортогональности) двух векторов. |
|
|
11. |
Модуль векторного
произведения вектора
|
|
|
12. |
Векторное
произведение векторов
|
|
|
13. |
Площадь
параллелограмма, построенного на
|
|
|
14. |
Смешанное
произведение векторов
|
Число, получаемое
в результате скалярного умножения
|
|
15. |
Объем параллелепипеда
построенного на векторах
|
|
|
16. |
Смешанное
произведение векторов
|
|
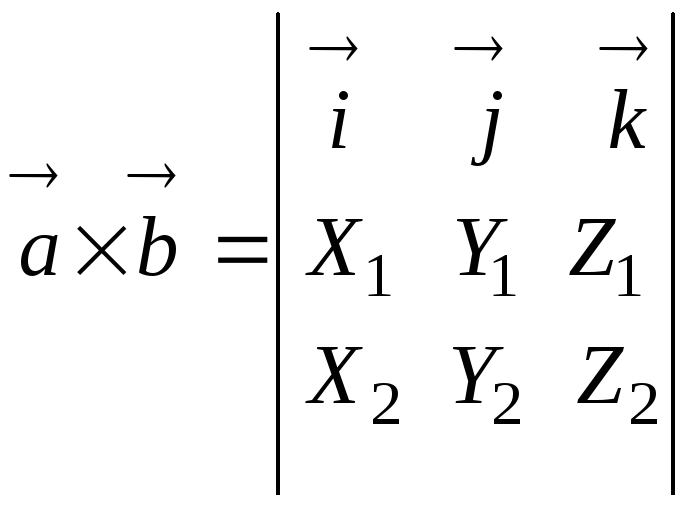
в базисе
.
по базису
:
.
и
.
.
,
.
на вектор
.
и
,
заданных в координатной форме.
и
.
.
на вектор
.
.
и
,
заданных в координатной форме.
и
как на сторонах.
.
.
и обозначаемое
.
.
с общим началом как на ребрах.
,
,
и
заданных в координатной форме.