Практическое занятие №8 элементы математической статистики

Цель: овладение навыками количественного анализа статистических совокупностей.

Контрольные вопросы

1. Какие основные задачи решает математическая статистика?

2. Генеральная и выборочная совокупность? Дайте определение объема выборки.

3. Какие выборки называются репрезентативными? Ошибки репрезентативности.

4. Основные способы образования выборки.

5. Понятия частоты, относительной частоты.

6. Понятие статистического ряда. Запишите формулу Стэрджеса.

7. Сформулируйте понятия размаха выборки, медианы и моды.

8. Полигон частот, гистограмма.

9. Понятие точечной оценки выборочной совокупности. Смещенная и несмещенная точечная оценка.

10. Выборочная средняя, выборочная дисперсия, исправленная дисперсия, выборочное среднеквадратическое отклонение, выборочный коэффициент вариации.

11. Объясните, что такое выборочное распределение средних.

12. Что такое доверительная вероятность и уровень значимости? Как они связаны между собой?

13. Доверительный интервал.

14. Запишите, по какой формуле вычисляется предельная ошибка в случае малой выборки и в случае большой выборки.

15. В чем заключается закон больших чисел?

Примеры решения типовых задач

Пример 8.1.

Задано распределение частот выборки объема = 50:

	10	20	30	40
	13	7	18	12

Записать распределение относительных частот.

Решение:

, , ,

Сделаем проверку:

	10	20	30	40
	0,26	0,14	0,36	0,24

Пример 8.2.

В течение первого полугодия в городе Октябрьский были привлечены к ответственности за взятки 25 человек: 5, 3, 7, 2, 4, 4. Найдите генеральную среднюю, дисперсию, среднеквадратическое отклонение и коэффициент вариации для случайной величины – количество привлеченных к ответственности за взятки.

Решение:

Заполним следующую таблицу:

Месяц	Количество привлеченных , человек
Январь	5	25
Февраль	3	9
Март	7	49
Апрель	2	4
Май	4	16
Июнь	4	16
Сумма	25	119
Среднее	4,17	19,83

Таким образом, генеральная средняя равна:

Дисперсия: .

Среднее квадратическое отклонение:

Коэффициент вариации: .

Пример 8.3.

Найти выборочную среднюю, выборочную дисперсию, исправленную дисперсию, среднеквадратическое отклонение и коэффициент вариации по данному распределению выборки:

xi	2	4	5	7
ni	5	10	4	6

Решение:

Объем выборки:

Выборочная средняя:

Выборочная дисперсия:

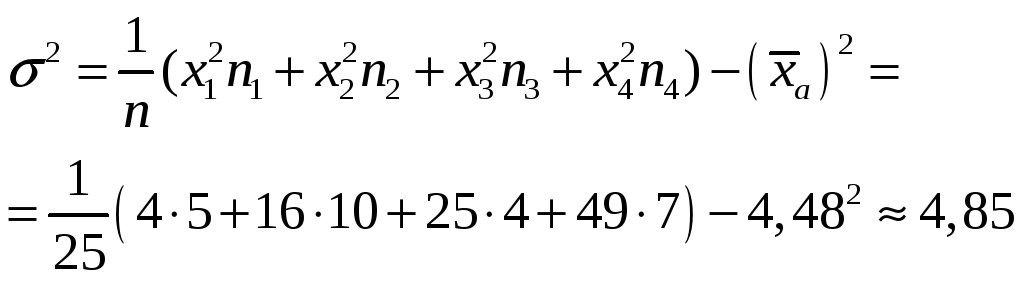
Исправленная дисперсия:

.

Среднеквадратическое отклонение:

Коэффициент вариации:

.

Пример 8.4.

Производительность труда рабочих промышленного предприятия характеризуется следующими данными:

№	Выработка изделий рабочим за смену, штук	Численность рабочих, человек
1	20-30	5
2	30-40	25
3	40-50	50
4	50-60	12
5	60-70	8

Найдите среднюю производительность труда, используя для расчета, формулы средней арифметической, медианы и моды.

Решение:

При расчете в качестве значений возьмем середины интервалов: 25, 35, 45, 55, 65.

Найдем медианный интервал: . Признак, соответствующий данному номеру находится в третьем интервале. Он и будет являться медианным. Рассчитаем значение медианы:

.

Модальным интервал также будет третий, поскольку он соответствует наибольшей частоте. Рассчитаем значение моду:

.

Пример 8.5.

При случайном повторном отборе было установлено, что средний вес товара в выборочной совокупности, состоящей из 90 изделий, оказался равным 8,2 кг при среднем квадратическом отклонении 0,5 кг. С вероятностью, равной 0,954, определите, в каких пределах заключен средний вес товара в генеральной совокупности.

Решение:

Найдём . Из отношения 4 получим . По таблице находим . Предельная ошибка равна:

Округление дает значение предельной ошибки .

Доверительный интервал: , , .

Ответ средний вес товара с надежностью 0,954 заключен в диапазоне .

Задачи для самостоятельного решения:

8.1. В одном из районов г. Москвы в течение второго полугодия было совершено 30 преступлений с применением огнестрельного оружия: 7, 3, 6, 5, 6, 3. Найдите среднюю арифметическую, дисперсию, среднеквадратическое отклонение и коэффициент вариации для данной генеральной совокупности.

8.2. При выборочном исследовании некоторой генеральной совокупности по признаку , были получены следующие данные: 5, 6, 6, 7, 9, 10, 8, 7, 7, 5. Найти выборочную среднюю, выборочную дисперсию, исправленную дисперсию, среднеквадратическое отклонение и коэффициент вариации исследуемого признака.

8.3. Найти выборочную среднюю, выборочную дисперсию, исправленную дисперсию, среднеквадратическое отклонение и коэффициент вариации по данному распределению выборки:

xi	5	13	17	19
ni	10	6	4	5

8.4. Найти выборочную среднюю, выборочную дисперсию, исправленную дисперсию, среднеквадратическое отклонение и коэффициент вариации по данному распределению выборки:

xi	8	10	11	12
ni	5	6	3	2

8.5. Имеются данные о заработной плате одного из предприятий города.

№ интервала	Заработная плата, тыс. руб.	Численность работников, человек
1	10-20	7
2	20-30	23
3	30-40	40
4	40-50	15
5	50-60	5

1) Постройте гистограмму данного распределения. 2) Найдите среднюю заработную плату, используя для расчета, формулы средней арифметической, медианы и моды.

8.6. Имеются следующие данные о распределении посевной площади фермерского хозяйства по урожайности пшеницы:

№ интервала	Урожайность пшеницы , ц/га	Посевная площадь , га
1	16-18	50
2	18-20	78
3	20-22	62
4	22-24	40

Найдите среднюю урожайность пшеницы, дисперсию и среднее квадратическое отклонение.

8.7. При случайном повторном отборе было установлено, что средний вес товара в выборочной совокупности, состоящей из 121 изделия, оказался равным 8 кг при дисперсии 0,36 кг. С вероятностью, равной 0,95, определите, в каких пределах заключен средний вес товара в генеральной совокупности.

8.8. Генеральная совокупность изучается выборочным повторным методом по некоторому признаку . Какой объем выборки будет гарантировать, что предельная ошибка не превысит значения 3,5 с вероятностью 0,95?

8.9. Количественный признак генеральной совокупности распределен нормально. По выборке объема найдены выборочная средняя , исправленное среднее квадратическое отклонение . Определите, доверительный интервал генеральной средней с надежностью 0,954 (выборка повторная).

8.10. В результате выборочного повторного обследования генеральной совокупности по признаку (предполагается, что он распределен нормально) были получены следующие данные 4,5; 5,3; 8,6; 6,7; 6,6; 7,0; 7,1; 7,2; 5,8. Определите доверительный интервал генеральной средней на уровне значимости 0,05.

Домашнее задание:

1) Лекция №11 (пп. 4, 5)

2) Одним и тем же прибором со средним квадратическим отклонением случайных ошибок измерений м произведено девять равноточных измерений расстояния от орудия до цели. Найти доверительный интервал для оценки истинного расстояния а до цели на уровне значимости 0,05, зная среднее арифметическое результатов измерений м. Предполагается, что результаты измерений распределены нормально.