Практическое занятие №3 предел функции
Цель: формирование навыков решения
задач по нахождению пределов функции
с неопределенностью вида:
и
.
Контрольные вопросы
1. Сформулируйте понятие числовой последовательности.
2. Какая числовая последовательность называется ограниченной?
3. Какая точка называется предельной для данной числовой последовательности.
4. Сформулируйте теорему Больцано-Вейерштрассе.
5. Сформулируйте понятие предела числовой последовательности.
6. В чем заключается геометрический смысл предела числовой последовательности?
7. Сформулируйте понятие функции. Способы задания функции.
8. Сформулируйте понятие предела функции.
9. Запишите основные свойства пределов.
10. Запишите первый и второй замечательные пределы.
Примеры решения типовых задач
Пример 3.1.
Вычислить предел:
Решение:
Пример 3.2.
Вычислить предел:
Решение:
Если вместо
подставить 2, то получится неопределенность
вида
.
Чтобы избавится от нее, преобразуем
числитель и знаменатель:
Числитель:
Знаменатель:
,
Таким образом:
Пример 3.3.
Вычислить предел:
Решение:
Если вместо
подставить
,
то получится неопределенность вида
.
Чтобы избавится от нее разделим числитель
и знаменатель на
:
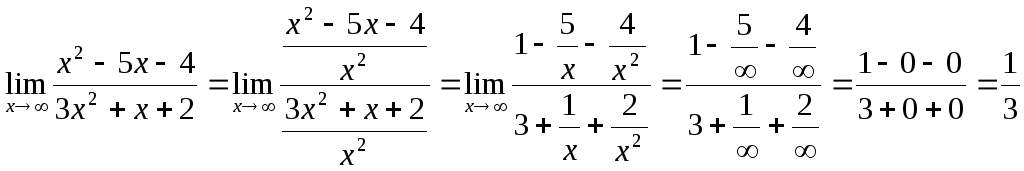
Пример 3.4.
Вычислить предел:
Решение:
Если вместо
подставить 0, то получится неопределенность
вида
Преобразуем данный предел:
Здесь использовали замену
и первый замечательный предел.
Пример 3.5.
Вычислить предел:
Решение:
Здесь выполнили замену
и второй замечательный предел.
Задачи для самостоятельного решения:
3.1.
3.2.
;
3.3.
;
3.4.
;
3.5.
;
3.6.
Ответы: 3.1. 7; 3.2. -1; 3.3. 2; 3.4.
2; 3.5.
;
3.6.
.
Практическое занятие №4 дифференциальное исчисление функции одной переменной
Цель: формирование навыков решения задач по нахождению производной от функции. Решения задач по исследованию функции на интервалы возрастания и убывания, а также точки максимумов и минимумов.
Контрольные вопросы
1. Сформулируйте понятие непрерывной функции в данной точке.
2. Сформулируйте понятие точки разрыва функции.
3. В чем принципиальное различие между точками разрыва первого и второго рода?
4. Сформулируйте понятие производной функции одной переменной.
5. Какая функция называется дифференцируемой в данной точке?
6. В чем состоит геометрический смысл производной?
7. Запишите правило дифференцирования суммы функций.
8. Запишите правило дифференцирования частного функций.
9. Запишите правило нахождения производной от произведения функций.
10. Сформулируйте правило дифференцирования сложных функций.
11. Сформулируйте понятие дифференциала функции одной переменной.
12. Сформулируйте понятие точек максимумов и минимумов функции.
13. Запишите необходимый и достаточный признаки существования точек экстремумов функции.
Пример 4.1.
Найти производную
функции:
Решение:
Пример 4.2.
Найти производную
функции:
.
Решение:
Воспользуемся
правилом дифференцирования произведения
функций:
Пример 4.3.
Найти производную
функции:
Решение:
Воспользуемся
правилом дифференцирования частного
Пример 4.4.
Найти производную
сложной функции:
Решение:
Пример 4.5.
Исследовать на
максимум и минимум функцию:
Решение:
Находим критические точки. Продифференцируем данную функцию:
Находим действительные корни производной:
;
.
Производная всюду непрерывна, значит, других критических точек нет.
Исследуем первую
критическую точку
.
Так как
,
то:
При
имеем
;
При
имеем
.
Значит, при переходе
(слева направо) через значение
производная меняет знак с плюса на
минус. Следовательно, при
функция имеет максимум.
Исследуем вторую
критическую точку
:
При
имеем
;
При
имеем
.
Значит, при переходе
(слева направо) через значение
производная меняет знак с минуса на
плюс. Следовательно, при
функция имеет минимум.
.
Пример 4.6.
Найти прямоугольный треугольник наибольшей площади, имеющий гипотенузу, равную 10 см.
Решение:
Площадь прямоугольного
треугольника
можно найти по формуле:
,
где
и
длины катетов. Согласно теореме Пифагора:
,
где
- длина гипотенузы.
Таким образом, подставив данное выражение в формулу для нахождения площади, получим функцию одной переменной:
.
Нам необходимо
найти прямоугольный треугольник
наибольшей площади, т.е. по сути, нам
необходимо исследовать на экстремумы
функцию
и найти при каком значении
она максимальна.
Находим производную
от функции
:
Находим критические
точки:
,
,
Используя достаточный признак
существования экстремума функции, можно
определить, что точкой максимума будет
.
Тогда длина второго катета будет равна:
.
Таким образом, максимальная площадь
будет равна:
см2.
Задачи для самостоятельного решения:
4.1. Найти производные функций:
а)
;
б)
;
в)
; г)
.
4.2. Найти производную сложной функции:
а)
;
б)
;
в)
;
г)
.
4.3. Найти экстремумы функции:
а)
;
б)
.
4.4.
Найти наибольшее и наименьшее значения
функции
на отрезке
.
4.5. В тюрьме города Ленинск собрались строить железную камеру для содержания особо опасных преступников. Какое наименьшее количество железа нужно для этой цели, если по санитарным нормам высота камеры должна быть не менее 2,5 м, а ее площадь — не менее 6 м2?
Ответы: 4.1.а
;
4.1б.
;
4.1в.
;
4.1г.
;
4.2а.
;
4.2б.
;
4.2в.
;
4.2г.
.
4.3а.
при
;
4.3б.
при
,
при
;
4.4. Наибольшее
значение
при
,
наименьшее значение
при
;
4.5.
36,5
м2
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5
СЛУЧАЙНЫЕ СОБЫТИЯ
СЛОЖЕНИЕ И УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ
Цели: 1) Формирование основных представлений теории вероятностей: случайные события, совместные и несовместные события, вероятность и т.д. 2) Формирование навыков расчета вероятностей на основании классического определения вероятности. 3) Формирование навыков решение задач с использованием теорем сложения и умножения вероятностей.
Контрольные вопросы
1. Сформулируйте понятие случайного события.
2. Совместные и несовместные события.
3. Достоверные и невозможные события.
4. Какие события называются единственновозможными?
5. Какие события образуют полную группу? Противоположные события?
6. Классическое определение вероятности. Диапазон изменения вероятности случайного события.
7. Правило умножения в комбинаторике. Понятие факториала.
8. Перестановка, сочетание, размещение, размещение с повторениями.
9. Сумма нескольких событий.
10. Теорема сложения двух совместных событий.
11. Теорема сложения двух несовместных событий.
12. Произведение двух событий.
13. Какие события называются независимыми в совокупности?
14. Вероятность совместного появления двух зависимых событий. Условная вероятность.
15. Вероятность совместного появления двух независимых событий.
Пример 5.1.
В ящике 7 белых и 9 черных шаров. Наугад вынимают 1 шар. Найти вероятность того, что будет вынут шар черного цвета
Решение:
Пусть A – событие, состоящее в том, что вынутый черный шар.
=7+9=15
– число всех равновозможных исходов
опыта.
=9
– число исходов благоприятствующих
событию
.
Воспользуемся
формулой классической вероятности:
;
.
Пример 5.2.
В колоде 36 карт. Найти вероятность того, что вытащенная наугад карта из колоды оказалась королям (ответ:1/9).
Решение:
Пусть A – событие, состоящее в том, что из колоды вынули короля.
Воспользуемся
формулой классической вероятности:
.
В колоде 36 карт,
значит
= 36 – число всех равновозможных исходов
опыта.
Поскольку в колоде
всего четыре короля, то
= 4 – число исходов благоприятствующих
появлению события
.
.
Пример 5.3.
На карточке спортлото 36 клеток. Играющий должен отметить 4. Каково число всех возможных вариантов?
Решение:
Из условия задачи следует, что необходимо найти число сочетаний 4 из 36. Воспользуемся формулой:
Пример 5.4.
В ящике 15 деталей, среди которых 10 нестандартных. Сборщик наудачу извлекает 4 детали. Найти вероятность того, что среди извлеченных деталей две будут нестандартные.
Решение:
Пусть событие
– среди извлеченных 4 деталей 2
нестандартные.
– общее число
четверок, которые можно сформировать
из 15 деталей
– число четверок,
благоприятствующих событию А.
По формуле
Пример 5.5.
Студент сдает экзамен по теории вероятностей. Вероятность получить на экзамене «2» равна 0,1; «3» – 0,6; «4» – 0,2; «5» – 0,1. Какова вероятность того, что студент получит на экзамене положительную оценку?
Решение:
Пусть событие А – студент получит на экзамене положительную оценку.
,
т.к. событие А
и событие «2» – получить двойку на
экзамене являются противоположными.
.
Пример 5.6.
Вероятность того, что первый стрелок поразит мишень равна 0,8, второй – 0,5. Найти вероятность того, мишень будет поражена только один раз.
Решение:
Пусть событие А
– попадет первый стрелок.
.
Событие
– мишень поразит второй стрелок.
.
Интересующее нас событие
– будет ровно одно попадание по мишени,
если стрелки сделают только по одному
выстрелу.
Вероятность того,
что первый стрелок не попадет:
.
Второй стрелок не попадет с вероятностью
.
Вероятность события
равна:
.
Пример 5.7.
Две пушки стреляют
по мишени. Вероятность поражения мишени
первой пушкой равна
=0,75,
второй
=0,6.
Какова вероятность того, что мишень
будет поражена, если пушки сделают по
одному залпу? События
и
независимы.
Решение:
Интересующие нас
событие
– будет поражена мишень.
Мишень будет поражена либо когда будет одно попадание, либо два. Таким образом, необходимо найти вероятность хотя бы одного попадания по мишени. Воспользуемся теоремой сложения совместных событий:
Поскольку события
и
независимы, данную формулу перепишем
в следующем виде:
.
Пример 5.8.
В урне находятся 7 белых и 3 черных шара. Подряд извлекают 2 шара. Какова вероятность того, что оба они черные.
Решение:
Пусть событие А – первый шар черный, событие В – второй шар черный.
Данная задаче решается с использованием теоремы о вероятности совместного появления двух зависимых событий.
.
Задачи для самостоятельного решения:
5.1. В урне находятся 16 белых и 8 черных шаров. Какова вероятность того, что наудачу вынутый шар будет белым?
5.2. Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 5.
5.3. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором 3 вопроса.
5.4. Преступник знает, что шифр сейфа составлен из цифр 1, 3, 5 и 8, но не знает, в каком порядке их набирать. Какова вероятность того, что преступник откроет сейф с первой попытки?
5.5. В урне 6 белых и 4 черных шара. Из этой урны наудачу извлекли 5 шаров. Какова вероятность того, что 2 из них белые, а 3 черные?
5.6.
Какова вероятность того, что в компании
из
человек хотя бы у двоих совпадут дни
рождения? (Для простоты предполагается,
что 29 февраля не является днем рождения).
5.7. Три стрелка независимо друг от друга стреляют по мишени. Вероятность попадания в цель для первого стрелка равна 0,7, для второго – 0,85, для третьего – 0,6. Определить вероятность того, что один стрелок попадет в цель.
5.8.
Студент сдает два экзамена: экономику
и математику. Вероятность сдачи экономики
равна
,
а математики –
.
Найти вероятность того, что студент:
а) сдаст два экзамена,
б) сдаст один экзамен,
в) сдаст хотя бы один экзамен;
г) не сдаст ни одного экзамена;
д) сдаст сессию?
5.9. Из колоды в 36 карты наугад одна за другой вынимаются две карты. Найти вероятность того, что вынули валет и короля.
5.10. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.
5.11. Из четырех человек A, B, C, D один (A) получил информацию, которую в виде сигнала «да» или «нет» сообщает второму (B), второй – третьему (С), третий – четвертому (D), а последний (D) объявляет результат полученной информации таким же образом, как и все другие. Известно, что каждый из них говорит правду только в одном случае из трех. Какова вероятность того, что первый из лгунов сказал правду, если четвертый сказал правду?
Домашнее задание: 1) Владелец одной карточки лотереи «Спортлото» (6 из 49) зачеркивает 6 номеров. Какова вероятность того, что им будет угадано все 6 номеров в очередном тираже. 2) Лекция №7 (п. 2,3).