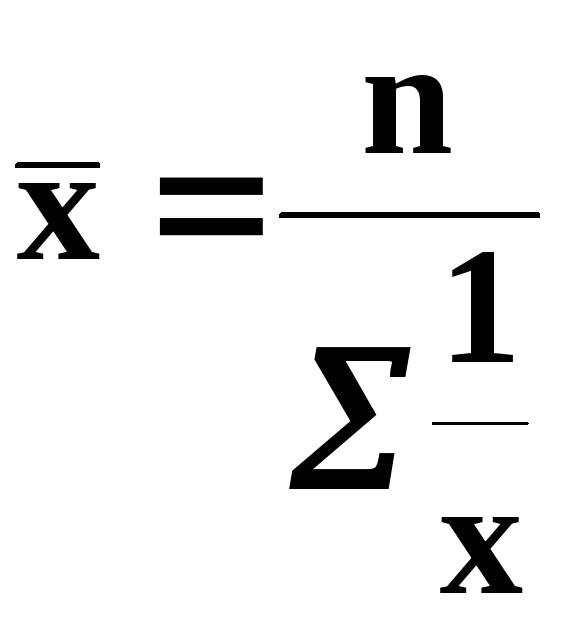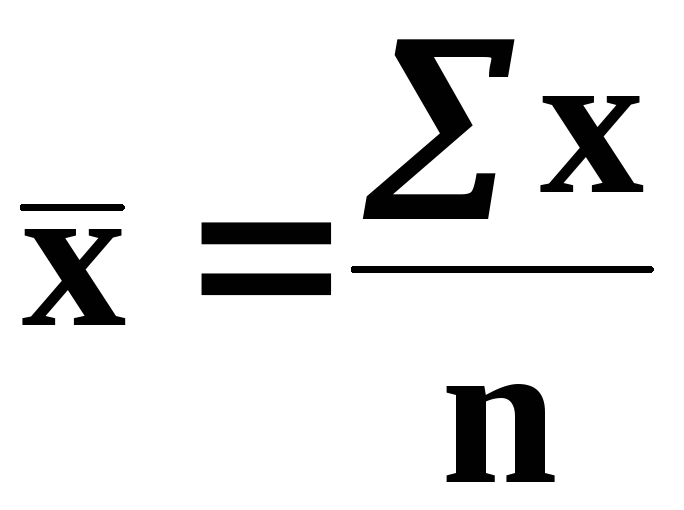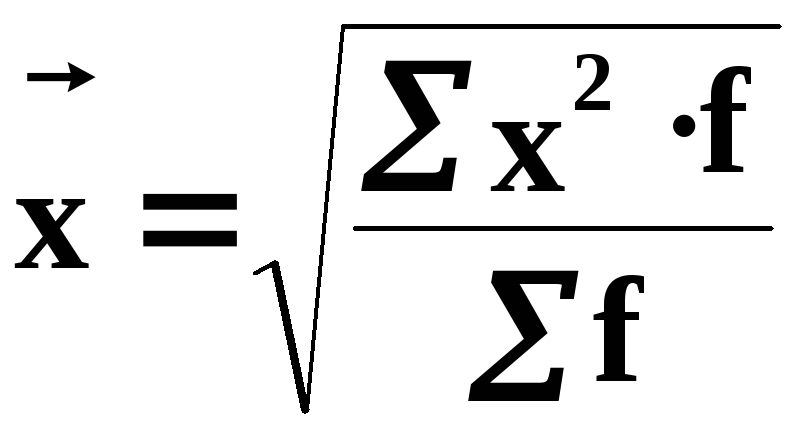Средние величины

Средней величиной называется обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.

Объективность и типичность статистической средней обеспечивается лишь при определенных условиях. Первое условие -средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок. Второе условие - для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине признака, вызванные случайными причинами, погашаются и проявляется общее свойство (типичный размер признака) для всей совокупности.

Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.

При использовании средних в практической работе и научных исследованиях необходимо иметь в виду, что за средним показателем скрываются особенности различных частей изучаемой совокупности, поэтому общие средние для однородной совокупности должны дополняться групповыми средними, характеризующими части совокупности.

В экономических исследованиях и плановых расчетах применяются две категории средних:

• степенные средние;

• структурные средние.

К категории степенных средних относятся: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая. Величины, для которых исчисляется средняя, обозначаются буквой. Средняя обозначается через. Такой способ обозначения указывает на происхождение средней из конкретных величин. Черта вверху символизирует процесс осреднения индивидуальных значении. Частота — повторяемость индивидуальных значений признака - обозначается буквой f; Σf=n.

Формулы средних величин могут быть получены на основе степенной средней, для которой определяющей функцией является уравнение

откуда

В дальнейшем при написании формул средних подстрочные значки i, n использоваться не будут, но подразумевается, что суммируются все произведения.

В зависимости от степени к получаются различные виды средних величин, их формулы представлены в табл. 4.1.

Таблица 4.0 Формулы различных видов степенных средних величин

Значение k	Наименование средней	Формула средней
		Простая	Взвешенная
-1	Гармоническая
0	Геометрическая
1	Арифметическая
2	Квадратическая
3	Кубическая

Как видно из данных табл. 4.1, взвешенные средние учитывают, что отдельные варианты значений признака имеют различную численность, поэтому каждый вариант «взвешивают» по своей частоте, т. е. умножают на нее. Частоты f при этом называются статистическими весами или просто весами средней. Однако необходимо учитывать, что статистический вес - понятие более широкое, чем частота. В качестве веса могут применяться какие-либо другие величины (в табл. 4.1 они обозначены буквой w). Например, при расчете средней продолжительности рабочего дня по предприятию единственно правильным будет взвешивание по количеству отработанных человеко-дней. Частоты отдельных вариантов могут быть выражены не только абсолютными величинами, но и относительными — частостями.

Величины степенных средних, рассчитанных на основе одних и тех же индивидуальных значений признака, при различных значениях степени (к), не одинаковы. Чем выше степень к средней, тем больше величина самой средней:

Вопрос о выборе средней решается в каждом отдельном случае, исходя из задачи исследования, материального содержания изучаемого явления и наличия исходной информации. Он состоит из нескольких этапов:

1. устанавливается определяющий показатель, т. е. обобщающий показатель совокупности, от которого зависит величина средней;

2. определяется математическое выражение для определяющего показателя;

3. производится замена индивидуальных значений среднимивеличинами;

4. решение уравнения средней.

Основополагающее правило при этом заключается в том, что величины, представляющие собой числитель и знаменатель средней, должны иметь определенный логический смысл.

Средняя арифметическая и средняя гармоническая наиболее распространенные виды средней, получившие широкое применение в плановых расчетах, при расчете общей средней из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Выбор средней арифметической и средней гармонической определяется характером имеющейся в распоряжении исследователя информации.

Средняя квадратическая применяется для расчета среднего квадратического отклонения (σ), являющегося показателем вариации признаков, а также в технике.

Средняя геометрическая (простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики, если промежутки времени, к которым относятся коэффициенты роста, одинаковы. Если средние коэффициенты роста относятся к периодам различной продолжительности, то общий средний коэффициент роста за весь период определяется по формуле средней геометрической взвешенной (— продолжительность периода, к которому относится средний коэффициент роста).