
- •Збірник задач з фізики. Механіка Модуль 1
- •Загально-теоретичні відомості. Основні визначення і формули Розділ 1. Фізичні основи механіки
- •1.1. Кінематика
- •1.2. Тангенціальне, нормальне і повне прискорення
- •1.3. Рух точки по колу. Кутова швидкість і кутове прискорення
- •Розділ 2. Динаміка матеріальної точки
- •2.1. Перший закон Ньютона (закон інерції)
- •2.2. Сила
- •2.3. Другий закон Ньютона. Імпульс
- •2.4. Третій закон Ньютона. Закон збереження імпульсу
- •Розділ 3. Робота та енергія
- •Розділ 4. Динаміка обертального руху
- •4.1. Момент сили
- •4.2. Момент інерції матеріальної точки і твердого тіла відносно нерухомої осі
- •4.3. Моменти інерції найпростіших тіл: диск, стержень, куля. Теорема Штейнера
- •4.4. Момент імпульсу
- •4.5. Основне рівняння динаміки обертального руху
- •4.6. Закон збереження моменту імпульсу
- •4.7. Кінетична енергія обертального руху
- •Розділ 5. Елементи теорії відносності
Розділ 3. Робота та енергія
Єдина міра різних форм руху називається енергією. Енергія системи тіл кількісно характеризує цю систему з погляду можливих у ній кількісних і якісних перетворень руху.
Рух є невід’ємною властивістю матерії. Тому будь-яке тіло має енергію або, як часто говорять, – запас енергії, що є мірою його руху.
Будь-яке
досить мале (елементарне) переміщення
матеріальної точки або тіла, яке рухається
поступально, можна вважати прямолінійним.
Тому елементарна робота
![]() ,
що виконується силою
,
що виконується силою
![]() при малому переміщенні
при малому переміщенні
![]() точки її прикладання, дорівнює:
точки її прикладання, дорівнює:
![]() .
(3.1)
.
(3.1)
Якщо
![]() – радіус-вектор, проведений у точку
прикладання сили, то
– радіус-вектор, проведений у точку
прикладання сили, то
![]() ,
,
![]() – скалярний добуток векторів сили
– скалярний добуток векторів сили
![]() і елементарного переміщення
і елементарного переміщення
![]() точки її прикладання. Отже формулу (3.1)
можна записати у вигляді:
точки її прикладання. Отже формулу (3.1)
можна записати у вигляді:
![]() .
(3.1')
.
(3.1')
Робота,
що виконується силою
![]() на скінченому шляху, визначається:
на скінченому шляху, визначається:
 .
(3.2)
.
(3.2)
Потужністю
![]() сили
сили
![]() називається фізична величина, яка
чисельно дорівнює роботі, що виконується
цією силою, за одиницю часу:
називається фізична величина, яка
чисельно дорівнює роботі, що виконується
цією силою, за одиницю часу:
![]() .
(3.3)
.
(3.3)
Підставляючи в цю формулу вираз (3.1) для елементарної роботи, знайдемо:
![]() ,
(3.4)
,
(3.4)
де
![]() – швидкість руху тіла.
– швидкість руху тіла.
Кінетичну енергію для поступального руху визначають за формулою:
![]() ,
(3.5)
,
(3.5)
де
![]() – маса тіла,
– маса тіла,
![]() –
швидкість
тіла.
–
швидкість
тіла.
Кінетична енергія механічної системи дорівнює сумі кінетичних енергій всіх частин цієї системи. Наприклад, для системи із матеріальних точок:
![]() ,
(3.6)
,
(3.6)
де
![]() – відповідно маса і швидкість і-тої
точки системи.
– відповідно маса і швидкість і-тої
точки системи.
Потенціальною називають ту частину механічної енергії, що залежить від взаємного розташування частинок системи та їх положення в зовнішньому полі.
Потенціальну енергію визначаємо за тією роботою, яка виконується над системою, щоб перевести її з деякого нульового положення в даний стан.
Потенціальну енергію тіла на висоті визначають:
![]() ,
якщо
,
якщо
![]() .
(3.7)
.
(3.7)
Формула потенціальної енергії сили тяжіння:
![]() .
(3.8)
.
(3.8)
Формула потенціальної енергії пружної деформації:
![]() .
(3.9)
.
(3.9)
Закон збереження енергії в механічних явищах: при всяких змінах в ізольованій консервативній системі її повна енергія залишається незмінною.
Розділ 4. Динаміка обертального руху
4.1. Момент сили
Розрізняють момент сили відносно точки і відносно осі.
Моментом
сили
![]() відносно точки обертання 0,
називається векторний добуток
радіуса-вектора
відносно точки обертання 0,
називається векторний добуток
радіуса-вектора
![]() ,
проведеного з точки 0
в точку прикладання сили, на вектор сили
,
проведеного з точки 0
в точку прикладання сили, на вектор сили
![]() :
:
![]() .
(4.1)
.
(4.1)
Вектор
![]() завжди спрямований перпендикулярно до
площини розташування векторів
завжди спрямований перпендикулярно до
площини розташування векторів
![]() і
і
![]() ,
а напрям вектора
,
а напрям вектора
![]() визначають за правилом векторного
добутку (рис. 4.1).
визначають за правилом векторного
добутку (рис. 4.1).
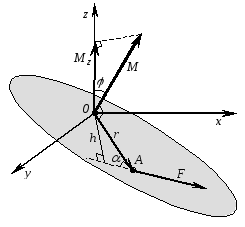
Рис. 4.1.
Модуль
вектора
![]() визначається за формулою:
визначається за формулою:
![]() ,
(4.2)
,
(4.2)
де ![]() – кут між векторами
– кут між векторами
![]() і
і
![]() ,
а
,
а
![]() – плече (перпендикуляр опущений з
точки 0
на лінію дії сили).
– плече (перпендикуляр опущений з
точки 0
на лінію дії сили).
Одиницею
вимірювання моменту сили є
![]() .
.
Якщо
лінія дії сили проходить через точку 0
то
![]() (плече) і момент сили відносно точки 0
дорівнює нулеві.
(плече) і момент сили відносно точки 0
дорівнює нулеві.
Відповідно
рис. 4.1 момент сили відносно осі (![]() )
дорівнює моменту сили відносно точки,
через яку проходить вісь, спроектованому
на цю вісь:
)
дорівнює моменту сили відносно точки,
через яку проходить вісь, спроектованому
на цю вісь:
![]() .
(4.3)
.
(4.3)
Чисельно
момент сили відносно осі дорівнює силі,
спроектованій на площину, перпендикулярну
до осі, помноженій на найкоротшу відстань
![]() (плече) між віссю і розглядуваною
проекцією сили:
(плече) між віссю і розглядуваною
проекцією сили:
![]() .
(4.4)
.
(4.4)
Якщо
вектор
![]() збігається за напрямом з віссю
збігається за напрямом з віссю
![]() ,
то його проекція дорівнює модулю вектора
,
то його проекція дорівнює модулю вектора
![]() :
:
![]() .
.
Якщо
![]() ,
то тіло не буде обертатися.
,
то тіло не буде обертатися.
