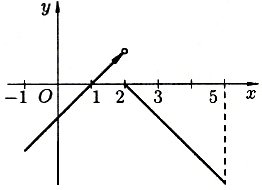Свойства функций, непрерывных на отрезке.
Для теорем этого раздела существенны оба отмеченные в названии обстоятельства: и то, что функция непрерывна, и то, что она рассматривается на замкнутом множестве - отрезке. Если не выполнены эти условия, то все теоремы перестают быть справедливыми. Напомним опр.5.1.6: функция f(x) называется непрерывной на отрезке [a,b], если она непрерывна в каждой точке этого отрезка, при этом в точках a и b предполагается непрерывность, соответственно, справа и слева.
Теорема 1 (Об обращении функции в нуль). Если функция f(х) непрерывна на отрезке [a,b] и принимает на концах этого отрезка значения разных знаков, то найдётся точка с[a,b], в которой функция обращается в нуль: f(с) =0, a<c<b.
Теорема 2 (О промежуточном значении). Если функция f(х) непрерывна на отрезке, и в двух точках a и b (a < b) принимает неравные значения A= f(а)B= f(b), то для любого числа С, лежащего между A и B, найдётся точка с[a,b], в которой значение функции равно С: f(с) = С.
Теорема 3 (Об ограниченности непрерывной функции на отрезке). Если функция f(х) непрерывна на отрезке, то она ограничена на этом отрезке.
Теорема 4 (О достижении минимального и максимального значений). Если функция f(х) непрерывна на отрезке, то она достигает на этом отрезке свои нижнюю и верхнюю грани.
Следствие
всех предыдущих
теорем: множество значений непрерывной
на отрезке [a,b]
функции заполняет весь отрезок [М*,
М*].
В дальнейшем величину
будем обозначать просто М, величину
будем обозначать символом m.
Теорема 5 (О непрерывности обратной функции). Пусть функция у= f(x) непрерывна и строго возрастает (убывает) на отрезке [a,b]. Тогда на отрезке [m,М] существует обратная функция х = g(у), также монотонно возрастающая (убывающая) на [m,М] и непрерывная.
Непрерывность функций. Практикум.
Рассмотрим примеры.
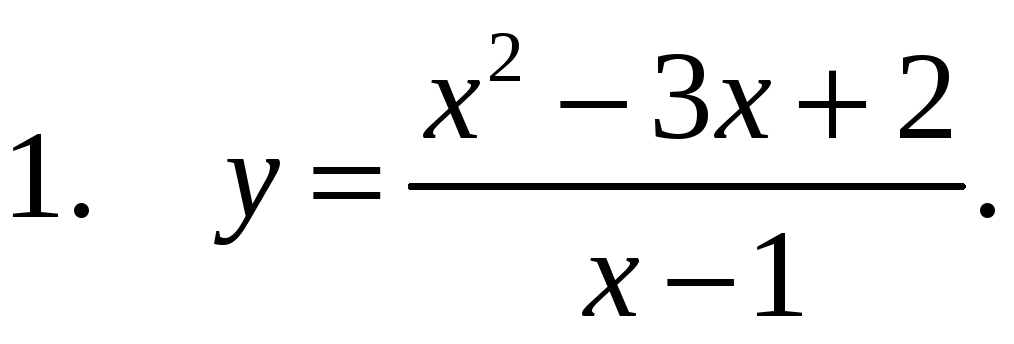
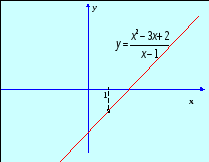
Функция не определена при х = 1, а для остальных значений аргумента может быть представлена как у = х - 2. Следовательно,
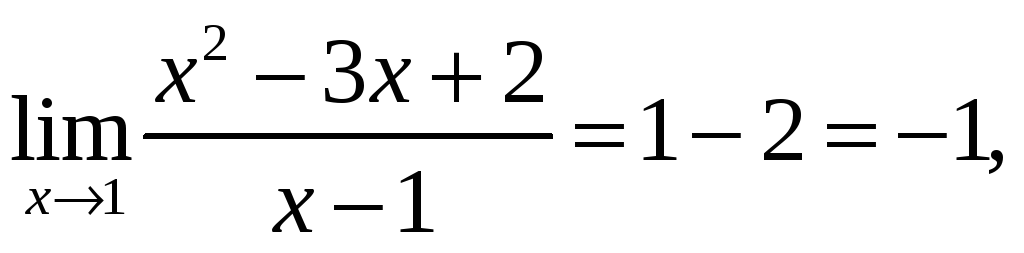
то есть х = 1 – устранимая особенность.
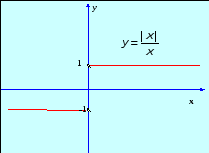
Из определения модуля следует, что у = 1 при x > 0, y = -1 при x < 0, а при х = 0 функция не определена. При этом
Следовательно, х = 0 –точка разрыва 1-го рода.
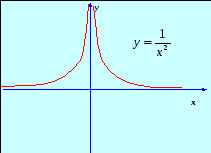
Функция не определена при х = 0 , и
Поэтому х = 0 – точка разрыва 2-го рода.
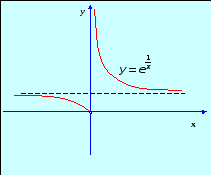
то есть правосторонний предел не является конечным. Значит, х = 0 – точка разрыва 2-го рода.
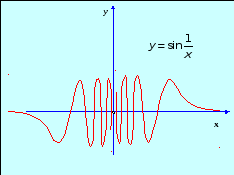
Функция не определена при х = 0 и не имеет предела при х→0. Следовательно, х = 0 – точка разрыва 2-го рода.
6.
При
каком значении числа а
функция
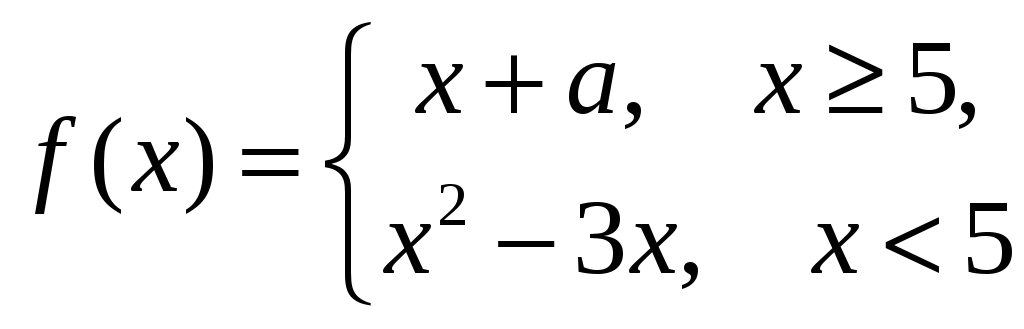
будет непрерывной?
Решение.
Областью определения функции является все множество действительных чисел, причем по обе стороны точки х = 5 функция является элементарной, то есть непрерывной. Для обеспечения непрерывности в точке х = 5 поставим условие
Ответ:
.
7.
Каким
числом можно доопределить функцию
при х
= 0, чтобы она стала непрерывной в этой
точке?
Решение.
Найдем
предел данной функции в точке х
= 0:
Следовательно, если принять f (0) = 3, функция станет непрерывной точке х = 0.
Ответ: 3.
8.
Каким
числом можно доопределить функцию
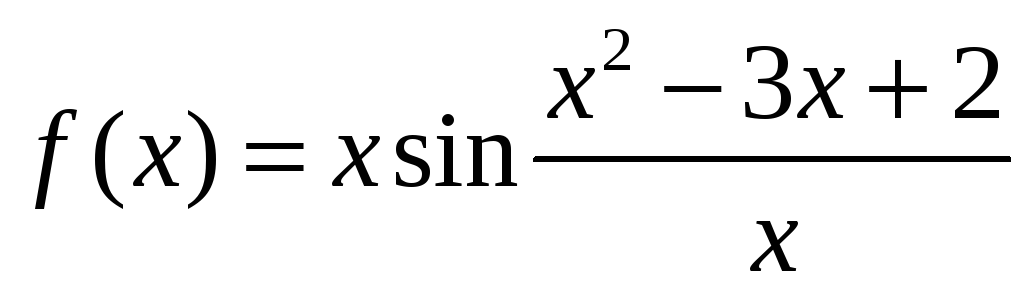при х
= 0, чтобы она стала непрерывной в этой
точке?
Решение.
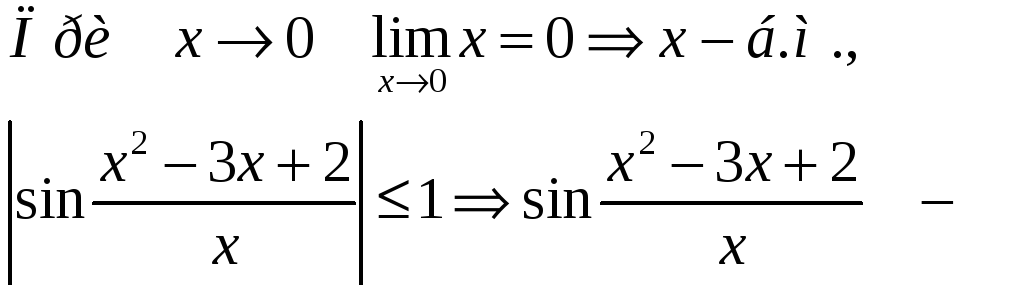
ограниченная функция. Как известно, произведение бесконечно малой функции на ограниченную есть бесконечно малая, поэтому
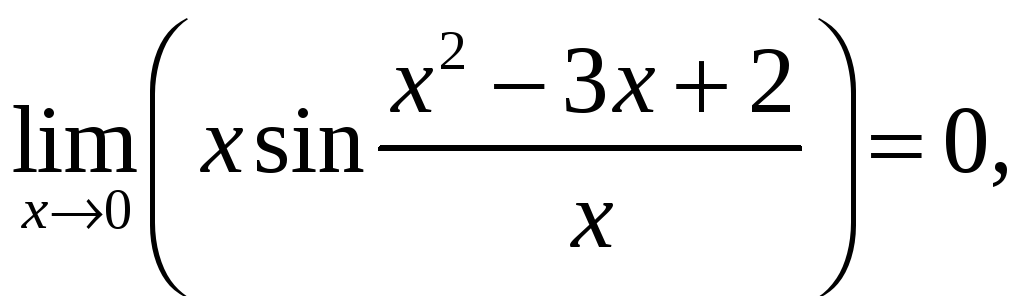
то есть предел существует и конечен. Поэтому можно доопределить функцию так: f (0) = 0.
Ответ: f (0) = 0.
9.
Каким
числом можно доопределить функцию
при х
= 0, чтобы она стала непрерывной в этой
точке?
Решение.
Найдем односторонние пределы данной функции в точке х = 0:
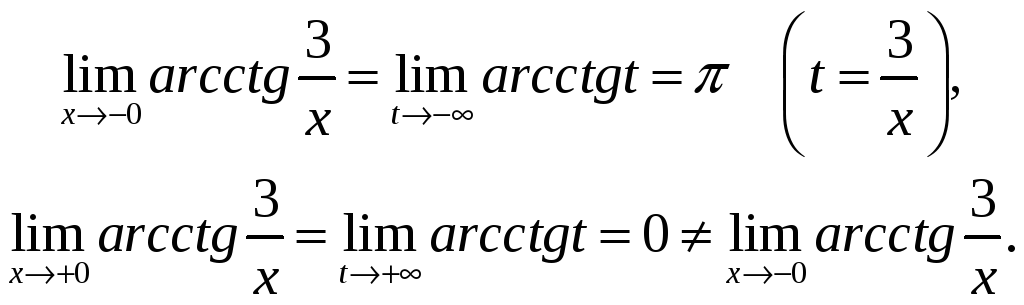
Следовательно, предел данной функции в точке х = 0 в обычном смысле не существует, поэтому добиться ее непрерывности в этой точке невозможно.
Ответ: это невозможно.
10.
Найти
количество точек разрыва функции
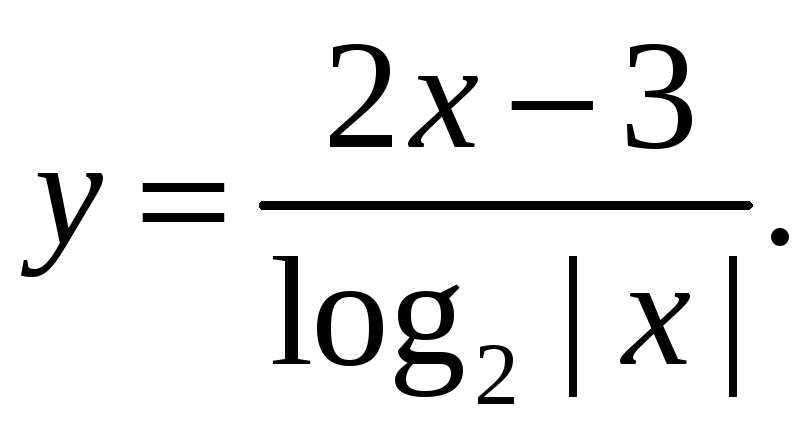
(Дополнительно: исследовать характер этих точек).
Решение.
Данная функция не существует при трех значениях аргумента: х = 0 и х = +1 (в первом случае знаменатель не существует, во втором он равен нулю). Каждая из найденных точек является внутренней точкой области определения и, следовательно, точкой разрыва.
Исследуем характер точек разрыва:
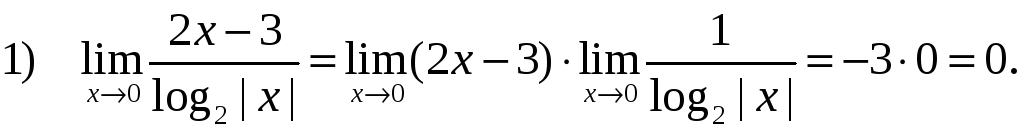
Следовательно, х = 0 – устранимая особенность.
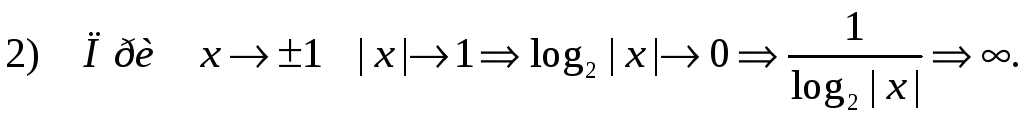
Следовательно,
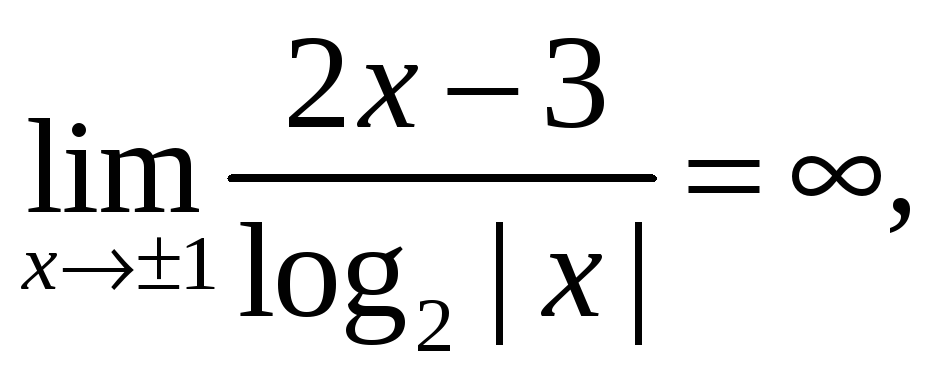
и х = +1 – точки разрыва 2-го рода.
Ответ: 3.
11.
Среди
функций
,
,
,
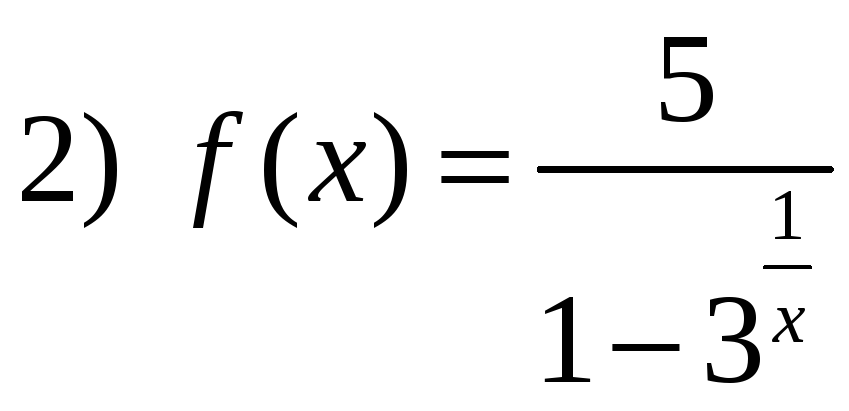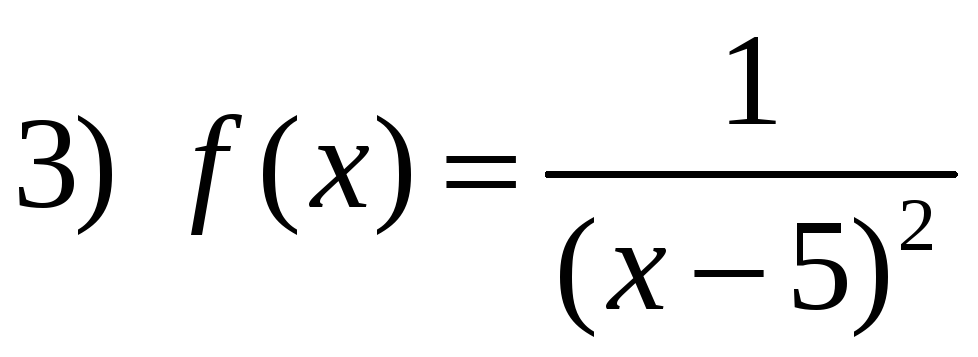точки разрыва 1-го рода имеют?
Решение.
Найдем точки разрыва каждой функции и исследуем их характер.
1)
Функция
не определена при х
= 0.
следовательно, единственная точка разрыва этой функции – это точка разрыва 2-го рода.
2)
Функция
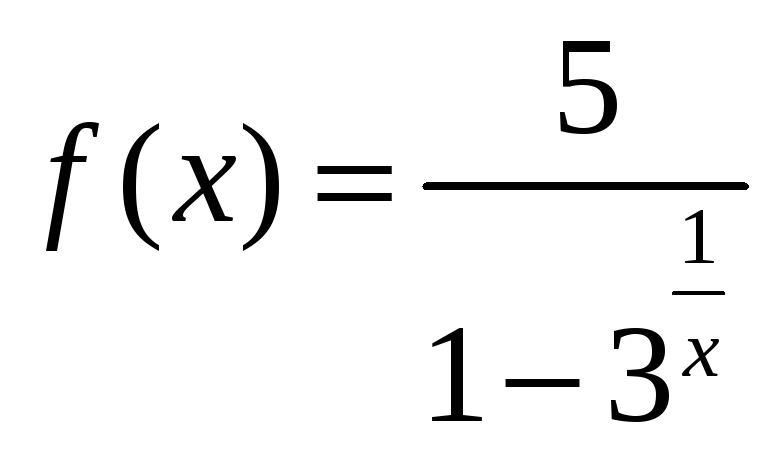не
определена при х
= 0 (заметим, что знаменатель основной
дроби не равен нулю ни при каком значении
х).
Найдем односторонние пределы f (x) в точке х = 0:
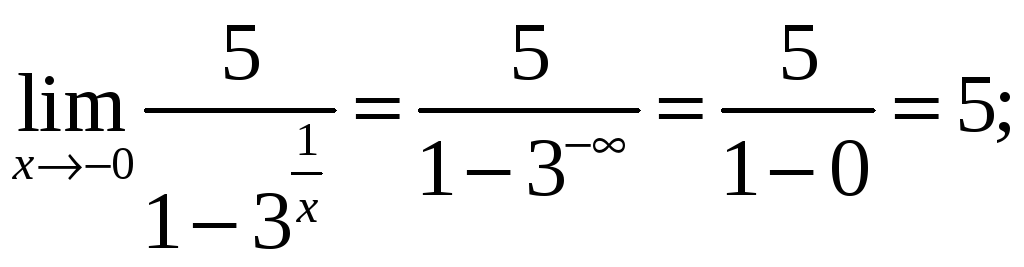
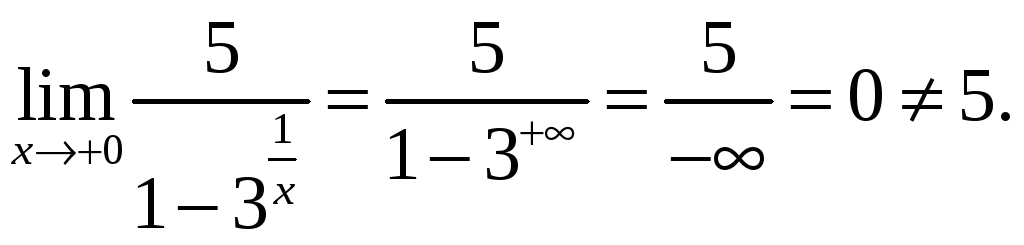
Следовательно, х = 0 – точка разрыва 1-го рода.
3)
Функция
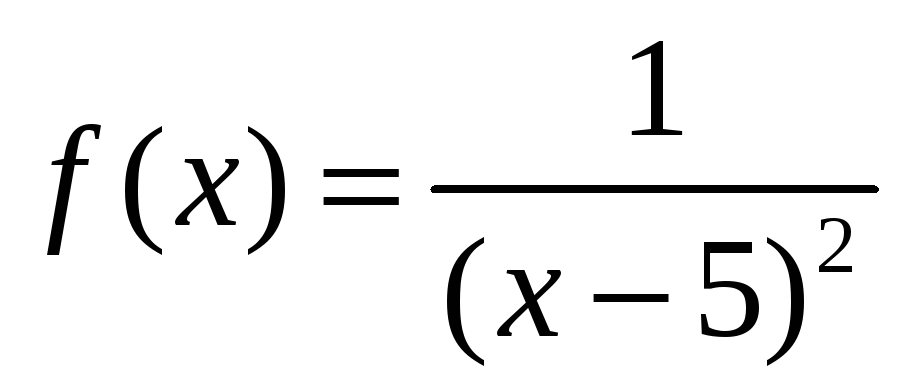не определена при х
= 5.
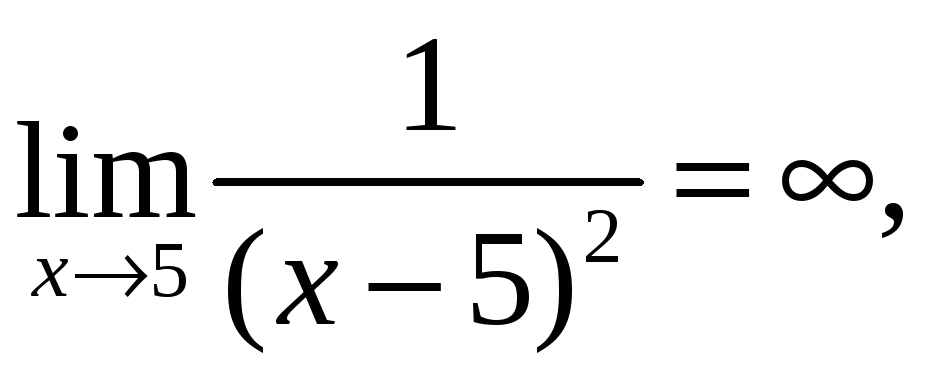
следовательно, точка х = 5 – точка разрыва 2-го рода.
4)
Функция
не определена при х
= -0,5. При этом
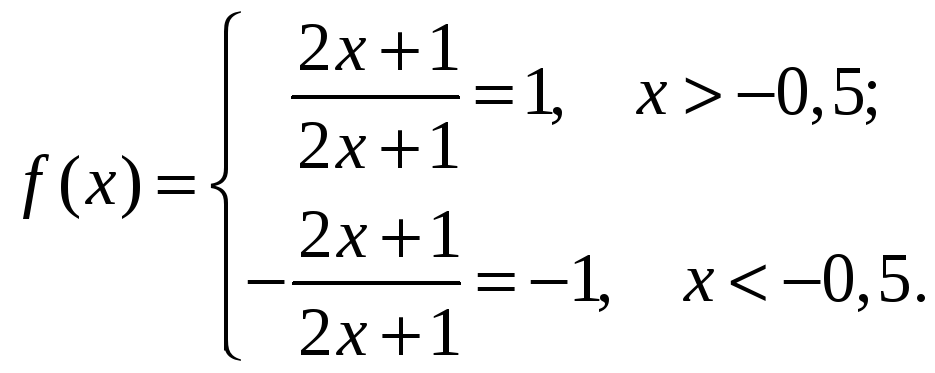
Таким образом, односторонние пределы в точке х = -0,5 равны соответственно 1 и -1, то есть эта точка – точка разрыва 1-го рода.
Ответ: 2,4.
12.
Определить значения параметров
и
,
при которых функция
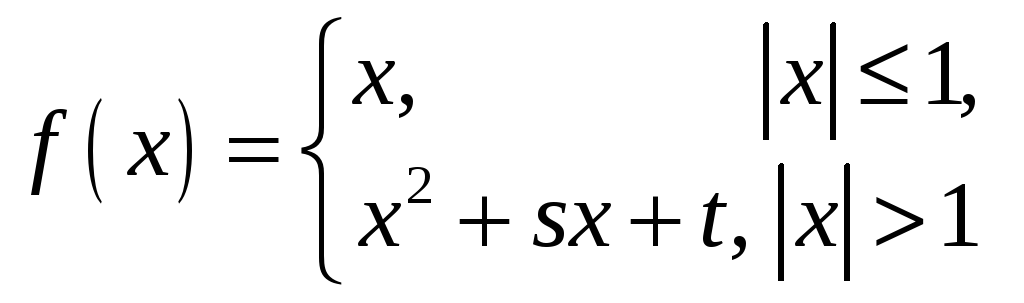непрерывна на
.
Решение.
Функция
непрерывна в точке
,
если предел справа равен пределу слева
и равен значению функции в этой точке:
.
Данная функция неэлементарная и на трех
интервалах меняет свое аналитическое
выражение: при
(
)
задана функция вида
,
на интервалах
(
и
)
функция имеет вид
(см. схему на рис. 3.1).
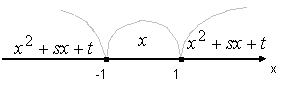
Рис. 3.1
Вычислим
односторонние пределы:
,
,
,
.
Так как для непрерывной функции выполняются условия
и
,
то, приравнивая значения односторонних пределов, получим систему
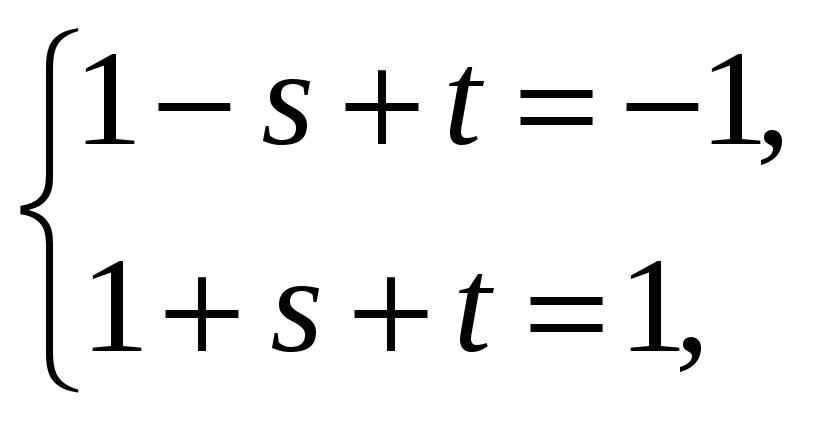
решив
которую получим
,
.
Ответ.
При
,
функция
является непрерывной.
Типы
разрывов функции в точке.
а) Пусть существуют конечные пределы
и
,
причем
=
,
но не равны
,
либо
не определена. Тогда
называется точкой устранимого разрыва
функции.
б)
Пусть
и
существуют, конечны, но не равны между
собой. Тогда в точке
у функции разрыв типа скачок.
Устранимый
разрыв и скачок называются разрывами
первого рода. Во всех остальных случаях
точка
есть точка разрыва второго рода (функция
имеет бесконечный разрыв), т. е. один
из односторонних пределов равен
или не существует.
1
Рис. 3.2
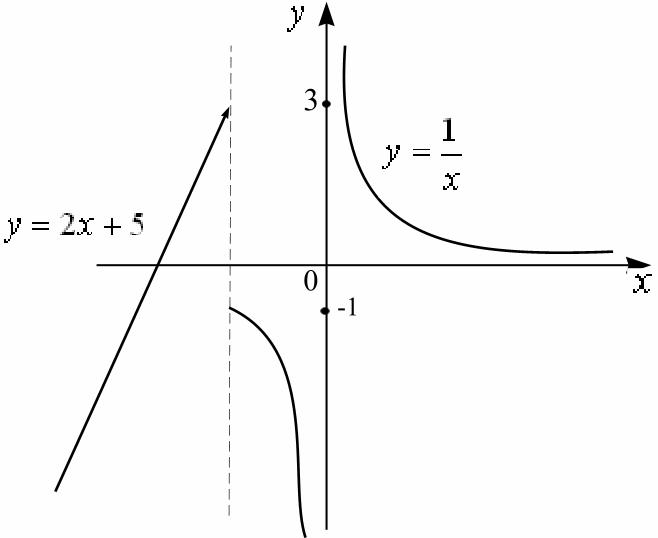
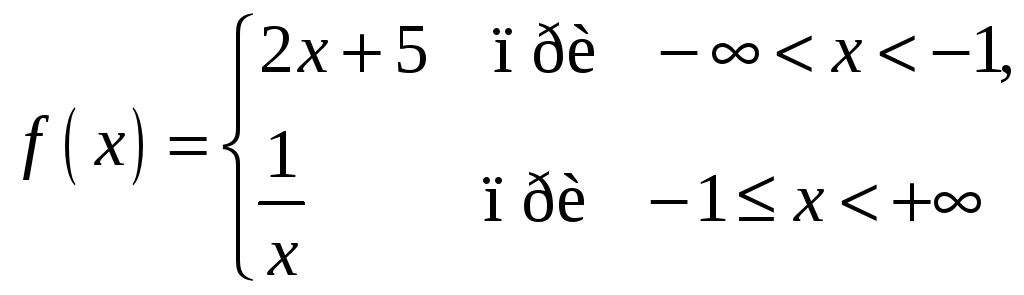и определить их характер.
Решение.
Неэлементарная
функция
определена на всей числовой оси, кроме
точки
(рис. 3.2).
Так
как
,
,
то в точке
функция терпит разрыв второго рода.
Исследуем поведение функции в точках,
где меняется аналитическое выражение
функции:
,
.
Найденные
односторонние пределы функции конечны,
но не равны между собой, поэтому в точке
функция имеет разрыв первого рода.
Скачок функции в точке разрыва равен
.
Ответ.
В точке
функция имеет разрыв первого рода, в
точке
функция терпит разрыв второго рода.
14.
Найти точки разрыва функции
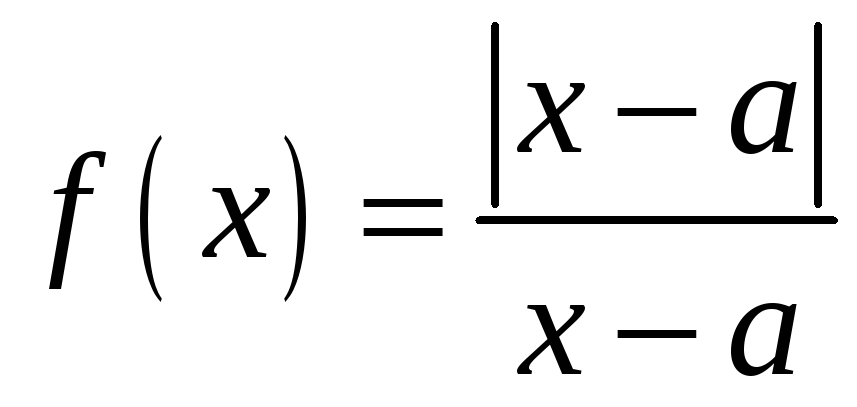и определить их характер.
Решение.
Функция
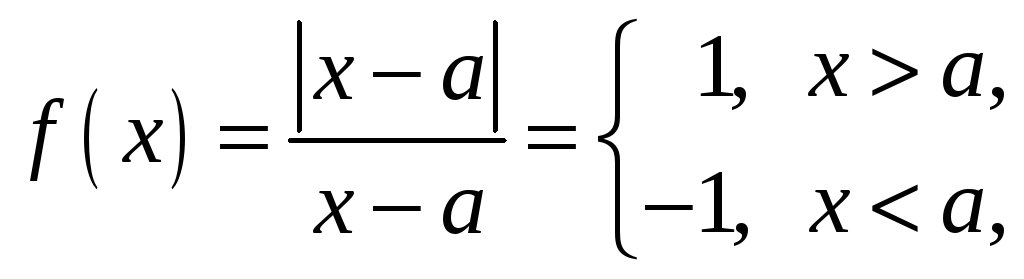следовательно, функция
определена и непрерывна на всей числовой
оси, кроме точки
.
Так как
,
,
то в точке
функция имеет разрыв первого рода.
Скачок функции в точке разрыва
равен
.
Ответ.
В точке
функция имеет конечный разрыв первого
рода.
15.
Найти точки разрыва функции
и определить их характер.
Решение.
Функция
определена для всех
таких, что
.
Так как
,
,
то в точке
функция имеет разрыв второго рода (рис.
3.3).
Ответ.
В точке
функция имеет разрыв второго рода.
16.Найти точки разрыва функции
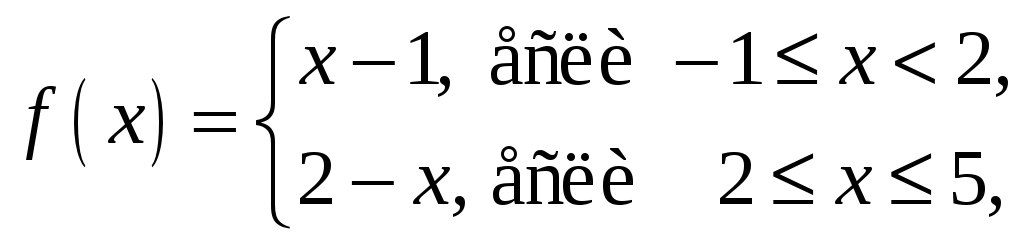и
определить их характер.
Решение.
Функция
не является элементарной и в точке
меняет свое аналитическое выражение.
Исследуем поведение функции в точке
.
Так как
и
,
то в точке
функция имеет разрыв первого рода типа
скачок (рис. 3.4).
Ответ.
В точке
функция имеет разрыв первого рода.
17. Найти точки разрыва функции
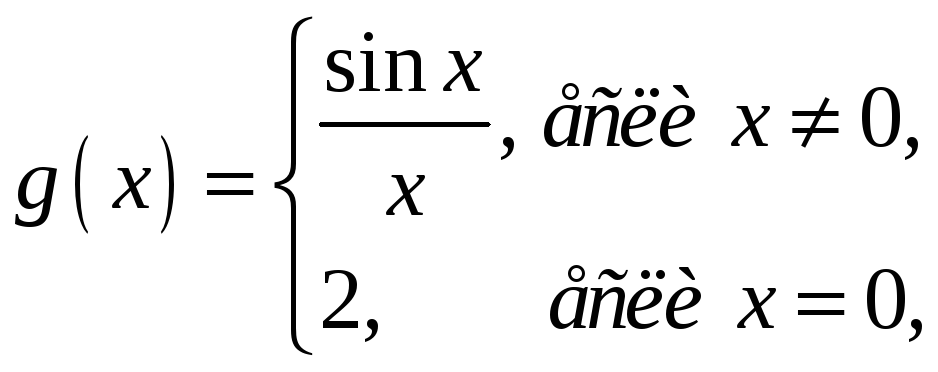и
определить их характер.
Решение.
Функция
не является элементарной и в точке
меняет свое аналитическое выражение.
Исследуем поведение функции в точке
.
Так как
и
,
то точка
является точкой устранимого разрыва
первого рода. Положив
при
,
разрыв устраним, функция станет
непрерывной (рис. 3.5).
Ответ.
Точка
является точкой устранимого разрыва
первого рода.
|
|
|
|
Рис. 3.3 Рис. 3.4 Рис. 3.5
18.
Задана
функция
и два значения аргумента
.
Требуется:
-
найти пределы функции при приближении к каждому из данных значений
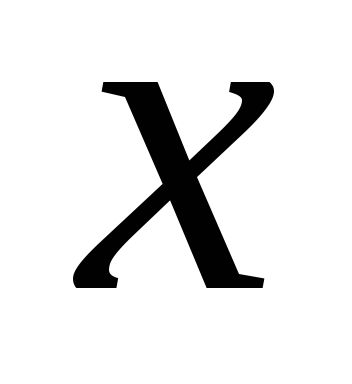слева и справа; -
установить является ли данная функция непрерывной или разрывной для каждого из данных значений
; -
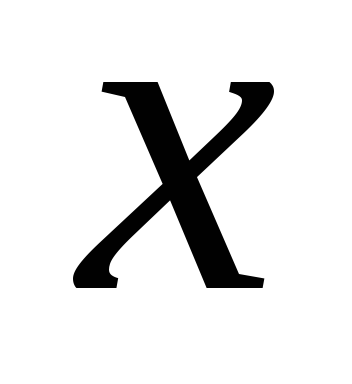сделать схематический чертеж.
Решение.
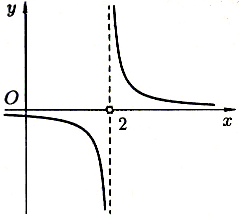
Найдем
левый и правый пределы в точке
.
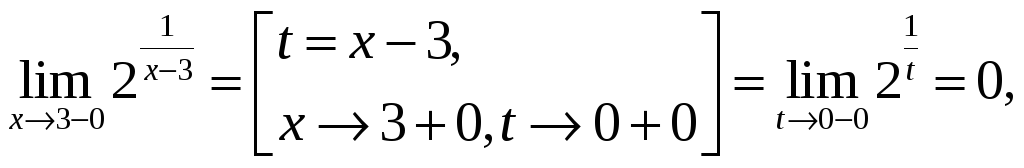
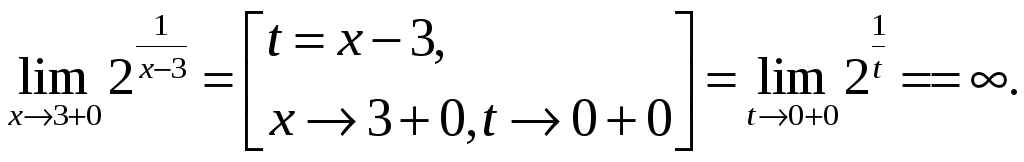
Левый
предел конечен и равен 0, а правый предел
бесконечен. Следовательно, по определению
точка разрыва второго рода.
Найдем
левый и правый пределы в точке
.
,
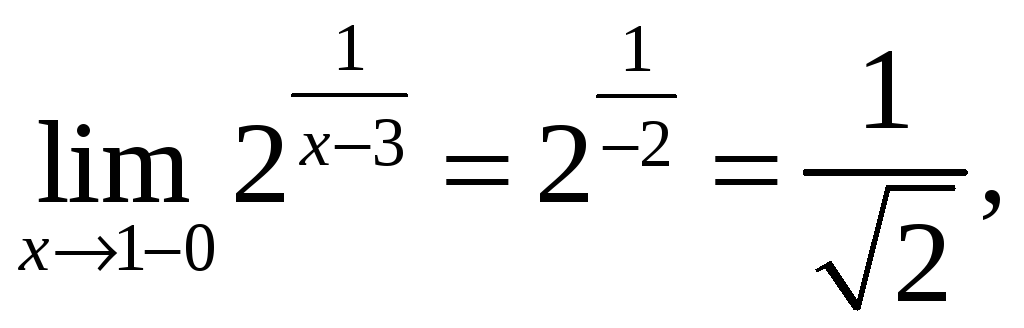
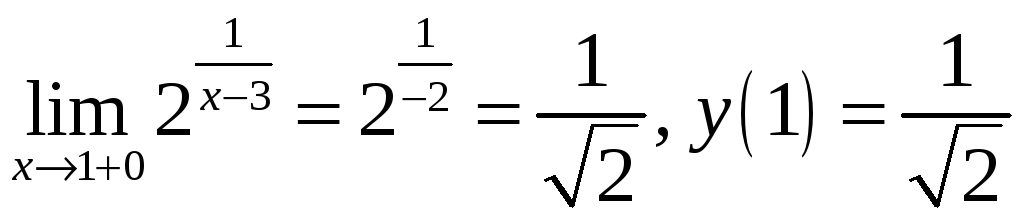т.е.
точка непрерывности функции
.
Сделаем схематический чертеж.
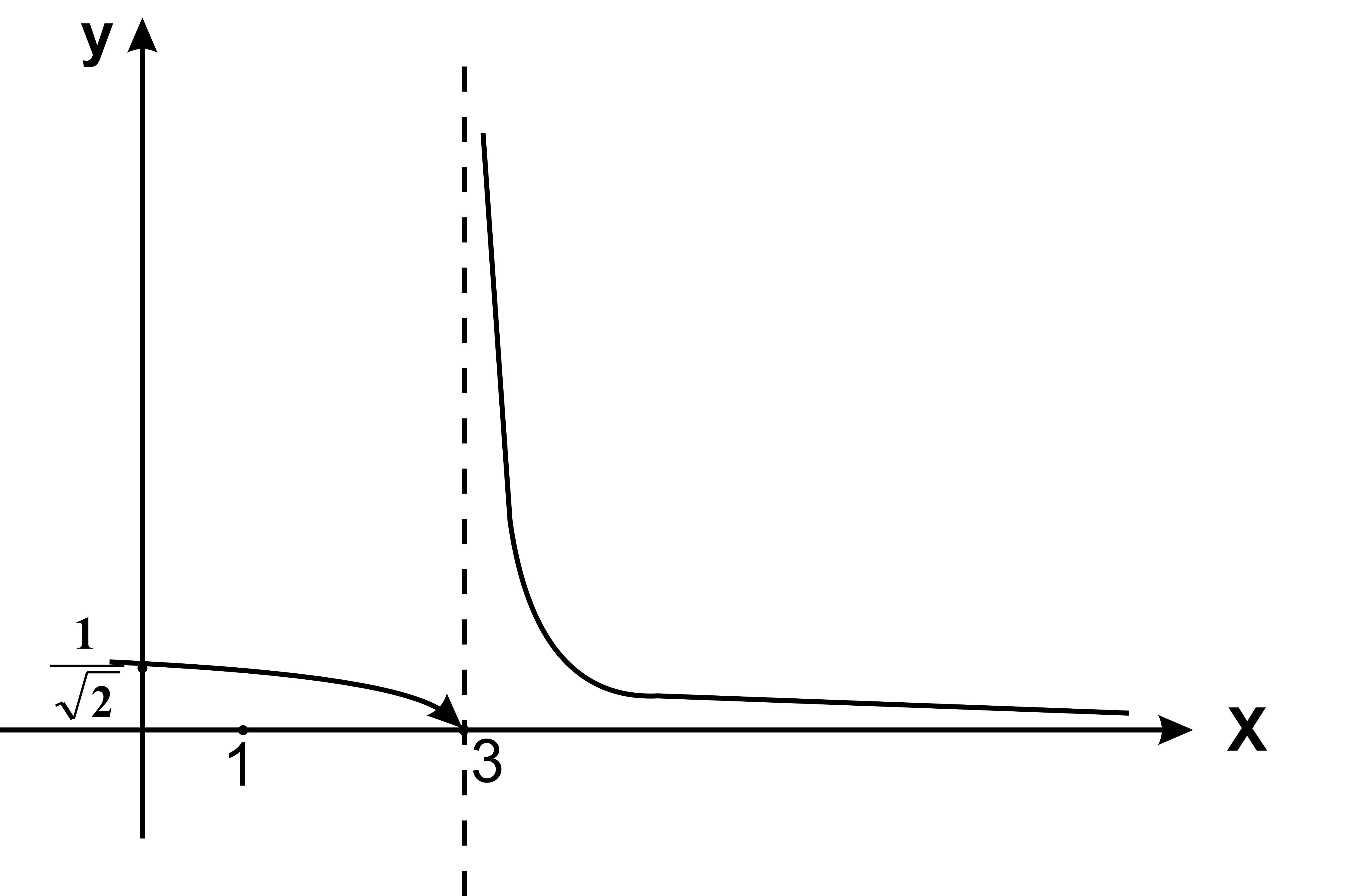
Рис. 1
19. Функция задается различными аналитическими выражениями для различных областей независимой переменной.
Требуется:
-
найти точки разрыва функции, если они существуют;
-
найти скачок функции в каждой точке разрыва;
-
сделать схематический чертеж.
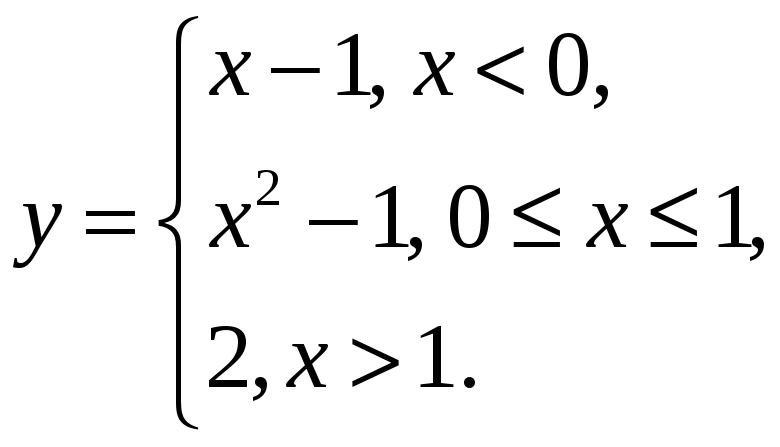
Решение.
Функция
непрерывна для
,
функция
непрерывна в каждой точке из
,
функция
непрерывна в каждой точке интервала
.
Точки,
в которых функция может иметь разрыв,
это точки
и
,
где функция меняет свое аналитическое
выражение.
Исследуем
точку
.
,
,
.
Таким образом, точка
есть точка непрерывности функции
.
Исследуем
точку
.
,
,
.
Таким образом, односторонние пределы
существуют, конечны, но не равны между
собой. По определению, исследуемая точка
– точка разрыва первого рода. Величина
скачка функции в точке разрыва
равен
.
Сделаем схематический чертеж
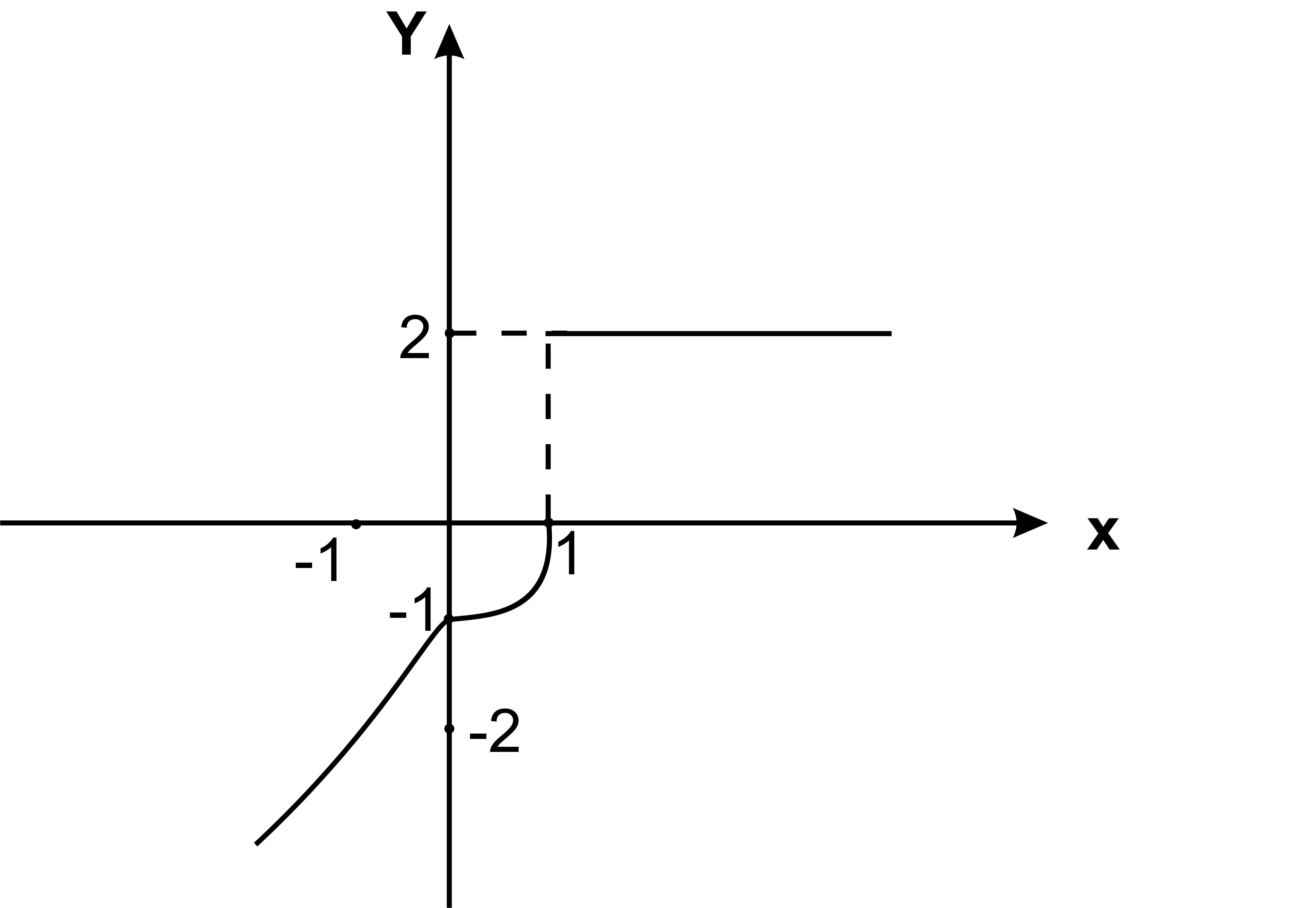
Рис. 2
Домашнее задание по теме: Непрерывность функции. Точки разрыва.
Рекомендуем решить задачи № 223– 239. Берман Г.Н. Сборник задач по курсу математического анализа, а также эти задачи.
Д1.
Указать характер точек разрыва функции
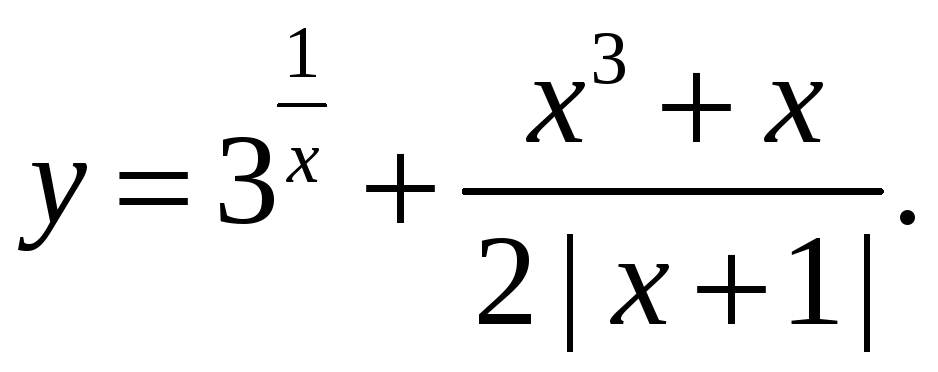
Ответ: разрыв 2-го рода и устранимая особенность
Д2.
Даны
функции
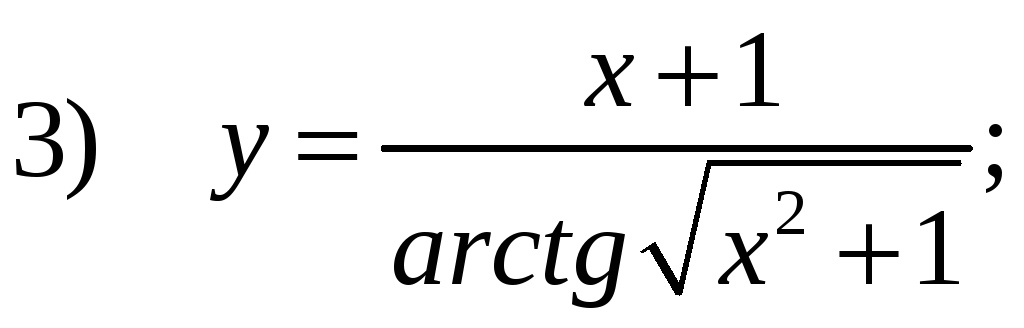
Среди них не имеет точек разрыва функция:
Ответ: 3)
Д3.
Даны
функции
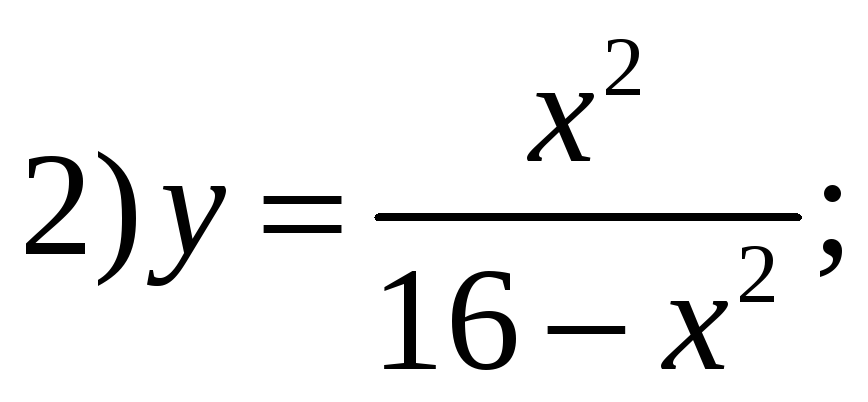
Среди них точку разрыва в виде устранимой особенности имеет функция:
Ответ: 4)
Д4.
Найти число точек разрыва функции
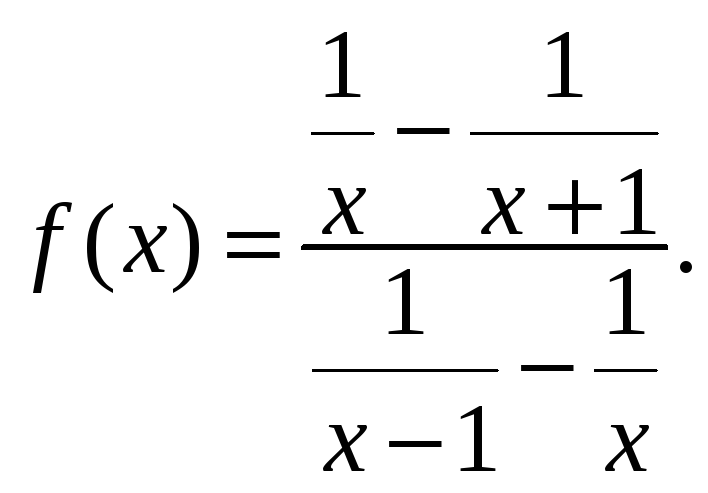
Ответ: 4
Д5.
Дана функция
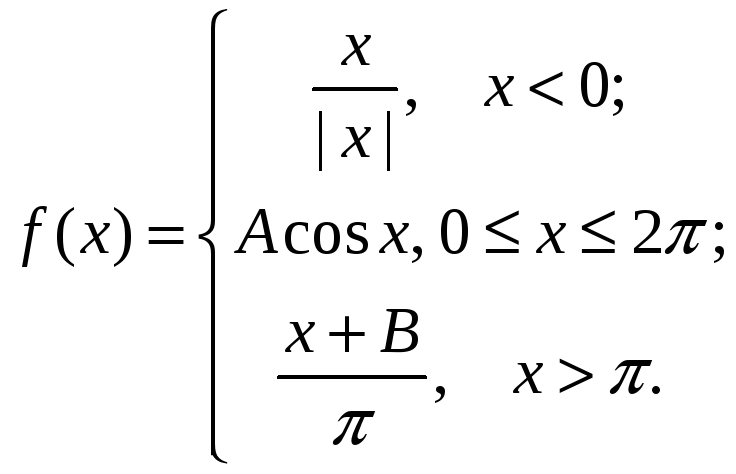
При каких А и В функция будет непрерывной?
Ответ: А = -1, В = -2
Д6.
Даны
функции
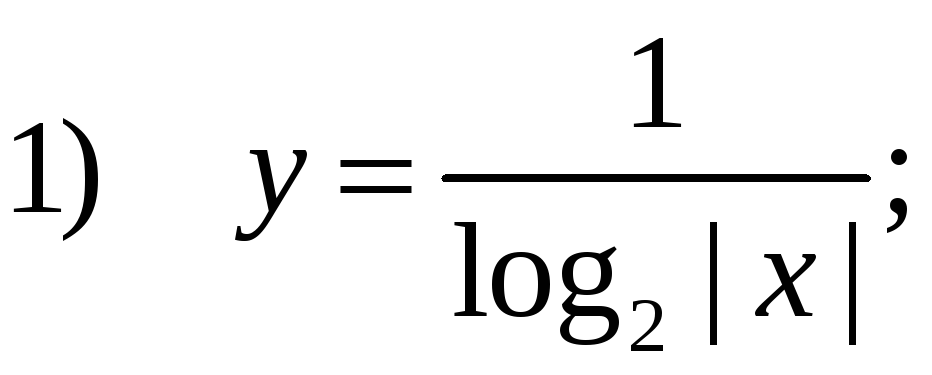
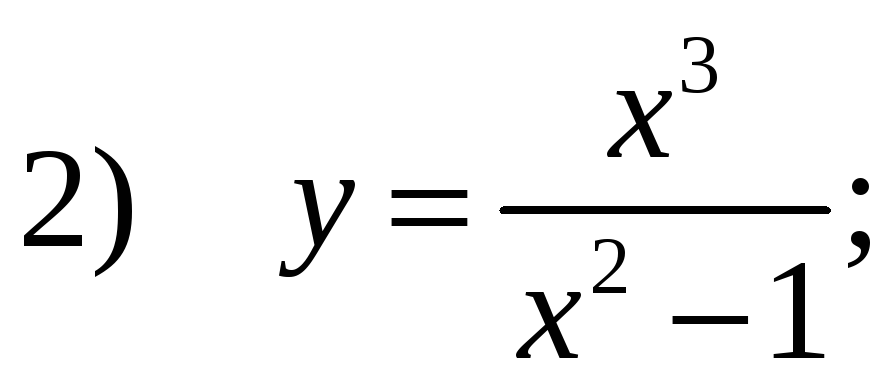
Среди них более двух точек разрыва имеет функция:
Ответ: 1)
Д7.
Если
то функция f
(x)
в точке х0:
1) непрерывна
2) имеет устранимую особенность
3) имеет разрыв 1-го рода
4) имеет разрыв 2-го рода
5) данное условие не позволяет определить поведение функции
Ответ:
Д8.
Функция
1) непрерывна при любом действительном х
2) имеет только устранимую особенность
3) имеет только разрыв 1-го рода
4) имеет только разрыв 2-го рода
5) имеет несколько точек разрыва
Ответ: 2)
Д9.
Функция
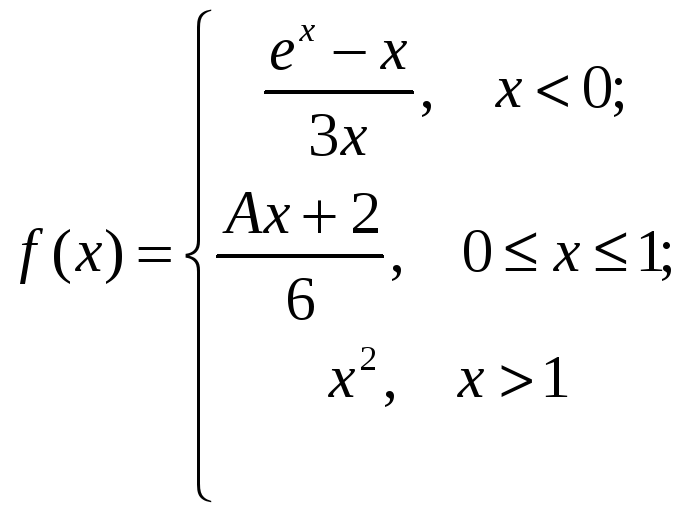
будет непрерывной при любом действительном х при А, равном:
Ответ: 4
Д10.
Функция
1) непрерывна
2) имеет устранимую особенность
3) имеет разрыв 1-го рода
4) имеет разрыв 2-го рода
5) не имеет разрыва
Ответ: 4)
Д11.
Даны
функции
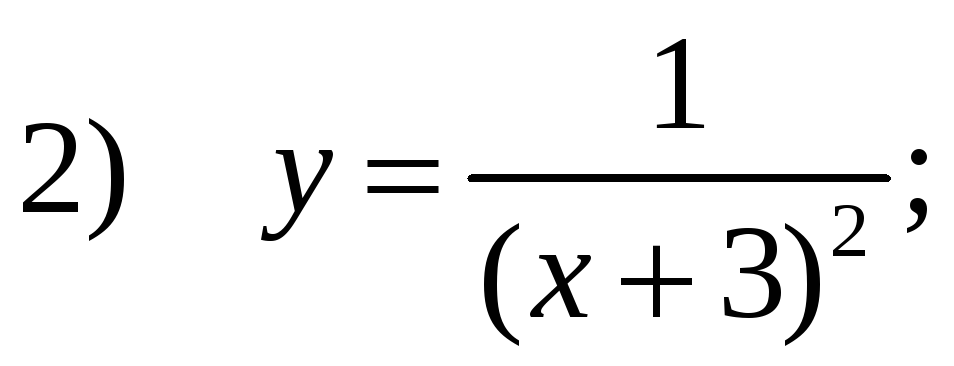
Среди них не имеет точек разрыва 2-го рода функция:
Ответ: 4)