5.4.3. Примеры разрывных функций. Исследование функций на непрерывность.

Классическими примерами разрывных функций служат функции Дирихле и Римана, определённые в разделе 4.1. Определение функции.

Функция Дирихле очевидно имеет разрывы второго рода в каждой точке, так как ни в одной точке не существует ни левого, ни правого пределов.

Относительно функции Римана

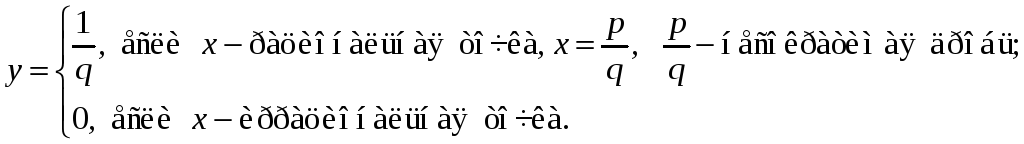
там же было доказано, что эта функция не имеет предела при х  х₀, если х₀ рационально (следовательно, каждая рациональная точка - точка разрыва второго рода), и имеет предел, равный нулю, если х₀ иррационально (следовательно, каждая иррациональная точка - точка непрерывности).

Решение задач на исследование элементарных функций на непрерывность обычно не вызывает проблем, если хорошо осмыслены определения предела и непрерывности и наработана техника нахождения пределов.

Примеры:

Исследовать функции на непрерывность:

1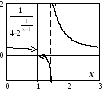. . , поэтому функция непрерывна во всех точках х0. Найдём . При х-0 1х -, arctg(1/x) -/2; при х+0 1х+, arctg(1/x) /2, т.е. не существует, но существуют односторонние пределы, следовательно, точка х=0 - точка разрыва первого рода.

2. 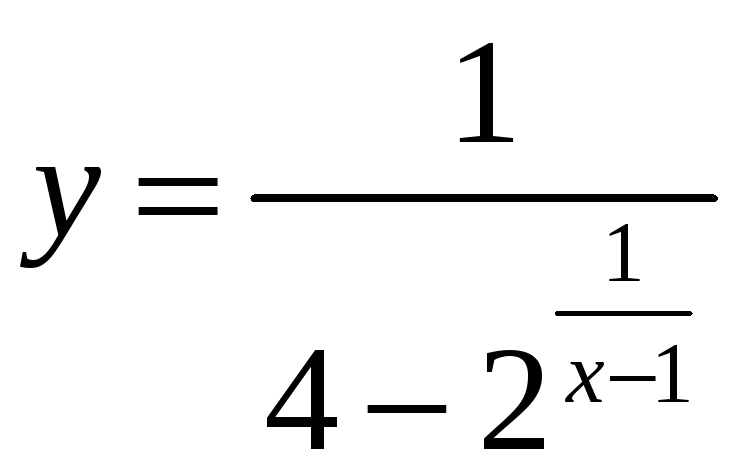. Исследовать на непрерывность надо точку х₁=1

и точки, в которых . Решая уравнение 1/(x-1)=2, находим х₂=3/2. Пусть х1-0, тогда х-1 -0, 1/(x-1)  -, 0, у1/4. Пусть х1+0, тогда х-1 +0, 1/(x-1)  +, +, у0. Пусть, далее, х3/2-0, тогда х-11/2-0, 1/(x-1) 2+0 (вследствие убывания функции 1/(x-1)), 4+0, 4- -0,

у -. Если х3/2+0, тогда х-11/2+0, 1/(x-1) 2-0, 4-0, 4- +0, у +. Если ещё убедиться, что при х и учесть монотонность функции на каждом из промежутков (-,1), (1, 3/2), (3/2,+), то полученной информации вполне достаточно для построения графика этой не самой простой функции. Результат: точка х₁=1 - точка разрыва первого рода, точка х₂=3/2 - точка разрыва второго рода.

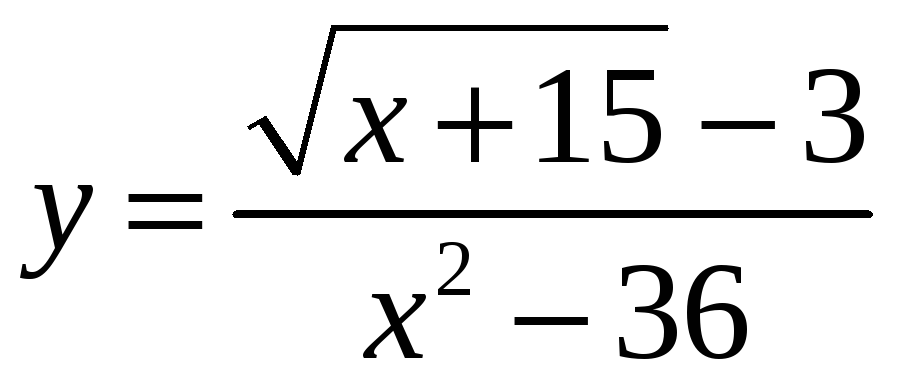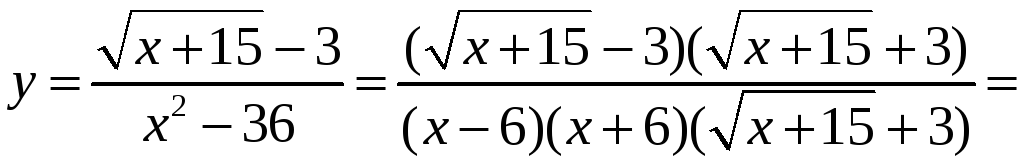
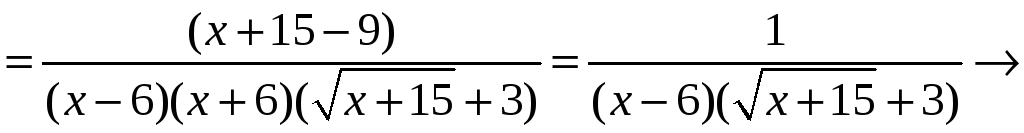
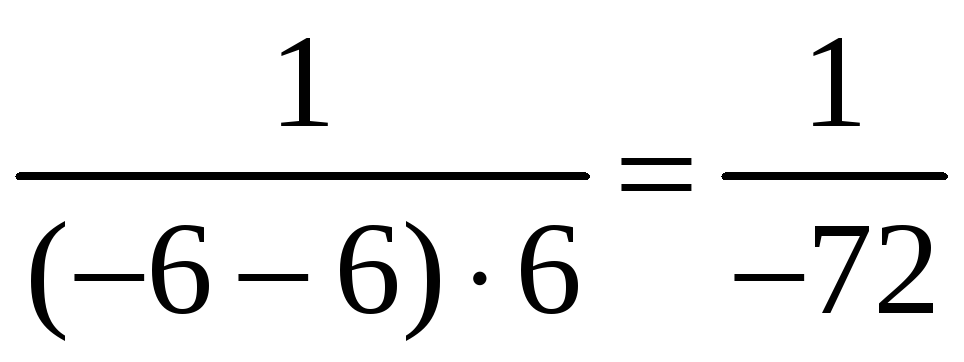3. . . Эта функция является элементарной функцией, поэтому она непрерывна во всех точках своей области определения. Исследуем точки х=6. При х+6 знаменатель стремится к нулю, числитель строго положителен, поэтому конечного предела быть не может, следовательно, это точка разрыва второго рода. При х -6 получается неопределённость , раскрываем её: при х -6. Таким образом, точка х= -6 - точка устранимого разрыва.

Непрерывность и разрывы монотонной функции.

Теорема1. Пусть функция f(x) определена на отрезке [a,b] и монотонна на этом отрезке. Тогда f(x) может иметь на этом отрезке только точки разрыва первого рода.

Следствие: если множество значений монотонно возрастающей на отрезке [a,b] функции f(х) полностью заполняет отрезок [f (a), f( b)] (т.е. для у[f (a), f( b)] х[a,b] такой, что f(х)= у), то эта функция непрерывна, легко доказать теперь от противного. Если в точке х₀ имеется скачок, то f(х) не может принимать значений, попадающих в интервал (f(х₀-0), f(х₀)).

Ещё одним следствием рассмотренных в этом разделе вопросов является непрерывность обратных тригонометрических функций.