
- •Непрерывность функций.(Теоретические сведения)
- •Арифметические операции над непрерывными функциями. Теорема о переходе к пределу под знаком непрерывной функции. Непрерывность суперпозиции функций.
- •Односторонняя непрерывность.
- •Классификация точек разрыва.
- •5.4.3. Примеры разрывных функций. Исследование функций на непрерывность.
- •Непрерывность и разрывы монотонной функции.
- •Свойства функций, непрерывных на отрезке.
ЗАНЯТИЯ 5 и 6
Непрерывность функций.(Теоретические сведения)
Определение непрерывности функции в точке.
Определение 1. Пусть функция y = f(x) определена в точке х0 и некоторой её окрестности. Функция f(x) называется непрерывной в точке х0, если:
-
существует
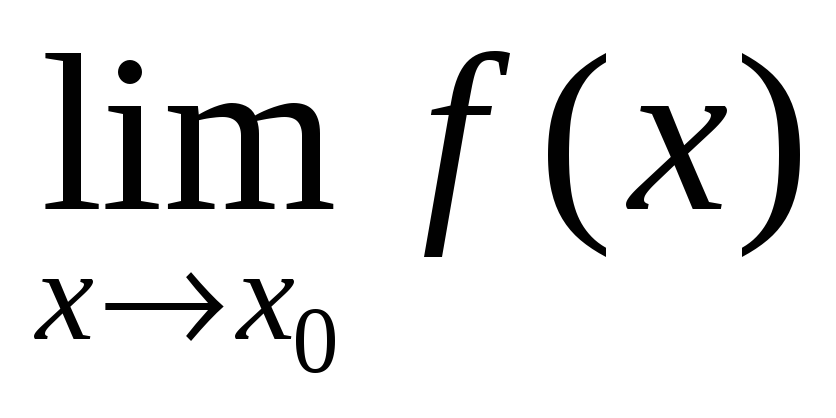 ;
; -
этот предел равен значению функции в точке х0:
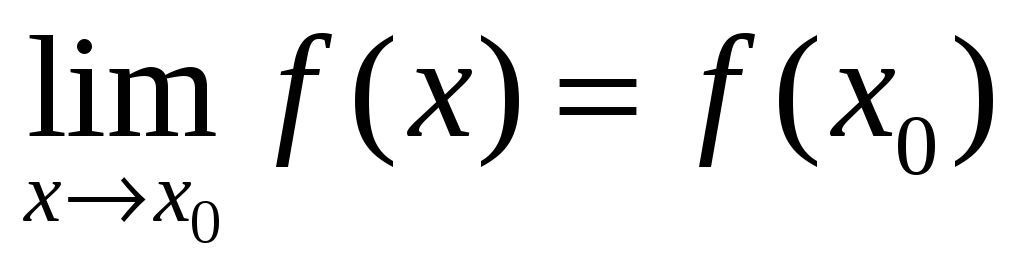 .
.
При
определении предела подчёркивалось,
что f(x)
может быть неопределена в точке х0,
а если она определена в этой точке, то
значение f(х0)
никак не участвует в определении предела.
При определении непрерывности
принципиально, что f(х0)
существует, и это значение должно быть
равно
![]() .
.
Определение 2. Пусть функция y = f(x) определена в точке х0 и некоторой её окрестности. Функция f(x) называется непрерывной в точке х0, если для 0 существует положительное число , такое что для всех х из -окрестности точки х0 (т.е. если х- х0 ) выполняется неравенство f(x) - f(х0) .
Здесь учитывается, что значение предела должно быть равно f(х0), поэтому, по сравнению с определением предела, снято условие проколотости -окрестности 0х- х0 .
Дадим ещё одно (равносильное предыдущим) определение в терминах приращений. Обозначим х=х - х0, эту величину будем называть приращением аргумента. Так как х х0, то х0, т.е. х – БМ(бесконечно малая) величина. Обозначим у = f(x) - f(х0), эту величину будем называть приращением функции, так как |у| должно быть (при достаточно малых |х|) меньше произвольного числа 0, то у - тоже БМ величина, поэтому
Определение3 .
Пусть функция y=f(x)
определена в точке х0
и некоторой её окрестности. Функция
f(x)
называется непрерывной в точке х0,
если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции.
.
Пусть функция y=f(x)
определена в точке х0
и некоторой её окрестности. Функция
f(x)
называется непрерывной в точке х0,
если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции.
Ещё одно равносильное определение на языке последовательностей:
Определение
4.
Функция f(x)
называется непрерывной в точке х0,
если для любой последовательности
![]() точек области определения, сходящейся
к х0,
последовательность соответствующих
значений функции
точек области определения, сходящейся
к х0,
последовательность соответствующих
значений функции
![]() сходится к f(х0):
сходится к f(х0):
![]() .
.
Определение 5. Функция f(x) не являющаяся непрерывной в точке х0, называется разрывной в этой точке.
Определение 6. Функция f(x) называется непрерывной на множестве Х, если она непрерывна в каждой точке этого множества.
Арифметические операции над непрерывными функциями. Теорема о переходе к пределу под знаком непрерывной функции. Непрерывность суперпозиции функций.
Теорема
1. (О
непрерывности суммы, произведения,
частного).
Пусть функции f(x),
g(x)
непрерывны в точке х0.
Тогда в этой точке непрерывны функции
f(x)g(x),
f(x)g(x),
![]() (частное - в случае, когда g(х0)0).
(частное - в случае, когда g(х0)0).
Теорема
2 (О
переходе к пределу под знаком непрерывной
функции). Пусть
функция
![]() определена в некоторой окрестности
точки t0
и имеет
определена в некоторой окрестности
точки t0
и имеет
![]() ,
равный х0.
Пусть точка
,
равный х0.
Пусть точка
![]() принадлежит области определения функции
y
= f(x),
и f(x)
непрерывна в точке х0.
принадлежит области определения функции
y
= f(x),
и f(x)
непрерывна в точке х0.
Тогда
существует![]() ,
и
,
и
![]() .
.
Теорема
3 (О
непрерывности суперпозиции непрерывных
функций).
Пусть функция
![]() непрерывна в точке точке t0.
Пусть точка
непрерывна в точке точке t0.
Пусть точка
![]() принадлежит области определения функции
y
= f(x),
и f(x)
непрерывна в точке х0.
Тогда сложная функция
принадлежит области определения функции
y
= f(x),
и f(x)
непрерывна в точке х0.
Тогда сложная функция
![]() непрерывна в точке t0.
непрерывна в точке t0.
Непрерывность элементарных функций.
Любая элементарная функция непрерывна в любой точке своей области определения.
1. Постоянная функция y(х) = C = const, очевидно, непрерывна в любой точке (предел постоянной функции равен этой постоянной в любой точке).
-
Функция y(х)= х непрерывна в любой точке х ( для 0 возьмём = , тогда если х- х0, то f(х)- f(х0) = х- х0=).
-
Функция y(х)= х2 = х х непрерывна в любой точке х как произведение двух непрерывных функций.
-
По индукции функция y(х)= хn = хn-1 х непрерывна в любой точке х как произведение двух непрерывных функций. По той же причине непрерывна функция y(х)= аnхn, где аn=C=const.
-
Рациональная функция
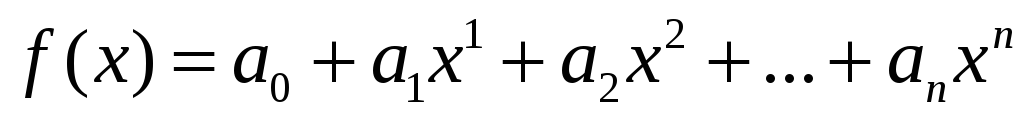 непрерывна в любой точке х
как сумма непрерывных функций.
непрерывна в любой точке х
как сумма непрерывных функций.
6.
Дробно-рациональная
функция:
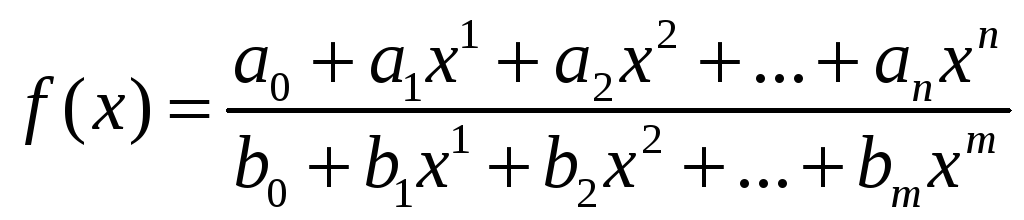 непрерывна в любой точке х,
в которой знаменатель отличен от 0, как
частное непрерывных функций.
непрерывна в любой точке х,
в которой знаменатель отличен от 0, как
частное непрерывных функций.
-
Показательная функции
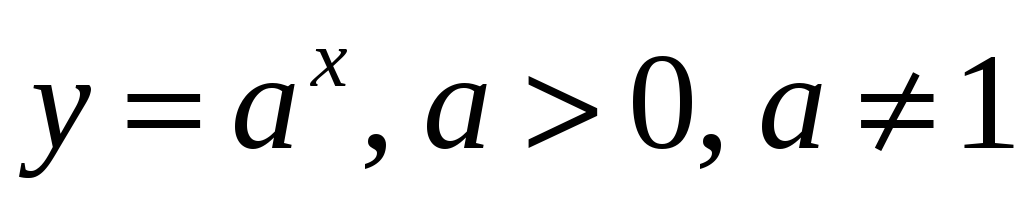 - непрерывна.
- непрерывна.
-
Логарифмическоая функция
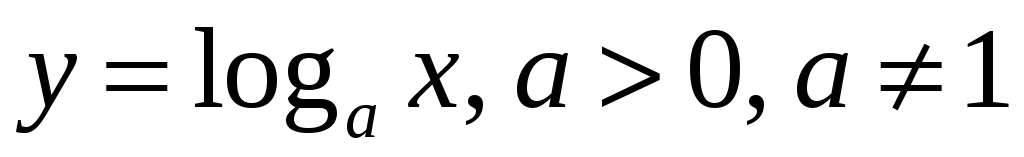 -
непрерывна.
-
непрерывна. -
Тригонометрические функции:
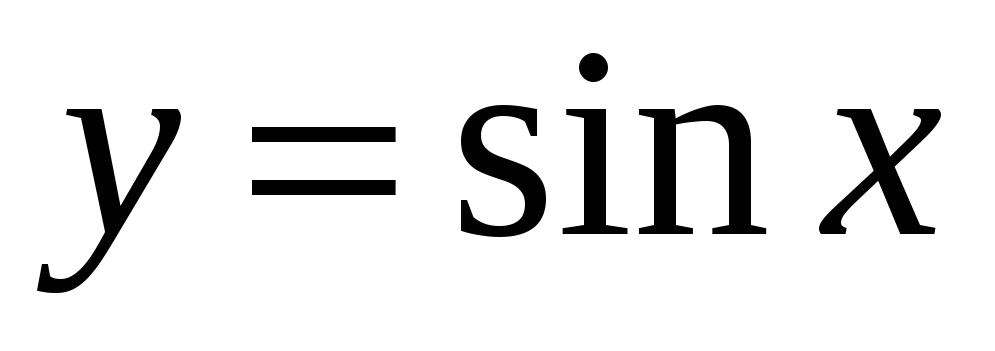 ,
,
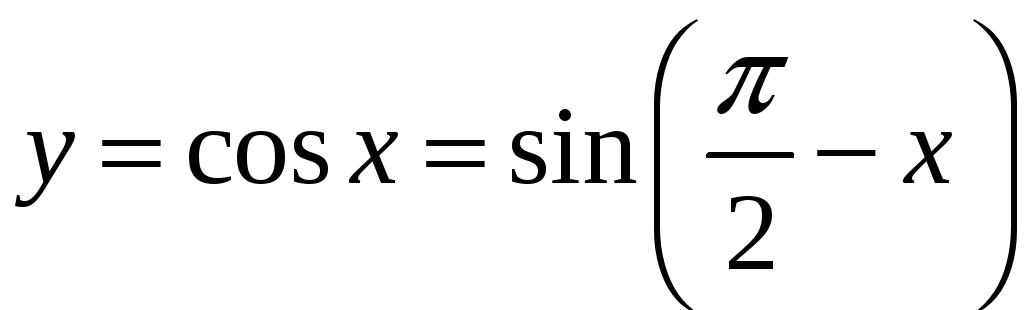 ,
,
 и
и
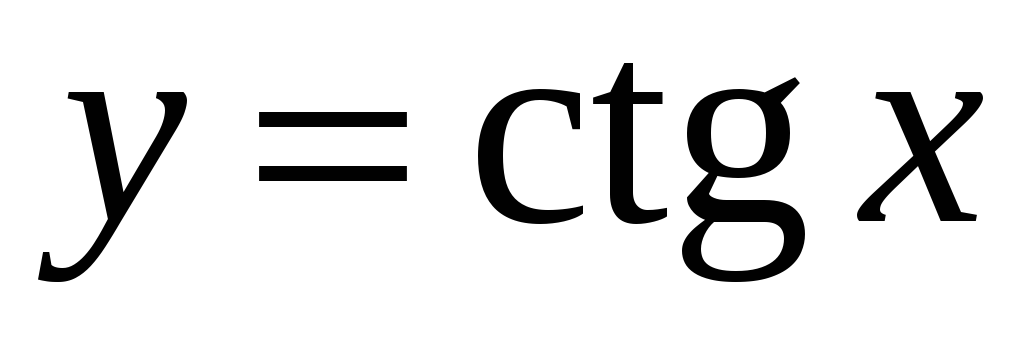 непрерывны
в точках, в которых они определены, как
частное непрерывных функций.
непрерывны
в точках, в которых они определены, как
частное непрерывных функций. -
Гиперболические функции непрерывны (
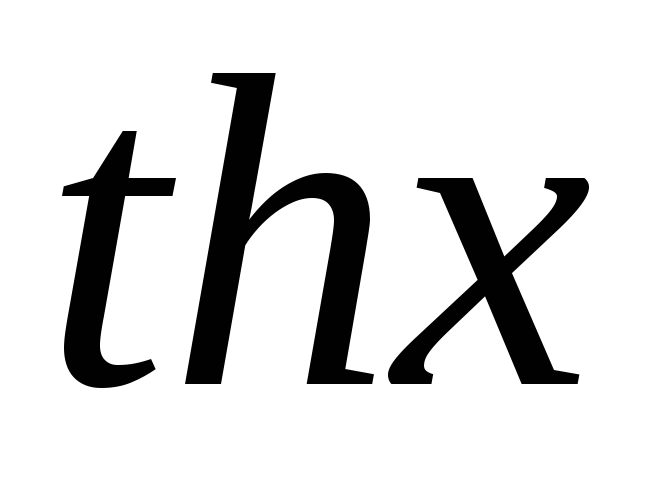 в точках, в которых
в точках, в которых
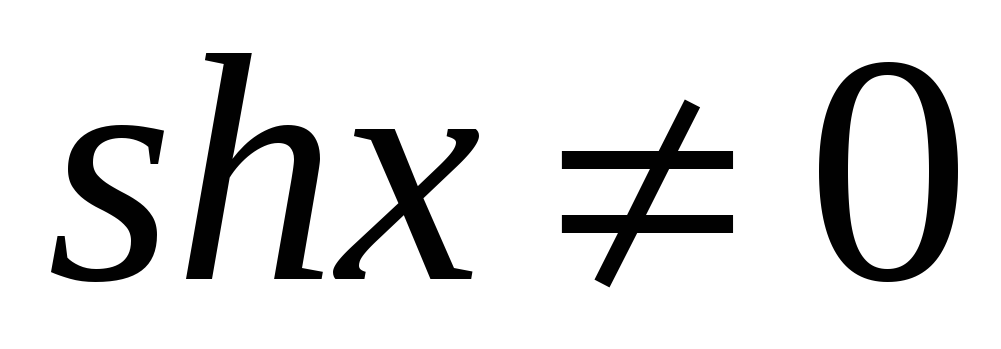 ),
так как они определяются через непрерывную
функцию
),
так как они определяются через непрерывную
функцию
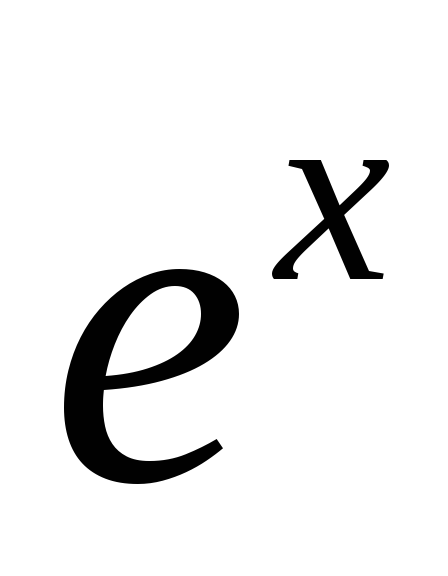 .
Обратные гиперболические функции
непрерывны , так как они выражаются
через непрерывную функцию
.
Обратные гиперболические функции
непрерывны , так как они выражаются
через непрерывную функцию
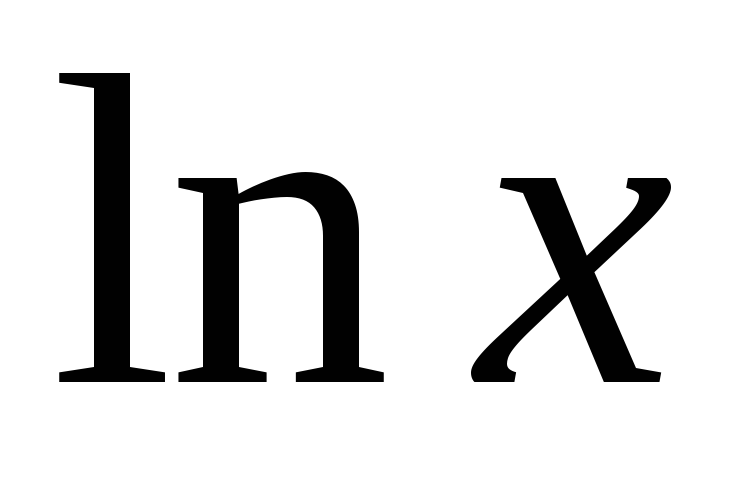 .
. -
Показательно-степенная функция
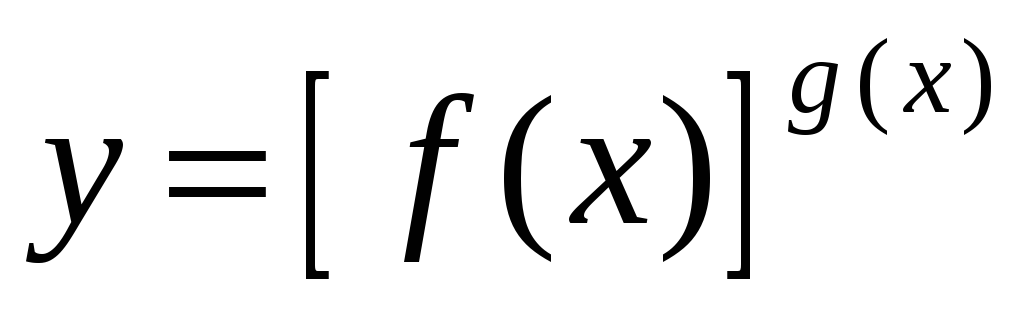 ,
,
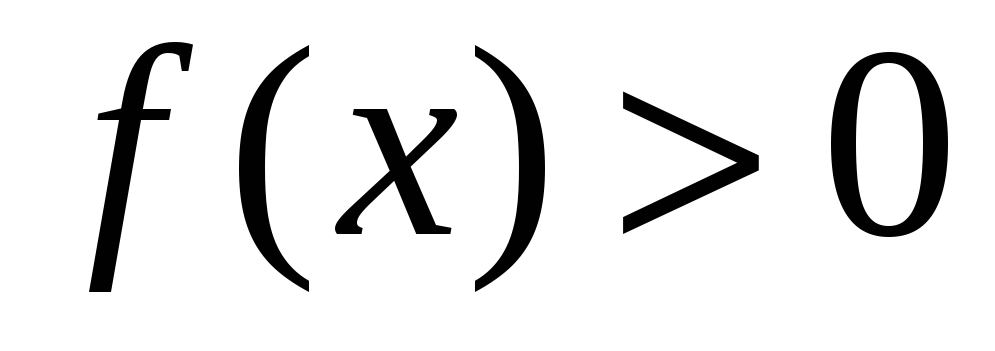 -
непрерывна, так как она представляется
в виде
-
непрерывна, так как она представляется
в виде
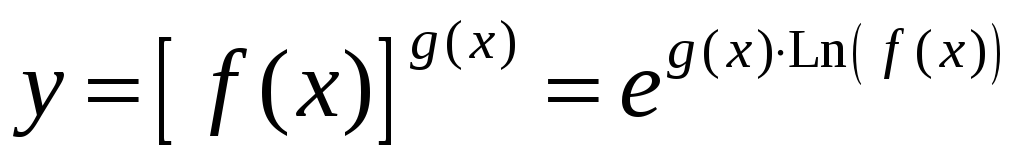 ,
т.е. в виде суперпозиции непрерывных
показательной и логарифмической
функций.
,
т.е. в виде суперпозиции непрерывных
показательной и логарифмической
функций.
