8.4. Визначення основних розмірів кулачкового механізму

До основних розмірів кулачкового механізму відносяться: мінімальний радіус кулачка та зміщення для механізму зі штовхачем; мінімальний радіус кулачка та міжосьова відстань для механізму з коромислом.

Кут тиску. Кут між нормаллю n-n у точці дотику взаємодіючих профілів вищої пари та вектором швидкості точки дотику вихідної ланки називається кутом тиску. При проектуванні механізмів з вищими парами величина цього кута має суттєве значення.

Розглянемо кулачковий механізм зі штовхачем (рис. 8.4). Якщо знехтувати силою тертя у вищій кінематичній парі, то можна вважати, що сила тиску, з якою кулачок 1 діє на штовхач 2, направлена по спільній нормалі n-n в точці дотику ланок. Гострий кут, що утворений напрямом сили тиску кулачка на штовхач і вектором швидкості штовхача називається кутом тиску . Зауважимо, що кут тиску є величиною змінною. Кут, що доповнює кут тиску до 90⁰, називається кутом передачі (руху) ().

Розкладемо силу за двома напрямками: по лінії руху штовхача та перпендикулярно до неї . Сила - корисна сила, яка рухає штовхач; сила - викликає перекошування штовхача в напрямній 3, внаслідок чого збільшуються реакції та сила тертя. Зрозуміло, що кулачковий механізм буде працювати тим краще, чим менший кут тиску. Не важко показати, що миттєвий коефіцієнт корисної дії кулачкового механізму зменшується зі зростанням кута тиску. При збільшенні кута тиску до деякого значення, що називається критичним , виникає явище заклинювання (самогальмування). Для нормальної роботи кулачкового механізму, кут тиску при будь-якому положенні кулачка має бути меншим за допустимий кут тиску, тобто .

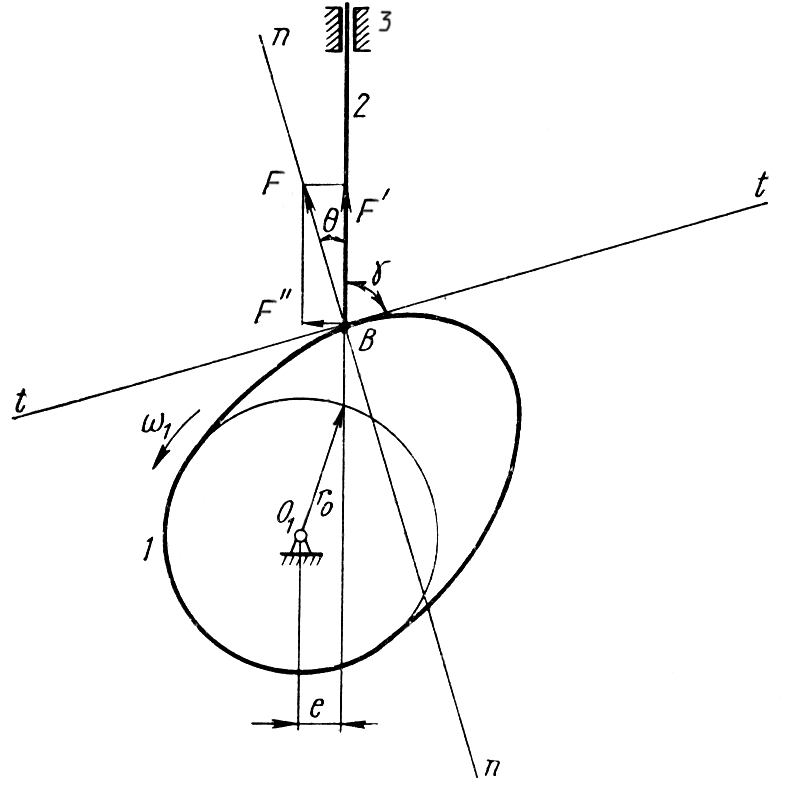
Рис. 8.4

Кут тиску можна виразити через геометричні параметри кулачкового механізму

, (8.1)

де – переміщення; ‑ аналог швидкості штовхача, що відповідає куту повороту кулачка від початку фази віддалення; e ‑ зміщення напрямної штовхача відносно центра кулачка. Відмітимо, якщо при русі штовхача на фазі віддалення вгору вздовж напрямної, остання зміщена відносно центра кулачка праворуч, то при його обертанні проти стрілки годинника зміщення підставляється в (8.1) зі знаком плюс, а при обертанні за годинниковою стрілкою - мінус. При зміщенні напрямної ліворуч від центра обертання кулачка знак змінюється на протилежний.

Подібною формулою виражається залежність між кутом тиску та основними параметрами коромислового кулачкового механізму.

Аналіз цих залежностей свідчить, що при вибраному законі руху та зміщенні можна зменшити кути тиску, збільшуючи мінімальний радіус кулачка, тобто габарити механізму. Аналогічно для коромислового кулачкового механізму кути тиску зменшуються при збільшенні , тобто розмірів механізму.

Отже, при проектуванні кулачкових механізмів основні розміри ‑ або , визначаються з умови незаклинювання механізму. Виняток становить тарілчастий кулачковий механізм, для якого (найпоширеніший випадок тарілки, перпендикулярної до напрямної) і r₀ визначається з умови опуклості контуру .

Таким чином, одним із найважливіших питань при проектуванні кулачкових механізмів є вибір допустимого кута тиску , від величини якого залежить розподіл сил у механізмі, його К.К.Д., габаритні розміри і т. ін.

Рекомендовані такі значення допустимого кута тиску: =30⁰…40⁰ для механізмів зі штовхачем; =45⁰…50⁰ для коромислових механізмів. Якщо габарити механізмів дозволяють, то для зменшення втрат на тертя доцільно приймати менші значення кута тиску.

Визначення основних розмірів кулачкових механізмів за заданим допустимим кутом тиску. Аналітичний метод визначення основних розмірів кулачкових механізмів із штовхачем (з вістрям або роликом) полягає у розв’язку рівняння (8.1) відносно шуканих параметрів при . В основі графічного методу також лежить залежність (8.1).

Розглянемо задачу графічного визначення мінімального радіуса кулачка для механізму, зображеного на рис. 8.4.

Зауважимо, що у випадку механізму з роликовим штовхачем усі побудови є аналогічними, але в результаті буде знайдений не дійсного, а центрового профілю кулачка.

Спочатку на основі попередньо побудованих графіків , шляхом виключення параметра , будуємо графік , забезпечивши чисельно однакові масштаби по обох осях, (рис. 8.5). Для цього проводимо осі прямокутної системи координат. По осі ординат, в масштабі , відкладемо від початку координат, згідно з графіком переміщення штовхача (т. А₀ відповідає нижньому початковому положенню штовхача, лежить на колі мінімального радіуса). Через отримані точки А₀, А₁, А₂, …, проводимо прямі, паралельні осі абсцис та відкладаємо на них у масштабі , відрізки, що рівні . Причому для фази віддалення ці відрізки відкладаються на напрямком обертання кулачка, а для фази опускання – обернено. Сполучивши плавною кривою кінці відкладених відрізків, отримаємо криву . Після цього проводимо до кривої дотичні прямі І-І та ІІ-ІІ під кутами до осі ординат. Центр обертання кулачка може знаходитись у будь-якій точці заштрихованої області (між дотичними), у цьому випадку завжди буде забезпечене виконання умови . Відмітимо, що точка О перетину дотичних визначає мінімально можливе значення , тобто, найменші розміри кулачка та всього механізму, при якомусь певному .

Якщо величина зміщення задана , то проводять пряму y-y на відстані від осі ординат (в масштабі ). У цьому випадку мінімальний радіус дорівнює відрізку А₀О₂ у прийнятому масштабі. У випадку центрального кулачкового механізму () центр обертання кулачка буде знаходиться на продовженні лінії руху штовхача, нижче точки О₁, а найменший радіус .

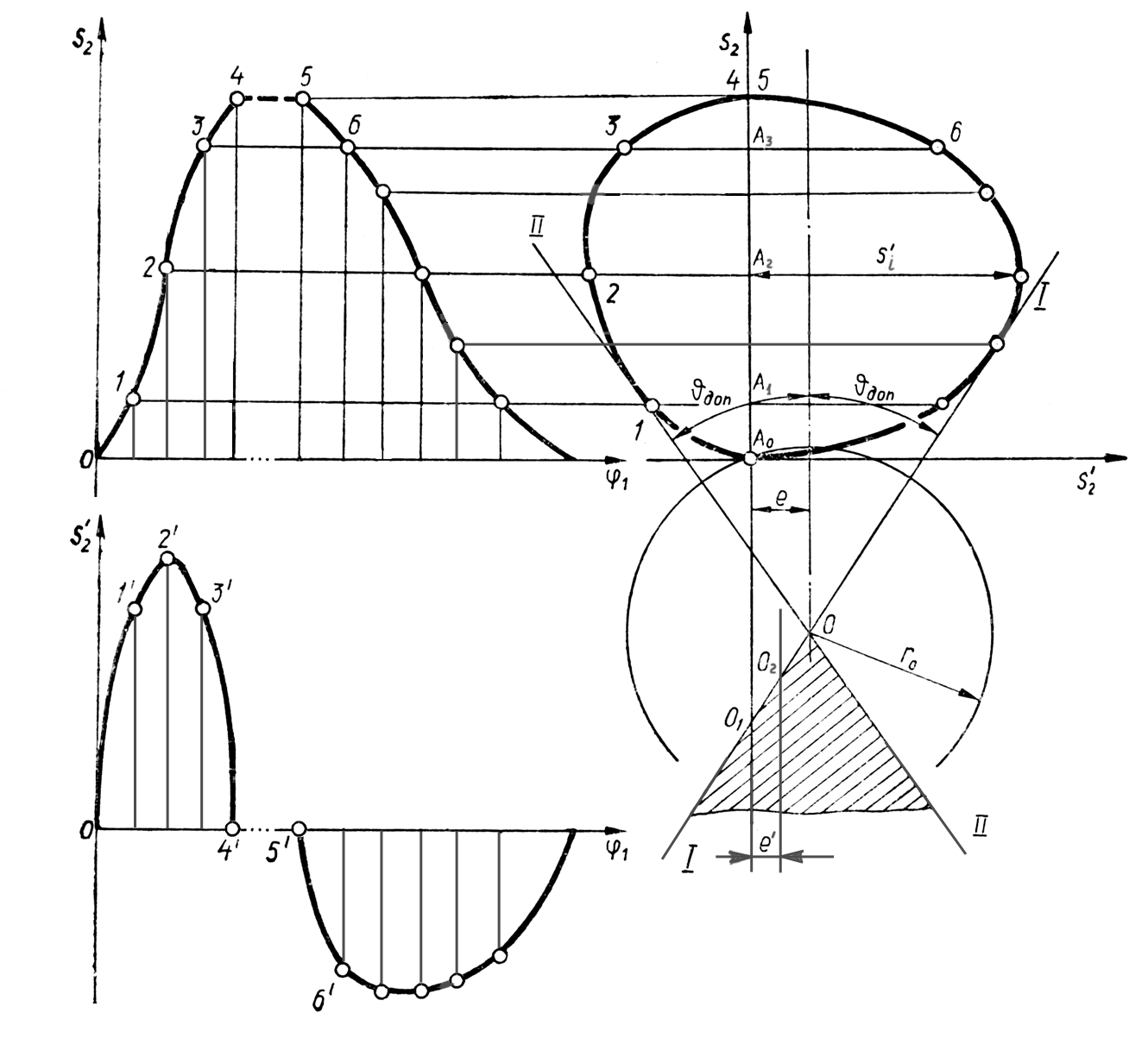
Рис. 8.5

Зауважимо, що в разі жорстких обмежень габаритних розмірів механізму беруть до уваги той факт, що небезпека заклинювання штовхача з силовим замиканням вищої пари має місце лише на фазі віддалення, оскільки при опусканні штовхач рухається під дією пружини (сили тяжіння). У цьому випадку при нереверсивному режимі роботи дотичну І-І проводять через т. А₀. У кулачкових механізмах з геометричним замиканням вищої кінематичної пари умова повинна виконуватись як на фазі віддалення, так і опускання.

Така геометрична інтерпретація співвідношення (8.1) використовується і для графічного визначення габаритних розмірів кулачкових механізмів з коромислом.

Визначення мінімального радіуса кулачка за умовою опуклості профілю. Для кулачкових механізмів із плоским штовхачем при будь-якому положенні кулачка кут тиску є сталим. Зокрема, якщо тарілка перпендикулярна до осі штовхача (найрозповсюдженіший випадок), кут тиску дорівнює нулю. Отже, при проектуванні таких механізмів кут тиску не може бути покладений в основу визначення . У такому випадку ставлять додаткову вимогу: профіль кулачка має бути опуклим. Лише при виконанні цієї умови кожна точка профілю зможе торкнутися тарілки штовхача.

Профіль кулачка буде опуклим, якщо радіус кривини профілю в будь-якій точці буде більшим за нуль, . Цю умову можна виразити нерівністю

. (8.2)

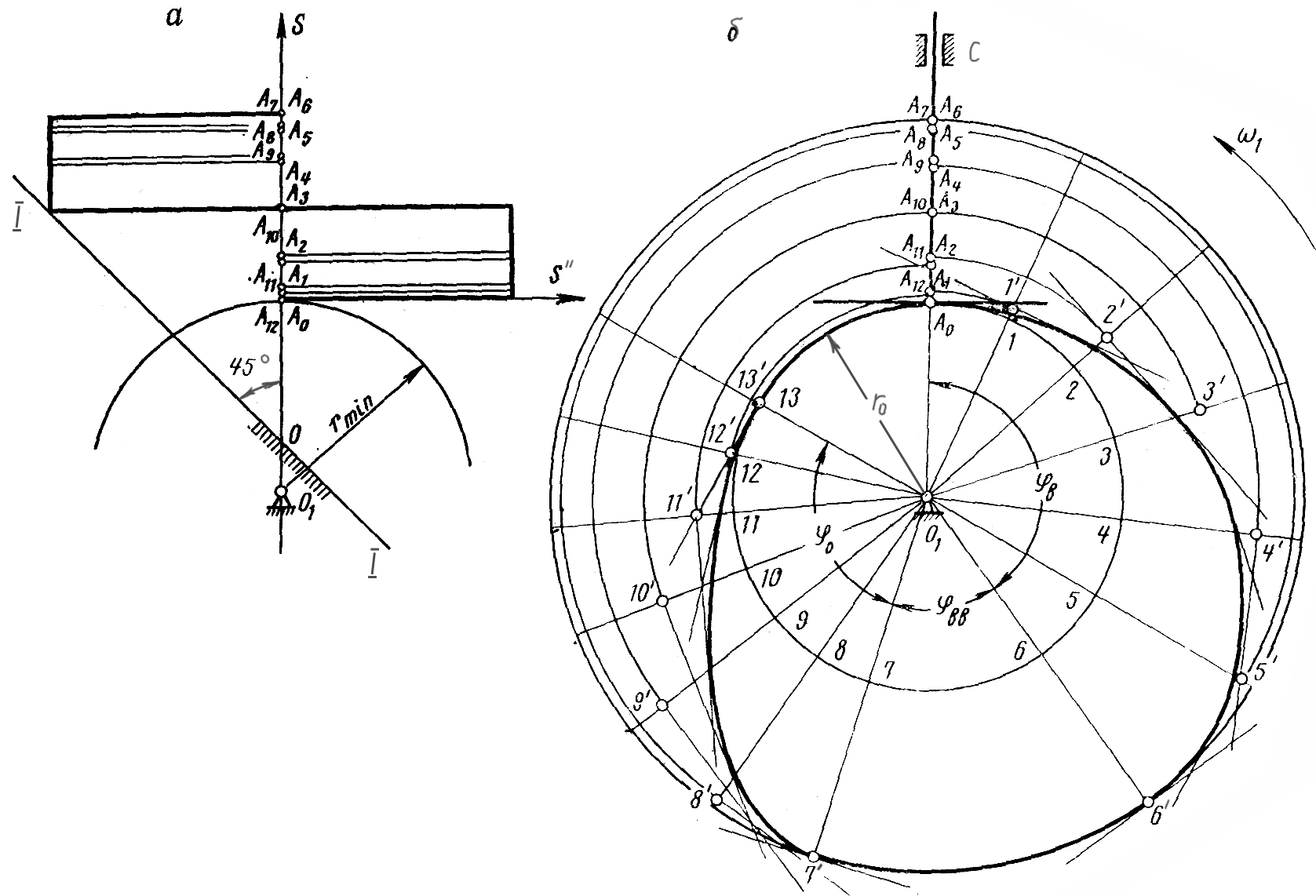
Рис. 8.6

Нерівність (8.2) дозволяє графічно визначити величину , метод проф. Геронімуса. Для цього, на основі попередньо побудованих графіків будується графік . По осі ординат відкладемо значення , а через отримані точки паралельно осі абсцис - відповідні значення (рис. 8.6, а). Уся побудова виконується в одному масштабі . Сполучивши плавною кривою отримані точки, одержимо діаграму

До цієї діаграми, на ділянці, що відповідає максимальному від’ємному значенню під кутом 45⁰ до осі ординат проводиться дотична I-I. Згідно з нерівністю (8.2), за центр обертання кулачка може бути вибрана будь-яка точка, що розміщена нижче за точку перетину дотичної з віссю ординат. Наприклад, на рис. 8.6, а точка О₁, тоді мінімальний радіус є відрізок А₀О₁, а його величина визначається за формулою .

Зауважимо, що в кулачкових механізмах з плоским штовхачем застосування ексцентриситету є недоцільним, оскільки призводить до збільшення габаритів механізмів.