3.2. Загальна методика силового розрахунку

С

а)

иловий аналіз механізмів ґрунтується на розв’язанні першої задачі динаміки – за заданим законом руху визначити діючі сили. Визначення реакцій, а також – у низці задач – сил та моментів, що прикладені до механізму ззовні, складає зміст його силового розрахунку.

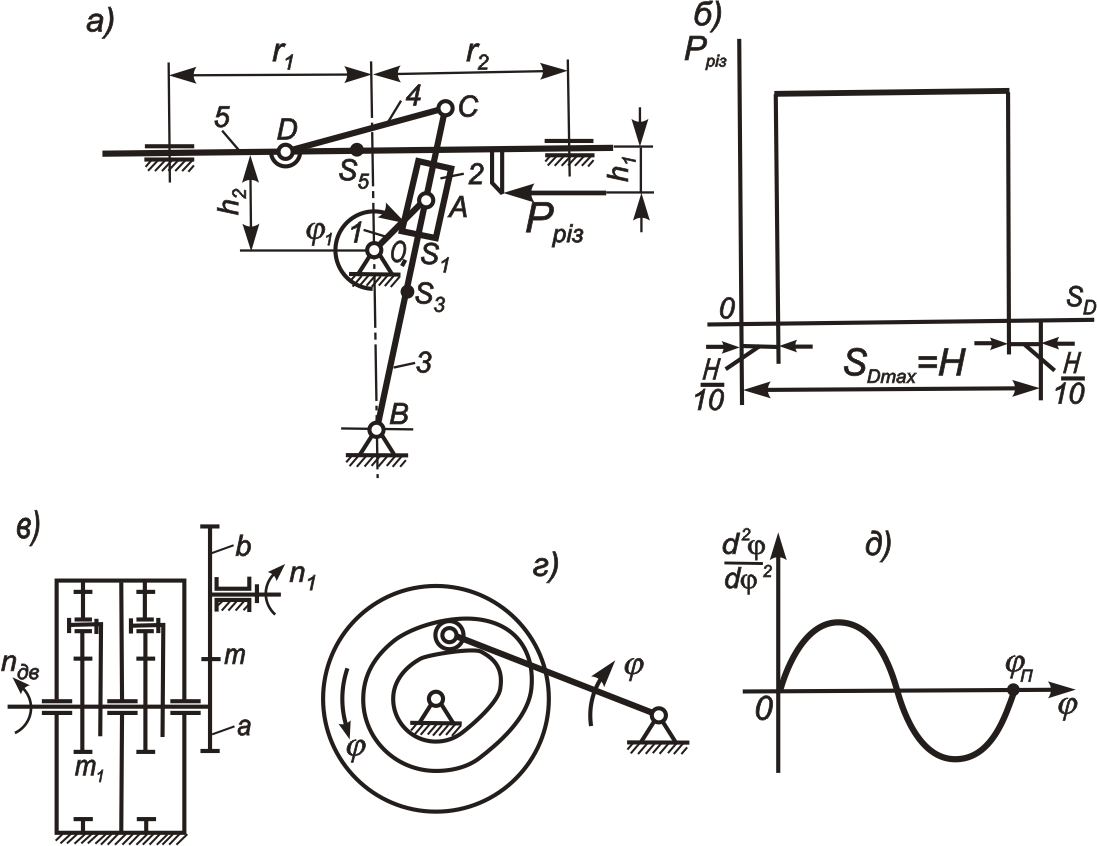
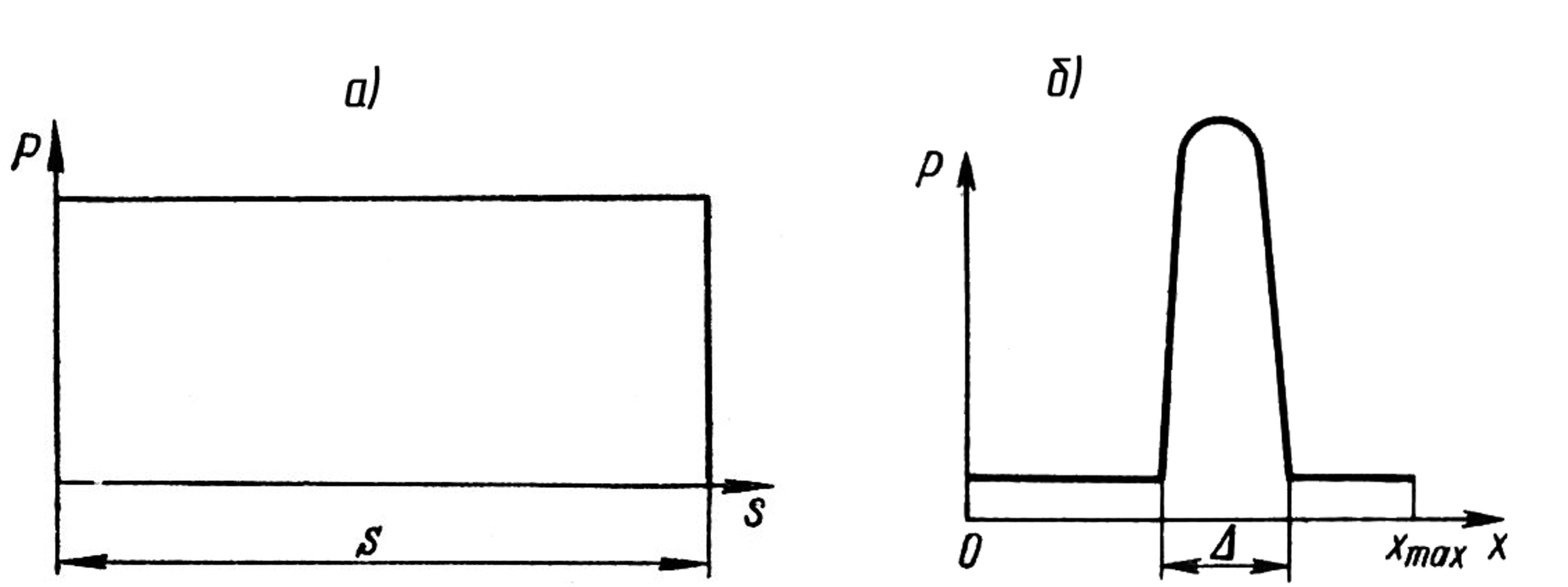
Рис. 3.4

Під час руху механізму в кінематичних парах діють сили, що є силами взаємодії між ланками. Сили взаємодії ланок, що виникають в місцях їх дотику, називають реакціями в кінематичних парах. Навантаженість кінематичних пар реакціями є важливою динамічною характеристикою механізму. Знання сил в кінематичних парах має велике практичне значення для розрахунків ланок механізму на міцність, жорсткість, вібростійкість, стійкість проти спрацьовування, для розрахунку вальниць на довговічність та для проведення інших подібних розрахунків, що виконуються при проектуванні механізмів. Таким чином силовий розрахунок включає, перш за все, визначення реакцій у кінематичних парах. Зовнішні сили, що прикладені до ланок механізму, як правило, задані. Визначенню підлягає лише зовнішня зрівноважувальна сила (зрівноважувальний момент), що прикладена до вхідної ланки, при якій забезпечується прийнятий закон її руху.

Силовий розрахунок механізмів може бути виконаний різними методами. В ТММ досить широке застосування отримав метод силового розрахунку механізмів на основі звичайних рівнянь рівноваги твердих тіл. Суть методу зводиться до застосування рівнянь рівноваги у формі Д’Аламбера. Для цього силу інерції, яка є протидією тіла, що прискорюється, та яка прикладена до тіла, що надає це прискорення, умовно переносять на тіло, що прискорюється. Перенесена сила зрівноважується з усіма зовнішніми силами, в тому числі і з реакціями, що діють на це тіло.

Стосовно механізмів суть методу може бути сформульована так: якщо до всіх зовнішніх сил, що діють на ланку (групу Ассура, механізм) додати сили інерції (моменти), то під дією усіх цих сил ланку (групу Ассура, механізм ) можна розглядати як таку, що умовно перебуває в рівновазі. Цей метод дозволяє записати рівняння руху у формі рівнянь рівноваги, тим самим задачу динаміки розв’язати методами статики.

Таким чином, при застосуванні принципу Д’Аламбера до розрахунку механізмів, крім зовнішніх сил, вводяться в розрахунок сили інерції, які виникають при русі ланок і діють як додаткові (фіктивні) сили. Нагадаємо, під силою інерції розуміють кінетичну реакцію тіла на прискорення, яке надається йому ззовні. Сили інерції – це сили, обумовлені масою та рухом тіла з прискоренням. Сили інерції тіла (ланки) являють собою результат сумарної дії елементарних сил інерції кожної точкової маси тіла. Для зручності розрахунків незлічену систему елементарних сил інерції, що відповідають точковим масам, замінюють рівнодійними силами та парами. В загальному випадку, якщо тіло (ланка) здійснює плоскопаралельний рух, частіше за все елементарні сили інерції зводяться до одного головного вектора сил інерції (скорочено сили інерції), прикладеного в центрі мас тіла, та головного момента сил інерції (скорочено момента сил інерції) , де m – маса тіла; a_s – прискорення центра мас тіла; – кутове прискорення тіла; I_s – момент інерції тіла відносно осі, що проходить через центр мас, перпендикулярно площині його руху. Головний вектор сил інерції спрямований протилежно вектору прискорення центра мас . Головний момент сил інерції спрямований протилежно кутовому прискоренню .

Метод силового розрахунку механізму з врахуванням сил інерції та застосуванням рівнянь динамічної рівноваги часто називають кінетостатичним розрахунком механізмів, на відміну від статичного розрахунку, при якому не враховуються сили інерції. У сучасних швидкохідних машинах слід обов’язково враховувати сили інерції ланок механізму, бо значення цих сил можуть значно перевищувати за величиною прикладене зовнішнє навантаження.

Таким чином, силовий розрахунок механізмів будемо виконувати методом кінетостатики, умовно приклавши до кожної рухомої ланки механізму, крім зовнішніх сил (моментів ), головний вектор та головний момент сил інерції. Тоді для кожної ланки можна записати три рівняння кінетостатики. Нагадаємо, для рівноваги довільної плоскої системи тіл необхідно і достатньо, щоб сума проекцій усіх сил на кожну з двох координатних осей і сума їх моментів відносно будь-якого центра, що лежить у площині дії сил, були рівні нулю.

, (1)

, (2)

. (3)

Часто в розрахунках рівняння (1) та (2) замінюють одним еквівалентним векторним рівнянням

. (4)

Головний вектор та головний момент сил інерції визначаються з відомих формул:

Невідомі реакції визначаються з рівнянь (1) – (4), в які вони входять у складі сум , з відомими зовнішніми силами.

Зазначимо, до викладена методика – для силового розрахунку плоских механізмів. При цьому прийнято, що механізм має площину симетрії, яка паралельна площині руху і в якій діють усі прикладені сили. Вказаній умові відповідає дуже велика кількість механізмів енергетичних, технологічних, транспортних машин та різних приладів.

При русі механізму в його кінематичній парі виникають сили тертя, що гальмують рух, знижують коефіцієнт корисної дії механізму. Силовий розрахунок може бути виконаний як з урахуванням, так і без урахування тертя. У першому наближенні проводять розрахунок без урахування сил тертя в кінематичних парах, розглядаючи механізм як систему з ідеальними в’язями. Відзначимо, у більшості випадків сили тертя малі, порівняно з іншими силами, що діють на механізм, тому уточнений розрахунок часто не робиться.

Розглянемо дію сил в кінематичних парах. Реакція, тобто сила взаємодії ланок, що утворюють нижчу кінематичну пару, представляє собою рівнодіючу елементарних сил (елементарних тисків однієї ланки на іншу), розподілених по поверхні дотику ланок. Як відомо, сила взаємодії між двома тілами, що дотикаються (якщо нехтувати силами тертя), напрямлена по спільній нормалі до поверхні стикання. Таким чином, у поступальній кінематичній парі всі елементарні сили, а отже і їх рівнодійна – реакція R₁₂ (рис. 3.5), будуть напрямлені по нормалі до напрямної кінематичної пари х-х. Реакція, як і будь-яка сила, характеризується трьома параметрами: величиною (модулем), напрямком і точкою прикладання. Величина і точка прикладання реакції невідомі і повинні бути визначені в процесі силового розрахунку. Таким чином, поступальна пара вносить в рівняння (1) – (4) два невідомих параметри. Сказане повністю стосується і реакції R₂₁, яка прикладена до ланки 2 з боку ланки 1, оскільки сили взаємодії ланок R₁₂, R₂₁ зв’язані третім законом Ньютона: Відзначимо, що реакції в кінематичних парах будемо позначати двома нижніми індексами: перший вказує номер ланки, на яку діє сила, другий – номер ланки, з боку якої діє сила.

Розглянемо обертальну кінематичну пару V класу (рис. 3.6). Якщо знехтувати силами тертя, то рівнодійна R₁₂ елементарних тисків однієї ланки на іншу, напрямлена по нормалі до циліндричних поверхонь дотику обох ланок, пройде через центр шарніра O. Положення центра шарніра завжди відоме, але невідомі ні величина цієї реакції, ні її напрям.

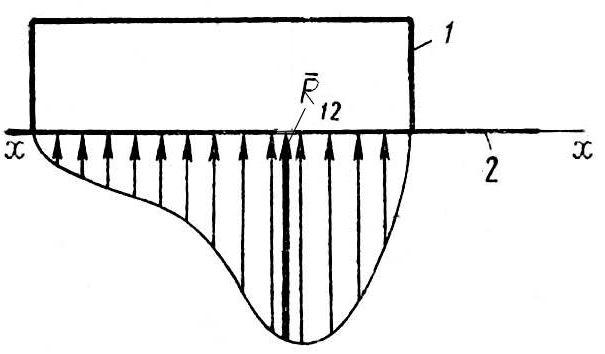
Рис. 3.5

Таким чином, від кожної реакції, що діє в нижчій кінематичній парі, в розрахункових рівняннях (1) – (4) з’являться два невідомі параметри.

У вищій парі IV класу (рис. 3.7) реакція R₁₂ прикладена в точці А дотику ланок 1 та 2 і напрямлена вздовж спільної нормалі n-n (тертя не враховується). Таким чином, для реакції R₁₂ відомі як точка прикладання, так і лінія дії; невідомим є тільки її модуль.

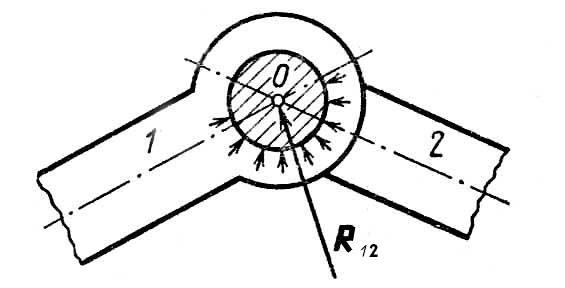
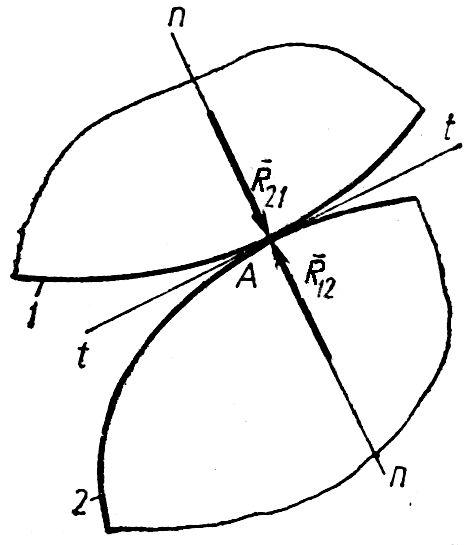
Рис. 3.6 Рис. 3.7

Умови статичної визначеності плоских механізмів, кінематичних ланцюгів. Розглянемо плоский механізм, що складається з n рухомих ланок та p₅ нижчих (V класу) і у p₄ вищих (IV класу) кінематичних пар. Для цього механізму можна скласти 3n рівнянь рівноваги; число невідомих параметрів під час визначення реакцій у кінематичних парах цього ланцюга становитиме 2p₅+p₄. Щоб задача була статично визначеною, кількість рівнянь рівноваги повинна дорівнювати числу невідомих, що входить до них, тобто 3n=2p₅+p₄. Запишемо для плоского кінематичного ланцюга формулу Чебишева у вигляді 3n=2p₅+p₄+W. Порівнюючи вирази, роблять висновок: механізм без залишкових в’язей є статично визначеним. W рівнянь, що залишились, використовуються для визначення тих зовнішніх силових факторів, які не задані в силовому розрахунку і є шуканими. В багатьох підручниках невідомий зовнішній силовий фактор називається зрівноважувальною силою (моментом).

У той же час, для будь-якої структурної групи Ассура справедливе співвідношення 3n=2p₅+p₄. Отже, будь-яка структурна група є статично визначеною, а тому при силовому розрахунку доцільно розглядати рівновагу окремих структурних груп.

Послідовність силового розрахунку механізмів. При силовому розрахунку невідомими будуть внутрішні сили в кінематичних парах, тобто реакції, та часто зрівноважувальна сила (момент). Щоб визначити їх, механізм треба розкласти на групи Ассура. Оскільки групи Ассура є статично визначеними, механізм розкладається на групи Ассура та механізм І класу. При цьому необхідно, щоб зрівноважувальна сила була прикладена до рухомої ланки механізму І класу. Підкреслимо, що при такому розкладанні механізму, в кожній групі Ассура невідомими будуть тільки реакції. Після того, як силовий розрахунок усіх груп Ассура виконано, механізм І класу також буде статично визначеним.

Підсумуємо: силовий розрахунок механізму потрібно проводити за структурними групами Ассура, починаючи з групи, яка приєднана останньою у процесі утворення механізму, і завершувати розрахунком механізму І класу. Таким чином, послідовність силового розрахунку є зворотньою до послідовності кінематичного дослідження.