Вычисление собственных векторов через главные миноры

det(А-λЕ)=0

Рассмотрим матрицу D= Ее размеры 2nx2n

detD=det(А-λЕ) (по теореме Бине-Коши)

Посчитаем detD по теореме Лапласа. Фиксируем первые n строк. Выбираем J столбцов, где J={}{1,..,n}. Их мы выбираем их верхне-левой единичной матрицы. Осталось выбрать n-k столбцов, отличных от столбцов E, иначе оперделитель такой матрицы равен 0, из верхне-правой единично матрицы. Т.о. мы получим один минор det(E,E), где ={1,..,n}\J. Из матрицы D мы выбираем столбцы с номерами из J и из , но увеличенными на n. С дополнительным минором аналогично.

detD== == 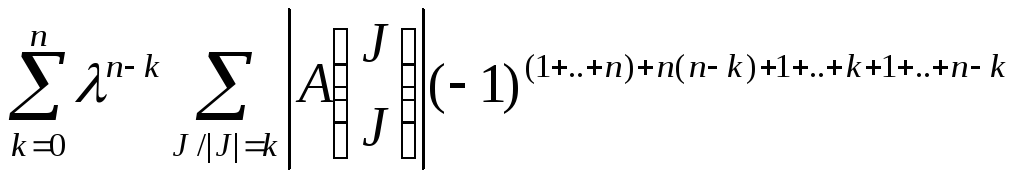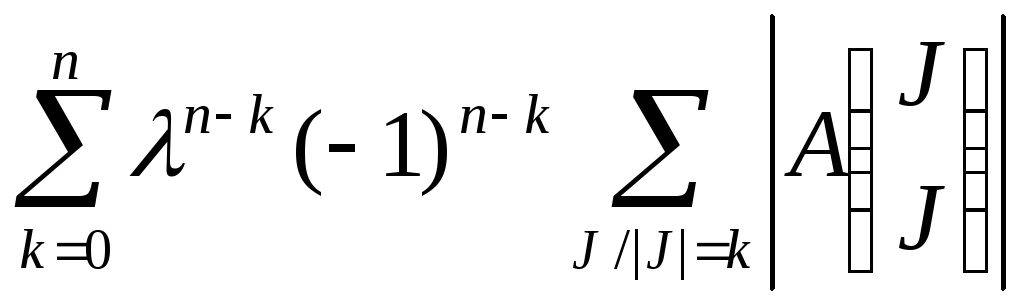Раскласифицировали J по их мощностям.

Определим знак 1+..+n+n(n-k)+1+..+k+1+..+n-k=1/2(n²+n+k²+k+n²-2nk+k²+n-k+2n²-2nk)=2n²+k²-2nk+n≡k²-n≡n-k

Заметим, что 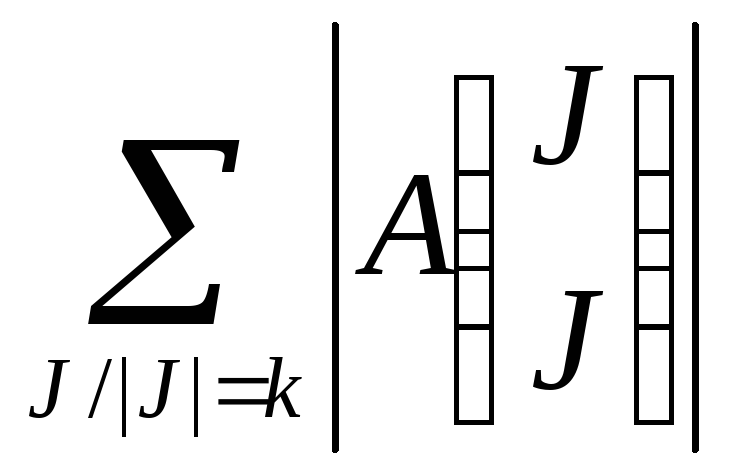=S(A) – сумма главных миноров k-ого порядка матрицы А.

Т.о. |A-λE|=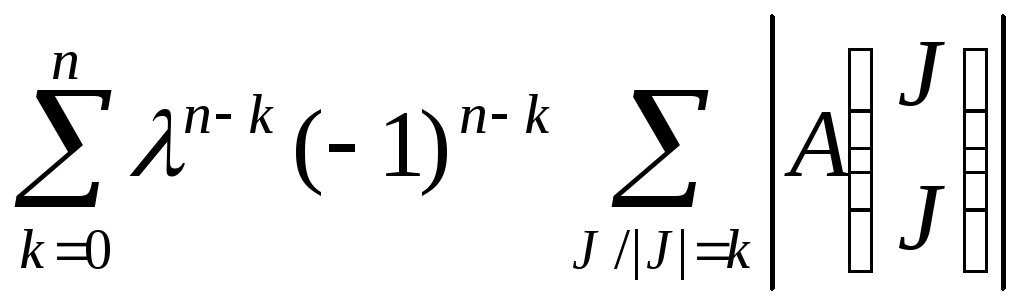

Следствие. Если матрицы А и В подобны, то S(A)=S(B)

Д-во: У подобных матриц характеристические многочлены равны, т.е. равны коээфициентны, т.е. суммы главных миноров.

Пример. Найти характеристический многочлен матрицы Фробениуса.

Рассмотрим характеристический многочлен какого-нибудь преобразования пространства над комплексным полем.

det(А-λЕ)=, где λ- комплексный корень, а n - кратность собственного числа – алгебраическая кратность.

Легко доказать, что множество собственных векторов, соответствующих одному собственному числу, является подпространством

W={x /(А-λЕ)x=0} –подпространство.

dimW=d - геометрическая кратность собственного числа λ

Лемма. У подобных матриц геометрические кратности равны.

Д-во: А подобна В => В=QАQ, где Q – невырожденная. Так как матрицы подобны, то у них равны характеристические многочлены, а соотвественно и собственные числа. Рассмотрим собственное число λ и для него W={x | (A-λE)x=0} и W={x | (B-λE)x=0}. Докажем, что W=W, т.е. множества решений этих уравнений совпадают.

(B-λE)x=(QАQ-λE)x=(QАQ- QλEQ)x=[QEQ=E]= Q(А-λE)Qx=0

Т.о. уравнение (B-λE)x=0 эквивалентно уравнению (А-λE)x=0, т.е. множества их решений совпадают.

Лемма 1. Геометрическая кратность не превосходит алгебраической кратности.

Д-во: Докажем, что dn

Пусть φ – линейное преобразование, А – его матрица в заданном базисе .

- сосбтвенный базис W. Дополним его до базиса

[φ]= 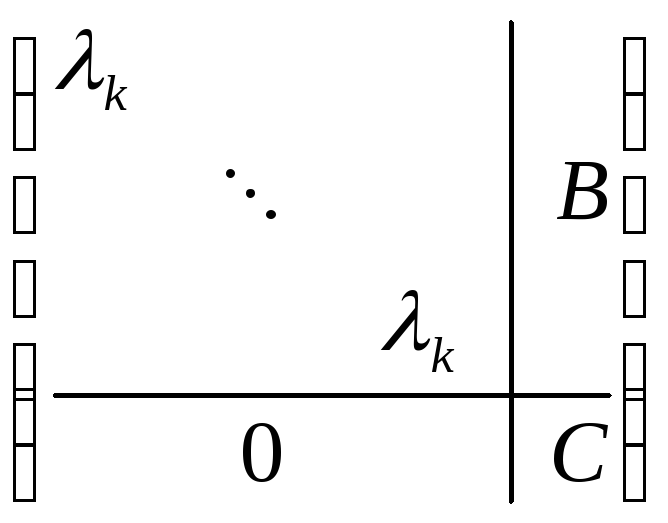φ=λ i=1,..,d [φ]-λE=

det( [φ]-λE)=g(λ) => dn

Лемма 2. Если λ,…,λ -различные собственные числа, то W=Ker(φ- λξ)+..+ Ker(φ- λξ) – прямая сумма.

Д-во: Допустим это не прямая сумма, т.е. x=x+..x и x=y+..y (1)

φy= λy φx=λx k=1,..,m

Проведем индукцию по m. Для m=1: x=x=y верно.

Пусть верно для m-1, докажем истинность для m

(φ- λξ)x=(φ- λξ)x+…+(φ- λξ)x=(λ-λ)x+..+ (λ-λ)x+(λ-λ)x

(φ- λξ)x =(φ- λξ)y+…+(φ- λξ)y=(λ-λ)y+..+ (λ-λ)y

По предположению индукции (λ-λ)x=(λ-λ)y (i=1,..,m-1)

Подставляем в (1), получаем, что x=y

Следствие. Пусть φ в n-мерном пространстве имеет n собственных чисел λ..,λ, тогда существует базис из собственных векторов.

Д-во: Рассмотрим прямую сумму W=Ker(φ- λξ) +..+ Ker(φ- λξ). Имеем n подпространств, сумма размерностей которых равна n. Тогда это одномерные подпространства, причем они инвариантные относительно φ. Пусть e - базисный вектор Ker(φ- λξ) => по определению 2 e - собственный вектор и т.д. Получили систему базисных собственных векторов e,..,е. Она и будет базисом.

Критерий диагонализируемости.

φ диагонализируемо (т.е. существует базис из собственных векторов) тогда и только тогда, когда d+..d=n

Д-во: 1) Пусть существует базис из собственных векторов

Тогда матрица линейного преобразования будет иметь вид

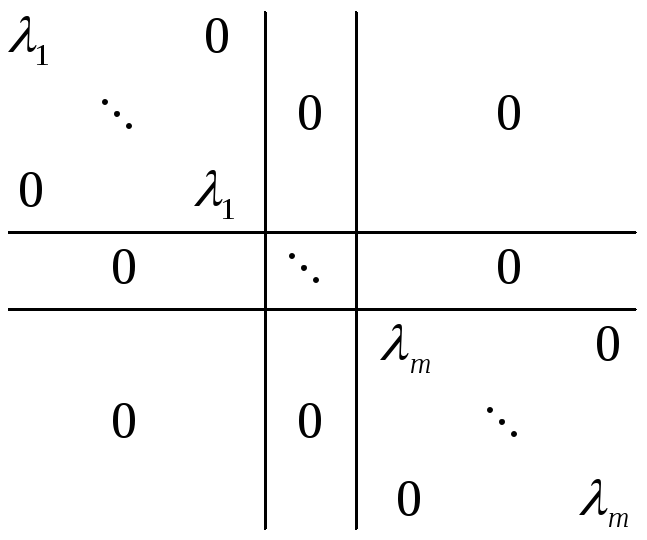Значит d+..d=n.

2) Построим базис Ker(φ- λξ): k=1,..,m

Полученная система векторов будет линейно независимой по лемме 2 (сумма прямая). А так как d+..d=n, то ее можно взять в качестве базиса пространства V. Т.о. мы получили базис из собственных векторов, т.е. матрица имеет диагональный вид.

Следствие 1. (для любого поля) Если существует такое k, что d<n, то φ не диагонализируемо.

Д-во: d+..d<n+..nn, т.е. φ не диагонализируемо.

Следствие 2. Если поле комплексное, то d=n (k=1,..,m) тогда и только тогда, когда φ диагонализируемо.

Д-во: => d+..d= n+..n=n (т.к. поле комплексное)

<= Если существует k, что d<n, то по следствию 1 φ не диагонализируемо, чего быть не может.