
- •7.050102 “Программное обеспечение автоматизированных систем”,
- •7.080407 “Компьютерный эколого-экономический мониторинг ”)
- •Донецк - 2009
- •Рекурсивные функции
- •Теоретическая справка
- •Примитивно-рекурсивные функции
- •Задание на лабораторную работу
- •Контрольные вопросы
- •Машины тьюринга
- •Теоретическая справка Символьные конструкции
- •Определение машины Тьюринга (мт)
- •Задание на лабораторную работу
- •Контрольные вопросы
- •Композиция машин тьюринга
- •Теоретическая справка
- •1. Последовательная композиция машин Тьюринга
- •2. Параллельная композиция машин Тьюринга
- •3. Разветвление или условный переход в композиции машин Тьюринга
- •Задание на лабораторную работу
- •Контрольные вопросы
- •Нормальные алгоритмы маркова
- •Теоретическая справка
- •Функционирование нам
- •Задание на лабораторную работу
- •Контрольные вопросы
- •Перечень рекомендованной литературы
- •7.050102 “Программное обеспечение автоматизированных систем”,
- •7.080407 “Компьютерный эколого-экономический мониторинг ”
Задание на лабораторную работу
-
Составить нормальный алгоритм Маркова над алфавитом А.
-
На конкретных примерах исходных слов продемонстрировать работу составленных алгоритмов.
Варианты заданий
1.
Реализовать алгоритм, выполняющий
замену в слове
![]() в алфавите
в алфавите
![]() каждого символа
каждого символа
![]() на символ
на символ
![]() .
.
2.
Реализовать алгоритм, выполняющий
перестановку в слове
![]() в алфавите
в алфавите
![]() букв таким образом, чтобы сначала стояли
все нули, а затем все единицы.
букв таким образом, чтобы сначала стояли
все нули, а затем все единицы.
3.
Составить нормальный алгоритм,
преобразующий исходную строку в алфавите
![]() в строку, в которой буквы расположены
в алфавитном порядке.
в строку, в которой буквы расположены
в алфавитном порядке.
4.
Реализовать алгоритм, выполняющий
![]() над числами в унарном коде.
над числами в унарном коде.
5.
Реализовать алгоритм, выполняющий
![]() над числами в унарном коде.
над числами в унарном коде.
6.
Реализовать алгоритм, выполняющий
![]() над числами в унарном коде.
над числами в унарном коде.
7.
Реализовать алгоритм, вычисляющий
арифметическое вычитание
![]() в унарном коде.
в унарном коде.
8.
Реализовать функцию выбор аргумента
![]() над числами в унарном коде.
над числами в унарном коде.
9. Реализовать вычисление предиката X=Y в унарном коде с сохранением (восстановлением) исходных данных.
10. Реализовать вычисление предиката X>Y в унарном коде с сохранением (восстановлением) исходных данных.
11.
Реализовать алгоритм в алфавите
![]() ,
меняющий местами первую и последнюю
буквы слова.
,
меняющий местами первую и последнюю
буквы слова.
12.
Реализовать алгоритм над алфавитом
![]() ,
меняющий местами первый ноль и последнюю
единицу.
,
меняющий местами первый ноль и последнюю
единицу.
13.
Реализовать операцию копирование в
алфавите
![]() ,
то есть получить из слова
,
то есть получить из слова
![]() слово
слово
![]() .
.
14.
Реализовать алгоритм над алфавитом
![]() ,
который выдает единицу, если в исходном
слове только парные нули и ноль в
противном случае.
,
который выдает единицу, если в исходном
слове только парные нули и ноль в
противном случае.
15.
Реализовать алгоритм в алфавите
![]() ,
который переставляет буквы в слове
,
который переставляет буквы в слове
![]() так, чтобы сначала шли все нули, потом
– единицы.
так, чтобы сначала шли все нули, потом
– единицы.
16.
Реализовать алгоритм над алфавитом
![]() ,
исключающий в слове последнюю звездочку.
,
исключающий в слове последнюю звездочку.
17. Реализовать алгоритм, реализующий функцию циклический сдвиг двоичного числа на одну ячейку.
18.
Реализовать алгоритм в алфавите
![]() ,
анализирующий последовательность цифр
в слове и выдающий «+», если цифры образуют
неубывающую последовательность, и «–»
в противном случае.
,
анализирующий последовательность цифр
в слове и выдающий «+», если цифры образуют
неубывающую последовательность, и «–»
в противном случае.
19.
Реализовать алгоритм над алфавитом
![]() ,
который выдает 1, если исходное слово
содержит комбинацию baccd,
и 0 - в противном случае.
,
который выдает 1, если исходное слово
содержит комбинацию baccd,
и 0 - в противном случае.
20.
Реализовать алгоритм, выполняющий
следующие действия. В слове
![]() в алфавите
в алфавите
![]() стереть все, кроме
стереть все, кроме
![]() .
Если такой последовательности нет, все
стереть.
.
Если такой последовательности нет, все
стереть.
21.
Реализовать алгоритм над алфавитом
![]() ,
переставляющий буквы в обратном порядке.
,
переставляющий буквы в обратном порядке.
22.
Реализовать алгоритм над алфавитом
![]() ,
который выдает 1, если в исходном слове
содержатся только парные нули, и 0 - в
противном случае.
,
который выдает 1, если в исходном слове
содержатся только парные нули, и 0 - в
противном случае.
23.
Реализовать алгоритм над алфавитом
![]() ,
который выдает «да»,
если в исходном слове четное количество
y-ков,
и «нет» в противном случае.
,
который выдает «да»,
если в исходном слове четное количество
y-ков,
и «нет» в противном случае.
24.
Реализовать алгоритм над алфавитом
![]() ,
выдающий в результате столько единиц,
сколько нулей в исходном слове.
,
выдающий в результате столько единиц,
сколько нулей в исходном слове.
25.
Реализовать алгоритм над алфавитом
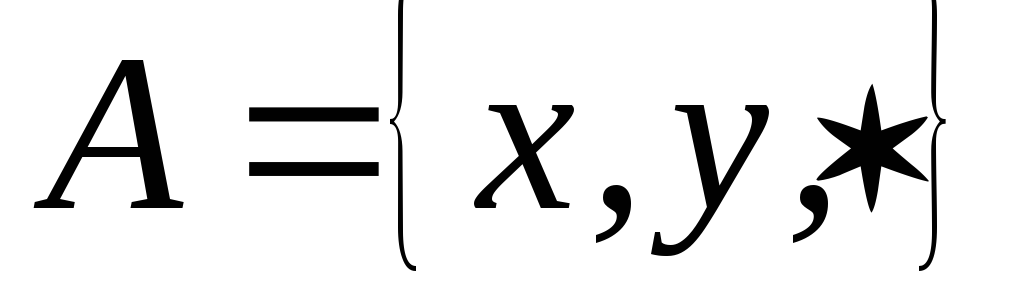 ,
выделяющий часть слова расположенную
между первой парой звездочек.
,
выделяющий часть слова расположенную
между первой парой звездочек.
Контрольные вопросы
-
Что такое Марковская подстановка?
-
Что такое заключительная Марковская подстановка, как она обозначается?
-
В каком случае Марковская подстановка считается неприменимой к некоторому слову?
-
Как функционирует нормальный алгоритм Маркова?
-
В каких случаях НАМ заканчивает работу и останавливается?
-
Чем отличается НАМ в алфавите А от алгоритма над алфавитом А?
-
Привести пример бесконечно работающего нормального алгоритма Маркова.
-
Привести определение нормально вычислимой словарной функции.
-
Сформулировать принцип нормализации.
