2. Определение произведения чисел произвольного ряда

Дан: ряд произвольных чисел .

Определить: произведение этих чисел

Блок-схема вычислительного процесса приведена на рис.2.

Этот алгоритм подобен предыдущему. Отличием является только то, что вычисление произведения осуществляется по рекуррентной формуле , а очистка ячейки памяти, выделенной под переменную , осуществляется не нулем, а единицей по понятным причинам.

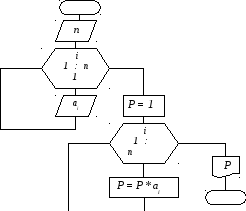
Рис. 2 Блок – схема вычисления произведения ряда чисел

3. Алгоритм определения наибольшего (наименьшего) числа

из заданного ряда чисел

Дан: ряд произвольных чисел .

Определить: наибольшее число a_max и его место в ряде k.

Типовой алгоритм для решения таких задач приведен на рис.3.

Он основан на использовании циклической операции, в которой поочередно производится сравнение всех чисел ряда с числом , играющим роль эталона для сравнения. В качестве начального значения выбирается первый элемент ряда независимо от его истинного значения (наибольшее, наименьшее среди чисел ряда или какое-либо другое).

_

+

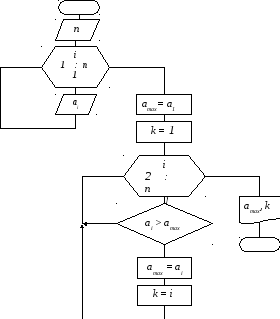
Рис. 3 Блок – схема определения наибольшего числа ряда

Переменная предназначена для хранения текущего адреса максимального числа, на старте этот адрес – единица. Параметр цикла , как и в предыдущих алгоритмах, определяет адрес (порядковый номер) числа ряда и имеет начальное значение 2, так, как первое число уже использовано в роли a_max. Далее выполняется сравнение значения текущего числа ряда , имеющего адрес , с числом, выполняющим на данный момент роль максимального a_max. Если в результате сравнения текущее число окажется большим максимального , то с этого момента роль максимального будет выполнять текущее число a_i, а его адрес будет зафиксирован в качестве значения переменной . Если же результат сравнения будет иным, то никакие изменения не происходят, а сразу выполняется продвижение цикла, то есть устанавливается адрес i следующего числа ряда и производится переход к новому выполнению тела цикла. В результате перебора всех чисел ряда, определяется наибольшее число , его адрес , и их значения выводятся на экран.

Определение наименьшего числа осуществляется аналогично. Для этого в представленном алгоритме (рис.3) идентификатор следует заменить (поскольку этот идентификатор будет отвечать назначению алгоритма) и операцию сравнения заменить операцией .

4. Алгоритм определения наибольшего (наименьшего) значения вычисляемой функции

Дана: функция , область изменения аргумента : от (начальное значение), до (конечное значение), с шагом h.

Определить: наибольшее значение вычисляемой функции _max на заданном интервале и значение аргумента _max, при котором функция принимает максимальное значение.

А

лгоритм решения этой задачи (рис.4) аналогичен алгоритму, приведенному на рис.3. Отличие состоит в том, что в предыдущей задаче значения чисел ряда уже были известны, а в этой их необходимо предварительно вычислять.

В

заголовке цикла, в отличие от предыдущего алгоритма, в качестве параметра цикла используется не адрес числа , а значение аргумента . Параметр цикла изменяется не от начального значения, а от значения , поскольку значение уже было использовано в операции вычисления начального значения функции y_max= f(x_н). Переменная x_max хранит текущее значение аргумента, при котором функция принимала максимальное значение. После завершения работы цикла значение переменной будет равно максимальному значению функции на заданном интервале при значении аргумента x = x_max.

О

пределение наименьшего значения вычисляемой функции производится аналогично. Для этого, в приведенной на рис.4 блок – схеме, идентификаторы необходимо заменить , x_max на x_min, а операцию сравнения – на операцию .

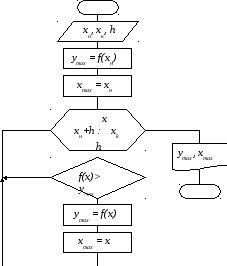
Рис. 4. Блок – схема вычисления наибольшего значения функции.