Глава 3. Ряды и интеграл Фурье

§1. Ортогональные системы функций

Рассмотрим множество кусочно-непрерывных функций заданных на отрезке При этом в точках разрыва значением функции будем считать полусумму пределов слева и справа. Скалярное произведение двух функций этого множества определим следующим интегралом

(1)

Можно убедиться, что интеграл (1) удовлетворяет всем аксиомам скалярного произведения. Поэтому множество кусочно-непрерывных функций является евклидовым пространством. Обозначим его

Евклидово пространство, как известно, является одновременно метрическим и нормированным. Норма и метрика, согласованные со скалярным произведением, определяются формулами

(2)

Определение 1. Последовательность элементов евклидова пространства называется ортонормированной, если где символ Кронекера.

В качестве примера ортонормированной последовательности (системы) функций рассмотрим последовательность тригонометрических функций, определенных на отрезке

(3)

Убедимся, что последовательность (3) ортонормированная. Обозначим

(Четный индекс отвечает косинусам, нечетный - синусам).

Тогда

Итак, первый член последовательности (3) ортогонален всем последующим.

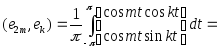
Аналогично найдем

Итак, мы убедились, что последовательность (3) является ортонормированной на отрезке

Пусть на интервале определена непрерывная функция такая, что

(4)

где ( называется весовой функцией).

Число, определяемое формулой

(5)

для любых двух функций называют скалярным произведением этих функций с весом

Если то функции называются ортогональными с весом. Примером системы функций, ортогональных с весом, является система многочленов Чебышева

(6)

Убедимся, что система (6) ортогональна на отрезке с весовой функцией

Действительно,

(7)

Из (7) видно, что многочлены Чебышева (6) ортогональны с весом, причем

Можно доказать, что система функций Бесселя где к-й корень уравнения ортогональная на отрезке с весом причем (8)

Кроме приведенных выше существует множество других ортогональных систем функций, например, многочлены Лежандра, Лагерра, Якоби и др.

Упражнение. Доказать, что последовательность тригонометрических функций ортогональна на отрезке Нормировать эту последовательность.

§2. Ряд Фурье, свойства

В евклидовом n-мерном пространстве существует, как известно, ортонормированный базис и всякий вектор x этого пространства разлагается по этому базису

(1)

Коэффициенты разложения (координаты вектора x в этом базисе) определяются формулой

(2)

В бесконечномерном функциональном евклидовом пространстве роль базиса играет ортонормированная последовательность функций, а конечная сумма (1) превращается в функциональный ряд.

Определение 1. Пусть функция и ортонормированная система функций принадлежат евклидову пространству. Ряд

(3)

называется рядом Фурье функции если его коэффициенты определяются формулой

(4)

Здесь знак соответствия ~ вместо знака равенства стоит потому, что не известно, сходится ли ряд Фурье, и если сходится, то к какой функции.

Пусть частичная сумма ряда Фурье, а частичная сумма другого ряда по той же ортонормированной системе, но с другими коэффициентами. Величину называют отклонением частичной суммы от функции

Теорема 1. Наименьшее отклонение от функции имеет частичная сумма ряда Фурье.

Доказательство. Найдем

Итак,

(5)

Поскольку в (5) все величины неотрицательные, то ясно, что квадрат отклонения будет наименьшим при т.е. при Теорема доказана.

Поскольку то из (5) при получим

(6)

(7)

Из (7) видно, что частичные суммы числового ряда с неотрицательными членами ограничены. Такой ряд сходится (см. §2 гл.5, ч.1). По необходимому признаку сходимости ряда имеем при Таким образом, мы доказали первое следствие.

Следствие 1. Коэффициенты ряда Фурье стремятся к нулю при

Поскольку ряд сходится, то переходя к пределу в (7), получим

(8)

Неравенство (8) называется неравенством Бесселя. Из (6) получим

(9)

Равенство (9) доказывает второе следствие.

Следствие 2. Необходимым и достаточным условием сходимости ряда Фурье функции к этой функции по метрике (норме), согласованной со скалярным произведением, является равенство Парсеваля

(10)

Определение 2. Ортонормированная система функций называется полной в евклидовом пространстве, если ряд Фурье по этой системе любой функции этого евклидового пространства сходится к данной функции по норме, согласованной со скалярным произведением.

Если ортонормированная система полная, то разложение в ряд Фурье по этой системе единственное. Отметим без доказательства, что приведенные в предыдущем параграфе ортонормированные системы функций являются полными в А это означает, что любую кусочно-непрерывную функцию можно разложить по этим системам функций в ряд Фурье, который будет сходиться к этой функции по норме (2) §1. Такая сходимость, как известно, называется средней квадратичной. Понимая сходимость в таком смысле, впредь будем писать знак равенства вместо знака соответствия ~.

Замечание. На практике часто разлагают в ряд Фурье не по ортонормированной системе функций а по ортогональной, но не нормированной

(11)

Коэффициенты Фурье находятся по формуле

(12)

Пример 1. Разложить функцию

по системе многочленов Чебышева

Решение.

Итак, (13)

Пример 2. Разложить функцию

по системе функций Бесселя

Решение. Согласно (12)

Воспользовались табличным интегралом