2.2. Сопротивление r, индуктивность l, емкость c в цепях постоянного и синусоидального тока.

Цель работы:

Исследовать особенность работы элементов R, L, C в цепях постоянного и синусоидального тока. Построить волновые и векторные диаграммы токов и напряжений на данных элементах.

Общие теоретические положения

Взаимосвязь между токами и напряжениями на идеализированных элементах R, L, C определяется следующими соотношениями:

, , ,

где , , -мгновенные значения напряжений на элементах, , ;

– мгновенное значение тока.

В зависимости от временного закона изменения исходных функций токов и напряжений указанные соотношения могут давать различные результаты. Покажем это на примере цепей синусоидального и постоянного тока.

1. Цепь синусоидального тока

При подключении активного сопротивления R к источнику синусоидального тока, мгновенное значение которого , напряжение на нем будет изменяться по закону:

,

где – амплитудное значение тока;

 - круговая частота синусоидального тока.

Сопоставление функций u и i показывает, что они изменяются в фазе с одинаковой частотой.

Активная мощность P, выделившаяся на R в виде тепла, может быть определена по формуле:

P = U I = I² R,

где U, I – действующие значения (измеряются приборами).

При подключении к источнику синусоидального тока, мгновенное значение которого i = I_msin t катушки индуктивности, обладающей активным сопротивлением R_k, мгновенное напряжение на ее зажимах будет равно сумме напряжений u_rk и u_L в соответствии со 2-м законом Кирхгофа:

u = u_RK + u_L = I R + L di/dt = R_k I_m sin t + L I_m cos t,

где I_m – амплитудное значение тока;

L – индуктивность катушки;

L – ее индуктивное сопротивление.

Полученный результат говорит о том, что напряжение u_L опережает ток i, текущий через катушку, на угол /2, изменяясь с той же угловой частотой .

Модуль полного комплексного сопротивления катушки выразится:

.

Между напряжением на катушке u и током через нее i возникает фазовый сдвиг, который можно найти из треугольника сопротивлений

.

Активная мощность будет выделяться на активном сопротивлении R_k:

P_к = U I cos_,,

где U, I – действующие значения напряжения на катушке и тока через нее.

При подключении к источнику синусоидального напряжения, мгновенное значение которого u = U_m sint, конденсатора, токами утечки которого можно пренебречь, ток через него определяется по формуле:

,

где 1/С – емкостное сопротивление конденсатора;

U_m – амплитудное значение подводимого напряжения.

Ток через конденсатор i изменяется с той же угловой частотой , что и подводимое напряжение u, но опережает его при этом на угол +/2 (или напряжение отстает от тока на угол -/2).

Пренебрегая токами утечки через диэлектрик конденсатора, можно говорить о том, что он не потребляет активной мощности из источника, т.е. P = 0.

2. Цепь постоянного тока

При подключении тех же элементов R, L, C в цепь постоянного тока ( = 0) картина распределения токов и напряжений в них претерпевает изменения.

Для активного сопротивления R эта взаимосвязь по -прежнему определяется законом Ома:

U = I R,

где U и I – постоянные напряжение и ток.

Мощность P, выделяющаяся на сопротивлении R в виде тепла, будет:

P = U I = I² R.

Для индуктивной катушки можно записать, что Z = R_к т.к. ее индуктивное сопротивление на постоянном токе L = 0. Напряжение на ней в этом случае примет вид:

U = I R_к,

а потребляемая активная мощность P = U_к I = I² R_к – аналогична мощности, выделяемой на обычном резисторе.

Емкостное сопротивление конденсатора в цепи постоянного тока равно бесконечности и ток через него не протекает, а значит и мощность P = 0.

План работы:

1. Произвести сборку каждой из трех схем, изображенных на рис2.2.1 с параметрами, указанными в табл. 2.2.1 и подключить к источнику синусоидального напряжения.

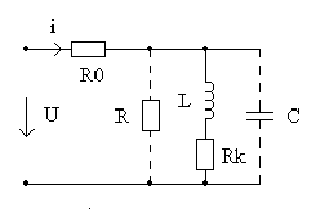
Рис. 2.2.1. Схемы для исследования разнородных элементов.

Таблица 2.2.1

Параметры № варианта	U, B	R, Oм	L, мГн	Rк, Oм	С, мкф	R0, Oм	f, кГц
1	4	200	20	-	0,47	100	1
2	4	300	20	-	0,33	400	3
3	4	100	5	-	0,1	200	5
4	4	400	5	-	0,1	100	7

1. Провести измерение тока в каждой из трех схем и внести в табл.2.2.2.

2. По результатам измерений рассчитать P, Q, S, cos_{к ,}cosφ .

4. Провести измерение тока в этих схемах при постоянном источнике напряжения.