3. Основы молекулярной физики и термодинамики

Конденсированное состояние. Кинематика и динамика жидкостей. Основные понятия, определения и законы молекулярной физики и термодинамики. Статистический метод исследования. Основы термодинамики. Реальные газы. Фазовые равновесия и превращения. Кинетические явления.

3.1. Примеры решения задач

1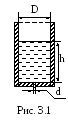. В дне цилиндрического сосуда диаметром D=0,5 м имеется круглое отверстие диаметром d=1 см. Найти зависимость скорости понижения уровня воды в сосуде от высоты h этого уровня. Найти значение этой скорости для высоты h=0,2 м (рис. 3.1).

Решение. Обозначим: S₁ – площадь поперечного сечения сосуда и v₁ – скорость течения воды в нем (скорость понижения уровня воды в сосуде), S₂ – площадь поперечного сечения отверстия и v₂ – скорость вытекания воды из отверстия.

По теореме Бернулли

или ,

откуда

,

где  – плотность воды;

g – ускорение силы тяжести;

h – высота уровня жидкости.

Используя теорему о неразрывности струи v₁S₁=v₂S₂, можно определить v₂:

v₂=v₁S₁/S₂.

Подставляя v₂ в формулу v₁, будем иметь:

v₁²=(v₁S₁/S₂)²-2gh.

Решая полученное уравнение относительно v₁, получим

Учитывая, что S₁=D²/4 и S₂=d²/4, имеем

Так как d⁴<<D⁴, то приближенно, скорость понижения уровня воды в сосуде в зависимости от высоты h этого уровня, определяется соотношением

Отметим, что если d=D, то

Подставляя значения величин входящих в полученную формулу в единицах СИ, произведя вычисление, окончательно будем иметь

v₁=0,8 мм/с=0,810^-3 м/с.

Ответ: v₁=0,810^-3 м/с.

2. Цилиндрический бак высотой h=1 м наполнен до краев водой. За какое время t вся вода выльется через отверстие, расположенное у дна бака, если площадь S₂ поперечного сечения отверстия в 400 раз меньше площади поперечного сечения бака? Сравнить это время с тем, за которое понадобилось бы для вытекания такого же объема воды, если бы уровень воды в баке поддерживался постоянным на высоте h=1 м от отверстия (рис. 3.2).

Решение. Для определения скорости понижения уровня воды в баке воспользуемся уравнением Бернулли в виде

.

Откуда

,

где  – плотность жидкости;

v₁ – скорость течения воды в баке (скорость понижения уровня воды в баке);

v₂ – скорость вытекания воды из бака;

y – высота уровня воды в баке (переменная величина);

ρ – давление жидкости.

В силу неразрывности струи

,

где S₁ – площадь поперечного сечения бака;

S₂ – площадь поперечного сечения отверстия.

Из уравнения имеем

.

Подставляя значение скорости вытекания воды в выше записанное уравнение, получим

.

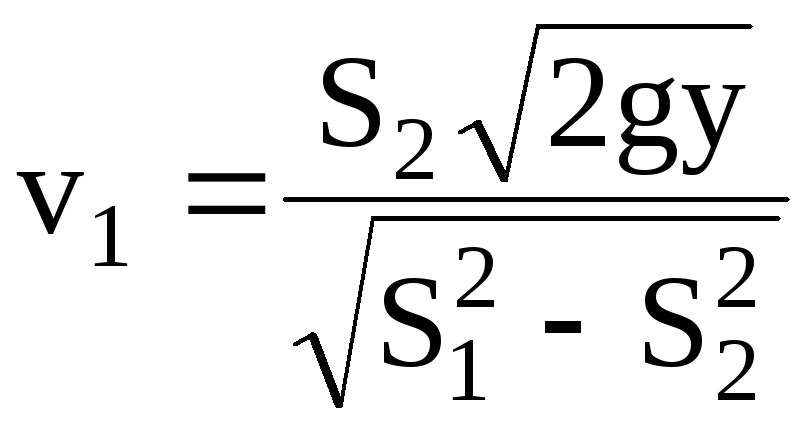За время dt уровень воды в баке понизится на

.

Откуда имеем

.

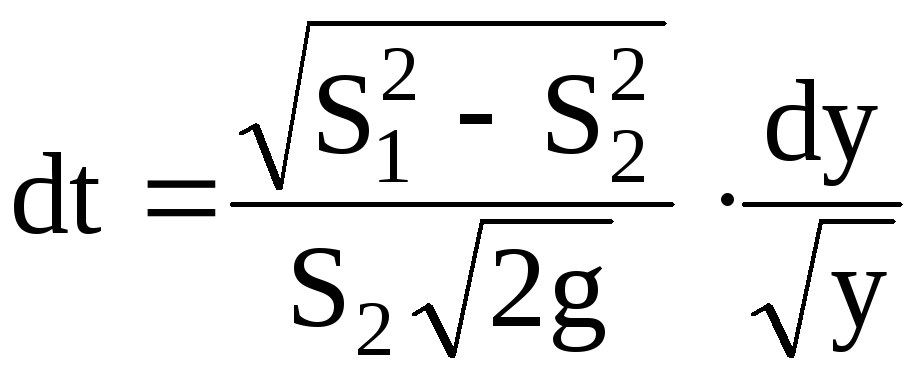Проинтегрировав это выражение, получим

.

Подставив численные значения, произведя вычисления, имеем

с.

Нетрудно убедиться, что если бы уровень воды в баке поддерживался постоянным на высоте h=1 м от отверстия, то время вытекания воды было бы в два раза меньше.

О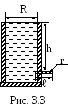твет: t=1,8·10² с.

3. В боковую поверхность цилиндрического сосуда радиусом R=2 см вставлен горизонтальный капилляр, внутренний радиус которого r=1 мм и длина ℓ=2 см. В сосуд налито касторовое масло, динамическая вязкость которого η=1,2 Пас (рис. 3.3). Найти зависимость скорости v понижения уровня касторового масла в сосуде от высоты h этого уровня над капилляром. Найти значение этой скорости при h=26 см.

Решение. Скорость понижения уровня касторового масла в сосуде зависит от скорости протекания масла через капилляр.

Объем масла, протекающего за время t через капилляр, определяется формулой Пуазейля

V=r⁴tp/(8ℓ),

где r – радиус капилляра;

p – изменение давления на концах капилляра;

ℓ – длина капилляра;

 – динамическая вязкость жидкости (касторового масла).

Разность давлений на концах капиллярах обусловлена гидростатическим давлением слоя жидкости, т.е.

p=gh.

С другой стороны,

V=S'v't=r²v't,

где v' – скорость протекания масла через капилляр.

Решая совместно вышенаписанные уравнения относительно v, получим

v'=r²gh/(8ℓ).

В силу теоремы о неразрывности струи

v₁S₁=v₂S₂ ,

где v – скорость понижения уровня масла в сосуде;

S – площадь поперечного сечения сосуда.

Окончательно для скорости понижения уровня масла в сосуде, будем иметь

v=r⁴gh/8ℓR².

Подставляя значения величин входящих в полученную формулу в единицах СИ, произведя вычисление, окончательно будем иметь

v=(110^-3)⁴0,9610³9,80,26/8210^-21,22²=310^-5 м/с.

Ответ: v=310^-5 м/с.

4. К пружинным весам подвешена тонкая металлическая пластина. Нижний ее край длиной L=10,0 см приведен в соприкосновение с поверхностью жидкости, которая полностью смачивает пластину. После этого пластину начинают медленно поднимать. Перед ее отрывом от жидкости поверхность последней принимает сложную форму, изображенную на рисунке 3.4. При этом свободная поверхность жидкости у границы с пластиной располагается приблизительно в вертикальной плоскости. Зная, что для отрыва пластины потребовалась сила F=0,4510^-3 кгс, определить коэффициент поверхностного натяжения жидкости.

Решение. Чтобы найти коэффициент поверхностного натяжения, нужно, как это следует из формулы б=F/ℓ, необходимо знать силу поверхностного натяжения, действующую на единицу длины какого–либо контура, ограничивающего поверхность жидкости. Таким контуром является линия соприкосновения свободной поверхности жидкости с пластиной, имеющей форму очень узкого прямоугольника. Следовательно, ее длина равна 2L (длиной двух других сторон пренебрегаем).

На пластину вдоль каждой единицы длины этого контура действует со стороны жидкости сила поверхностного натяжения, равная коэффициенту поверхностного натяжения. Векторы этих сил перпендикулярны контуру и являются касательными к свободной поверхности жидкости. Поэтому в условиях данной задачи они направлены вертикально вниз и, следовательно, параллельны друг другу. Поэтому результирующая сила поверхностного натяжения F_н, действующая на пластину, также направлена вертикально вниз и равна сумме сил, действующих на отдельные элементы контура, т.е.

F=2Lσ.

Для отрыва пластины от жидкости необходимо приложить силу F, направленную вертикально вверх, которая бы уравновесила силу поверхностного натяжения. Следовательно,

F_н=F=2Lσ.

Откуда

σ=F/2L.

Выразим входящие в формулу величины в единицах СИ: L=0,100 м, F=4,410^-3 Н. Выполнив вычисление, найдем

σ=4,410^-3/20,100=2210^-3 Н/м.

Примечание. Существенно, что в данной задаче пластина была тонкой, так что площадью ее соприкосновения с жидкостью, площадью прямоугольника, можно было пренебречь. В противном случае необходимо учитывать отрицательное давление, создаваемое в жидкости около пластины вследствие кривизны ее поверхности. Тогда соотношение F_н=F оказывается неверным. Кроме того, для толстой пластины силы поверхностного натяжения, приложенные к отдельным элементам прямоугольного контура, не будут даже приблизительно параллельны друг другу и поэтому соотношение F_н=2Lσ также перестанет выполняться. Решение задачи в случае толстой пластины становится сложным.

Ответ: σ=2210^-3 Н/м.

5. Какую работу против сил поверхностного натяжения надо совершить, чтобы выдуть мыльный пузырь радиусом 0,05 м? Чему равно избыточное давление внутри пузыря (рис. 3.5)?

Решение. Мыльный пузырь представляет собой очень тонкую мыльную пленку мыльной воды приблизительно сферической формы. Эта пленка имеет две поверхности – наружную и внутреннюю. Пренебрегая толщиной пленки и считая, поэтому радиусы сфер одинаковыми, их общая площадь будет равна

S=8R².

Поскольку до образования пузыря поверхность мыльной воды, из которой он выдут, была весьма мала, можно считать, что записанное соотношение выражает изменение (увеличение) площади поверхности мыльной воды на S.

Увеличение поверхности жидкости на S связано с увеличениием поверхностной энергии

W=σS.

Совершаемая при выдувании пузыря работа против сил поверхностного натяжения идет на увеличение поверхностной энергии

A=W=8R²σ.

Для определения избыточного давления внутри пузыря учтем, что каждая из двух сферических поверхностей пузыря (наружная и внутренняя) производит вследствие своей кривизны давление на воздух внутри пузыря. Это давление, производимое каждой сферой, можно найти по формуле Лапласа, имея в виду, что радиусы кривизны всех нормальных сечений для сферы равны ее радиусу, следовательно, R₁=R₂=R. Таким образом, избыточное давление воздуха внутри пузыря

p=2p_пов=4σ/R.

Взяв из таблицы значение для мыльной воды (σ=4010^-3 Н/м) и выполнив вычисление, получим

A=W=83,14(0,05)²4010^-3=2,510^-3 Дж.

p=44010^-3/0,05=3,2 Па.

Ответ: A=2,510^-3 Дж=2,5 мДж; p=3,2 Па.

6. Вертикально расположенная капиллярная трубка длиной ℓ=200 мм с запаянным верхним концом своим нижним концом приведена в соприкосновение с поверхностью воды. На какую высоту поднимется вода в трубке, если ее радиус R₀=2,010^-4 м? Атмосферное давление p=1,0010⁵ Па. Считать, что вода полностью смачивает трубку.

Решение. Здесь нельзя применять формулу:

h=2σ/rg,

где  – плотность жидкости;

g – ускорение свободногопадения;

σ – коэффициент поверхностного натяжения.

Эта формула определяет высоту поднятия жидкости в капилляре при полном смачивании и справедлива лишь для открытой с обоих концов трубки.

Для решения задачи рассмотрим столбик воды, находящийся в равновесии в капилляре, после того как он уже поднялся под действием сил поверхностного натяжения. Согласно условию равновесия разность давлений у его концов равна гидростатическому давлению, производимому столбиком жидкости высотой h на его основание, т.е.

p₁-p₂=gh,

где p₁ и p₂ – давления внизу и вверху столба соответственно.

Так как жидкость у нижнего края трубки находится в состоянии равновесия, то давление внизу столба (точка 1 на рисунке 3.6) равно давлению в воде у ее открытой поверхности, т.е. атмосферному давлению

p₀=p₁,

Поскольку столб воды ограничен сверху изогнутой поверхностью, давление p₂ вверху (точка 2) отличается от давления p_в воздуха в трубке на величину p_пов, следовательно

p₂=p_в+p_пов.

При расчете давления p_пов учтем, что мениск в узком капилляре имеет форму полусферы и, следовательно, R₁=R₂=R . Поэтому

p_пов=2б/R,

где R=R₀.

Так как данный мениск вогнутый, то p_пов<0. Значит, следует считать R=-R₀. Тогда

p_пов=-2б/R₀,

Давление воздуха в трубке можно выразить через данные величины p₀, ℓ, h при помощи закона Бойля-Мариотта. Воздушный столб высотой (ℓ-h) при давлении p_в имел при атмосферном давлении p_o высоту ℓ. Поскольку объем столба пропорционален его длине, то можно записать:

p_в(ℓ-h)=p₀ℓ; p_в=p₀ℓ/(ℓ-h).

Подставив в формулу разности давлений значения p₁ и p₂ с учетом p_пов, p_в, будем иметь

p₀-(p₀ℓ/(ℓ-h)-2б/R)=gh.

Взяв из таблиц значения ρ и σ для воды, выразив в единицах СИ величины, входящие в последнее соотношение, подставив их и решив квадратное уравнение относительно h, получим

h₁=11 м; h₂=0,014 м.

Поскольку должно выполняться очевидное неравенство h<ℓ, то ответом на вопрос задачи является второе значение.

Ответ: h=0,014 м.

7. На полированную стеклянную пластинку капнули 0,010 г воды и наложили сверху вторую такую же пластинку. Вода растеклась между пластинками по площади круга радиуса R=3,0 см, не дойдя до ее краев. С какой силой надо растягивать обе пластинки, чтобы их разъединить? Считать, что вода полностью смачивает стекло.

Решение. Сначала выясним, почему возникает сила притяжения между пластинками. При наложении пластинок свободная поверхность воды вследствие полного смачивания образует вогнутый мениск в виде полуокружностей (рис. 3.7). Следовательно, давление в жидкости, заключенной между пластинками, меньше атмосферного на величину p_пов, определяемую по формуле

p_пов=σ(1/R₁+1/R₂),

где R₁ и R₂ – радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости. При этом p_пов положительно, если поверхность жидкости выпуклая, и отрицательно, если – вогнутая.

Под избытком внешнего давления пластины сближаются, вода растекается между ними все более тонким слоем. Этот процесс прекратится, когда жидкость дойдет до краев пластин, после чего мениск распрямится, а поверхностное давление и сила притяжения между пластинами исчезнут, или когда дальнейшее сближение пластин станет невозможным из-за того, что они начнут соприкасаться друг с другом в некоторых точках вследствие неровностей их поверхности. Очевидно, что именно последний случай имеет место в задаче.

Сила притяжения между пластинками равна избыточному внешнему давлению p_пов, умноженному на площадь одной пластины, т.е.

F=p_повS=p_пов σR²,

где R – радиус круга растекания жидкости.

Чтобы определить величину p_пов, рассмотрим два взаимно перпендикулярных нормальных сечения поверхности жидкости. Очевидно, радиус кривизны R₁ первого сечения равен половине расстояния между пластинками; радиус кривизны R₂ второго сечения равен радиусу круга растекания жидкости. Поскольку при этом выполняется неравенство R₁<<R₂, то в формуле для избыточного давления, можно пренебречь величиной 1/R₂, т.е. кривизной второго сечения, и рассматривать мениск приближения как вогнутую цилиндрическую поверхность. Таким образом, получим

p_пов=σ/R₁=2σ/d,

где d – расстояние между пластинками, которое можно определить, разделив объем воды на площадь ее растекания:

d=V/S=m/R²,

где m – масса воды;

 – ее плотность.

Наконец определим силу притяжения между пластинками:

F=2²σR⁴/m.

Чтобы разъединить пластинки, их надо растягивать с силой, по крайней мере, равной силе их взаимного притяжения. Таким образом, полученная формула дает ответ на поставленный в задаче вопрос.

Взяв из таблиц значения σ и  для воды, выразим входящие величины в единицах СИ: R=3,010^-2 м, σ=0,073 Н/м, =1,0010³ кг/м³, m=1,010^-5 кг. Произведем вычисление, получим

F=1,210³ Н.

Ответ: F=1,210³ Н=0,12 кН.

8. Найти плотность масла в гидравлической системе пресса при давлении 50010⁵ Па, если плотность его при 20 ^oС и давлении 1,01310⁵ Па равна 910 кг/м³, а коэффициент сжатия равен 610^-10м²/Н.

Решение. По определению, коэффициент сжатия

К=-dV/Vdp,

где dV – изменение объема;

V – первоначальный объем;

dp – изменение давления.

Разделяя переменные имеем

-dV/V=Kdp.

Проинтегрируем это выражение в заданных пределах:

Получаем

Ln(V_к /V_н)=-Kp; или V_к=V_н exp(-Кp)≈V_н(1-Kp).

Так как плотность =m/V, то

m/V_к=m/V_н(1-Kp),

т.е.

_к=_н/(1-Kp).

Подставляя значения величин входящих в полученную формулу в единицах СИ, произведя вычисление, окончательно будем иметь

_к=910/(1-610^-1049910⁵)=938 кг/м³.

Ответ: _к=938 кг/м³.

9. Определить для серной кислоты: 1) относительную молекулярную массу; 2) молярную массу.

Решение. 1. Относительная молекулярная масса вещества равна сумме относительных атомных масс всех элементов, атомы которых входят в состав молекулы данного вещества, и определяется по формуле

,

где n_i – число атомов i-го элемента, входящих в молекулу;

A_ri – относительная атомная масса i-го элемента.

Химическая формула серной кислоты имеет вид H₂SO₄. Так как в состав молекулы серной кислоты входят атомы трех элементов, то стоящая в правой части равенства сумма будет состоять из трех слагаемых и формула примет вид

_r=n₁A_r1+n₂A_r2+n₃A_r3.

Из формулы серной кислоты далее следует, что n₁=2, n₂=1, n₃=4.

Значения относительных атомных масс водорода, серы и кислорода соответственно равны A_r1=1, A_r2=32, A_r3=16. Подставив значения n_i и A_ri, будем иметь

_r=2+32+64=98.

2. Зная относительную молекулярную массу, найдем молярную массу серной кислоты по формуле

 =_rk,

где k=10^-3 кг/моль.

Подставив в последнее выражение значения величин, получим =9810^-3 кг/моль.

Ответ: _r=98; =9810^-3 кг/моль.

10. Определить молярную массу смеси _см кислорода массой m₁=25 г и азота массой m₂=75 г.

Решение. Молярная масса _см смеси, это отношение массы смеси m_см к количеству вещества _см смеси:

_см=m_см/_см.

Масса смеси равна сумме масс компонентов смеси:

m_см=m₁+m₂.

Количество вещества смеси равно сумме количеств вещества компонентов

Подставив выражения m_см и _см в ранее записанную формулу для молярной массы получим

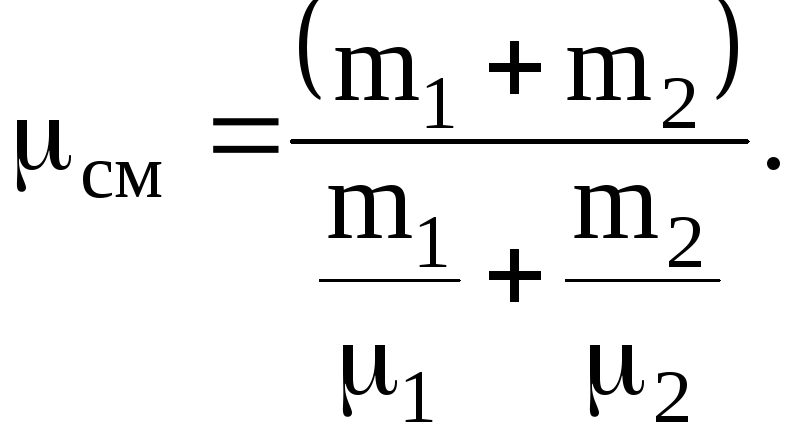
где ₁=3210^-3 кг/моль, ₂=2810^-3 кг/моль.

Подставив значение величин и произведя вычисление, будем иметь _см=28,9.10^-3 кг/моль.

Ответ: _см=28,9·10^-3 кг/моль.

11. Определить число молекул N, содержащихся в объеме V=1 мм³ воды, и массу m₁ одной молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекул.

Решение. Число молекул N, содержащихся в некоторой системе массой m, равно произведению постоянной Авогадро на количество вещества

N=N_А.

Так как =m/, где – молярная масса, то

N=(m/)N_А.

Выразив в формуле массу как произведение  плотности на объем V, получим

N=(V/)N_А.

Произведем вычисления, учитывая =1810^-3 кг/моль,

=110³ кг/м³, V=110^-9 м³, N=6,0210²³ моль^-1.

.

Массу одной молекулы m₁ можно найти по формуле:

Если молекулы воды плотно прилегают друг к другу, то можно считать, что на каждую из них приходится объем (кубическая ячейка)

V₁=d³,

где d – диаметр молекулы.

Тогда

d=V₁^1/3.

Объем V₁ найдем, разделив молярный объем V_m на число молекул в моле, т.е. на N_А:

V₁=V_m /N_А.

Для диаметра одной молекулы будем иметь

d=(V_m/N_А)^1/3,

где V_m=/p.

Окончательно

d=(/(p N_А))^1/3.

Произведем вычисления

м.

Ответ: ; м.

12. В баллоне объемом 10 л находится гелий под давлением p₁=1 МПа и при температуре T=300 К. После того как из баллона было взято m=10 г гелия, температура газа понизилась до Т=290 К. Определить давление гелия оставшегося в баллоне.

Решение. Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, применив его дважды к начальному и конечному состояниям газа:

;

,

где m₁, m₂ – масса гелия в баллоне в начальном и конечном состояниях;

μ – молярная масса гелия;

R – универсальная газовая постоянная;

T₁ и T₂ – температуры газа в начальном и конечном состояниях.

Массы m₁ и m₂ гелия найдем из уравнения Менделеева-Клапейрона:

m₁=p₁V/RT₁,

m₂=μp₂V/RT₂.

Тогда масса гелия оставшегося в баллоне будет равна

Для давления (p) гелия, оставшегося в баллоне, будем иметь:

или

Численно

МПа.

Ответ: p=0,364 МПа.

13. Баллон содержит 80 г кислорода и 320 г аргона. Давление смеси 1МПа, температура 300 К. Принимая данные газы за идеальные, определить объем баллона.

Решение. По закону Дальтона, давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. Парциальные давления кислорода p₁ и аргона p₂ можно определить, воспользовавшись уравнением Менделеева-Клапейрона

p₁=m₁RT/(m₁V);

p₂=m₂RT/(m₂V).

По закону Дальтона, давление смеси газов

или

откуда объем баллона

Подставив численные значения, будем иметь:

10^-3 м³.

Ответ: V=26,210^-3 м³.

14. Какое количество молекул находится в комнате объемом 80 м³ при температуре 17 ^oС и давлении 750 мм. рт. ст.?

Решение. Количество молекул N, содержащееся в комнате, можно определить, зная массу воздуха m,его молярную массу μ и число Авогадро N_А. Число молекул в одном киломоле газа равно числу Авогадро. А число киломолей содержащихся в массе m , определяется соотношением:

=m/.

Следовательно,

N=m/(N_А).

Массу m содержащегося в комнате воздуха определяем из уравнения Менделеева-Клапейрона

,

где p – давление воздуха;

V – объем;

R – универсальная газовая постоянная;

T – абсолютная температура (T=t+273);

m – масса воздуха.

Следовательно, для числа молекул воздуха имеем:

Подставляя все данные, предварительно выразив их в системе СИ, будем иметь

молекул.

Ответ: N=210²⁴ молекул.

15. Найти среднюю кинетическую энергию вращательного движения одной молекулы кислорода при температуре T=350 К, а также кинетическую энергию вращательного движения всех молекул кислорода массой 4 г.

Решение. Согласно теореме о равномерном распределении энергии по степеням свободы, на каждую степень свободы приходится энергия:

,

где k – постоянная Больцмана;

Т – абсолютная температура.

Молекула кислорода двухатомная, поведение такой молекулы описывается 5-ю степенями свободы (три из них приписываются поступательному движению и две – вращательному).

Следовательно, кинетическая энергия вращательного движения молекулы кислорода может быть рассчитана по формуле:

<Wвр>=2<Wк>=2(1/2) kТ=kТ.

Энергия вращательного движения всех молекул, содержащихся в 4 г кислорода, может быть определена как произведение числа молекул N на энергию одной молекулы:

Wк=N<Wвр>=NkТ.

Число молекул определяется соотношением:

где – молекулярная масса кислорода;

m – его масса;

N_А – число Авогадро.

Таким образом:

Подставив численные значения, предварительно выразив их в системе СИ, будем иметь:

<Wвр>=1,3810^–23350=4,8310^–21 Дж.

Дж.

Ответ: W_к=364 Дж.

16. Масса 10 г кислорода находится при давлении 304 кПа и температуре 10 ^oС. После расширения вследствие нагревания при постоянном давлении кислород занял объем 10 л. Найти объем газа до расширения, температуру газа после расширения, плотности газа до и после расширения.

Решение. Согласно условию задачи, расширение газа вследствие нагревания происходило при постоянном давлении. В этом случае оказывается справедливым соотношение

.

Для определения температуры газа после расширения воспользуемся уравнением Менделеева-Клапейрона для конечного состояния газа

,

где p₂ – давление газа после расширения;

V₂ – его объем после расширения;

m – масса газа;

 – молекулярная масса кислорода;

R – универсальная газовая постоянная;

T₂ – абсолютная температура газа.

Следовательно, для конечной температуры имеем

Для определения объема газа до расширения можно вновь воспользоваться уравнением Менделеева-Клапейрона, записанным для первоначального состояния газа:

где p₁, V₁, T₁ – его давление, объем и температура до расширения.

Из данного уравнения имеем

.

Учитывая то, что плотность газа ₁=m/V₁, подставляя значения V₁ и V₂ из уравнений Менделеева-Клапейрона, записанные для соответствующих состояний, для плотности кислорода до и после расширения будем иметь

и

Подставляя численные значения в системе СИ, окончательно имеем

;

л;

₁= 4,14 кг/м³;

₂=1кг/м³.

Ответ: ; л; ₁= 4,14 кг/м³; ₂=1кг/м³.

17. Масса газа 12 г занимает объем 4 л при температуре 7 ^oC После нагревания газа при постоянном давлении его плотность стала равной 0,6 кг/м³. До какой температуры нагрели газ?

Решение. Воспользовавшись уравнением Менделеева-Клапей-рона

можно показать, что между плотностью газа =m/V и давлением существует связь

Следовательно, в начальном состоянии давление газа

В конечном

Так как нагревание газа производилось при постоянном давлении, то p₁=p₂

отсюда

Подставляя численные значения в системе СИ для конечной температуры, будем иметь:

Ответ: T₂=1400 K.

18. В баллоне находилась масса m₁=10 кг газа при давлении p₁=10 МПа. Какую массу газа взяли из баллона, если давление стало равным p₂=2,5 МПа? Температуру газа считать постоянной.

Решение. Запишем уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) для двух состояний: начального и конечного

и

Из второго соотношения определяем объем сосуда и подставляем его значение в первое уравнение, имеем:

а

Из последнего соотношения получаем связь между давлением газа в сосуде и его массой для данного случая:

Отсюда масса газа оставшегося в баллоне:

.

Так как масса израсходованного газа m=m₁–m₂, то окончательно, после соответствующих преобразований, имеем

Подставляя численные значения (в системе СИ) определяем массу взятого из баллона газа:

кг.

Ответ: Δm=7,5 кг.

19. В сосуде находится масса m₁=14 г азота и масса m₂=9 г водорода при температуре 10 ^oС и давлении 1 МПа. Найти молярную массу смеси и объем сосуда.

Решение. По закону Дальтона давление смеси газов равно сумме парциальных давлений компонентов входящих в смесь

p=p₁+p₂,

где p – давление смеси;

p₁ – парциальное давление азота;

p₂ – парциальное давление водорода.

Из уравнения Менделеева-Клапейрона:

Для каждого из давлений (смеси и парциальных) можно записать:

;

;

.

Следовательно, так как p=p₁+p₂, имеем:

.

Откуда

Из последнего соотношения для молекулярной массы смеси будем иметь:

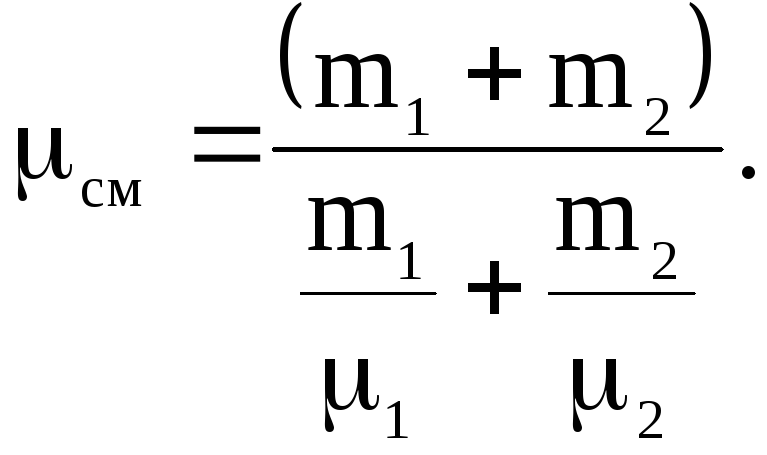
Из уравнения Менделеева-Клапейрона, для смеси газов, объем сосуда равен:

Подставляя численные значения в системе СИ, находим молекулярную массу смеси:

кг/кмоль.

и объем сосуда

м³.

Ответ: μ_см=4,6 кг/кмоль; V=11,710^-3 м³.

20. Для получения хорошего вакуума в стеклянном сосуде, для удаления адсорбированного газа, необходимо прогревать стенки сосуда при откачке. На сколько может повыситься давление в сферическом сосуде радиусом 10 см, если адсорбированные молекулы перейдут со стенок в сосуд? Площадь поперечного сечения молекул S_o=10^–19 м². Температура газа в сосуде 300 ^oС. Слой молекул на стенках считать мономолекулярным.

Решение. Для определения давления воспользуемся основным уравнением молекулярно–кинетической теории в виде

p=n_okT,

где n_o – число молекул в единице объема;

k – постоянная Больцмана;

Т – абсолютная температура газа.

С учетом того, что

n_o=N/V,

где N – число молекул в объеме V, для давления имеем

По условию задачи слой молекул в сосуде мономолекулярный, следовательно, число молекул в нем можно определить исходя из соображений:

,

где S=4r² – площадь поверхности сосуда;

S_o – площадь поперечного сечения молекул газа.

Так как сосуд сферический, то его объем V=4/3r³.

Таким образом, окончательно для давления газа в сосуде будем иметь соотношение:

Подставляя численные значения в полученное соотношение (в системе СИ) определяем давление газа в сосуде

Па.

Ответ: p=2,4 Па.

21. В воздухе содержится 23,6% кислорода и 76,4% азота (по массе) при давлении 100 кПа и температуре 13 ^oС. Найти плотность воздуха и парциальные давления кислорода и азота.

Решение. Для определения плотности воздуха воспользуемся уравнениемМенделеева-Клапейрона

откуда

а

Для определения парциальных давлений так же воспользуемся уравнением Менделеева-Клапейрона, записанным для каждого из компонентов, входящих в смесь воздуха:

где V – объем воздуха.

Откуда

Так как =m/V, то V=m/, следовательно

Подставляя численные значения в системе СИ, для плотности воздуха и парциальных давлений кислорода и азота будем иметь:

кг/м³;

кПа;

кПа.

Ответ: ρ=1,2 кг/м³; p₁=21 кПа; p₂=79 кПа.

22. В сосуде находится количество =10^–7 моль кислорода и масса m₂=10^–6 г азота. Температура смеси 100 ^oС, давление в сосуде p=133 мПа. Найти объем сосуда, парциальные давления кислорода и азота и число молекул в единице объема.

Решение. Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, записанным для смеси газов в виде

,

где _см=₁+₁=(₁+m₂/₂) – число молей или киломолей газов составляющих смесь.

Имеем

pV=(₁+m₂/₂)RT.

Отсюда

V=(₁+m₂/₂)(RT/p).

Парциальные давления компонентов образующих смесь определяем так же из уравнения Менделеева-Клапейрона, записанным для каждого из газов

p₁V=₁RT и p₂V=(m₂/₂)RT.

Откуда для парциальных давлений кислорода и азота соответственно имеем

p₁=₁RT/V и p₂=m₂RT/₂V.

Для определения числа молекул в единице объема необходимо воспользоваться основным уравнением молекулярно – кинетической теории для давления

p=n_okT.

Из него

n_o=p/kT.

Подставляя в ранее полученные формулы ы системе СИ для объема, парциальных давлений кислорода и азота и числа молекул в единице объема, имеем:

м³;

мПа;

мПа;

м^-3.

Ответ: V=3,2·10^-3 м³; p₁=98 мПа; p₂=35 мПа; n=2,6·10¹⁹ м^-3.

23. Один моль идеального 2–х атомного газа, занимает объем 12,3 л под давлением 2 ат. нагревается при постоянном объеме до давления 3 ат. Далее газ расширяется при постоянном давлении до объема 24,6 литра, после чего охлаждается при постоянном объеме до начального давления, и наконец, сжимается при постоянном давлении до начального объема. Определить температуру газа для характерных точек цикла (рис. 3.8).

Решение. Пусть V' – наименьший объем газа;

V" – наибольший объем газа;

p'– наименьшее давление газа;

p" – наибольшее давление газа;

T₁, T₂, T₃, T₄ – температуры газа в характерных точках.

Температуру T₁ можно определить используя уравнение Менделеева-Клапейрона, записанном в виде:

.

Откуда

Переход газа из состояния 1 в состояние 2 – изохорный, для которого справедливо соотношение:

Следовательно,

Переход газа из состояния 2 в состояние 3 – изобарный, для которого справедливо соотношение:

.

Откуда

Переход газа из состояния 3 в состояние 4 – изохорный, для которого справедливо соотношение

следовательно,

Подставляя численные значения из условия задачи, будем иметь:

К;

К;

К;

К.

Ответ: T₁=290 К; T₂=435 К; T₃=870 К; T₄=580 К.

24. Плотность смеси азота и водорода при температуре 47 ^oС и давлении p=2,00 ат равна=0,30 г/л. Найти концентрации молекул азота (n₁) и водорода (n₂) в смеси.

Решение. Концентрацию однородного по составу газа можно найти из формулы

p=n_okT.

В условии задачи дана смесь двух газов, молекулы которых различаются по массе. Приведенная формула является следствием основного уравнения кинетической теории газов

p=(2/3)n_o<W_к>,

где n_o – число молекул в единице объема (концентрация молекул);

<W_к>=<mv²>/2 – средняя кинетическая энергия поступательного движения одной молекулы газа. Для однородных по составу частиц газа <W_к>=mv²/2.

Из основного уравнения кинетической теории газов вытекает, что оно справедливо для совокупности любых частиц, в том числе различных по массе. Следовательно, формулу p=n_okT можно применять для смеси газов. В этом случае n_o – полное число частиц в единице объема. Таким образом, имеем

n_o=p/kT.

Для определения концентрации азота и водорода кроме очевидного соотношения

n₁+n₂=n_o=p/kT

необходимо иметь еще одно уравнение, связывающее величины n₁ и n₂.

Используя данные задачи, можно найти молярную массу смеси рассматриваемых газов (m_см), пользуясь уравнением Менделеева-Клапейрона

pV=mRT/_см или p=RT/_см.

Откуда

_см=RT/p.

С другой стороны, можно выразить _см через молярные массы азота (₁) и водорода (₂), а также их концентрации n₁ и n₂, записав уравнение газового состояния для каждого из газов входящих в смесь

pV=mRT/_см, p₁V=m₁RT/₁, p₂V=m₂RT/₂.

Откуда

p=mRT/(_cмV), p₁=m₁RT/(₁V), p₂=m₂RT/(₂V).

На основании закона Дальтона, давление смеси газов равно сумме парциальных давлений

p=p₁+p₂.

Имеем

p=m₁RT/ ₁V+m₂RT/₂V=(m₁/₁+m₂/₂)RT/V,

где (m₁/₁+m₂/₂)=(m₁+m₂)/_см.

Для молярной массы смеси азота и водорода получаем

_см=₁₂(m₁+m₂)/(₁m₂+₂m₁).

Заметим также, что между массой m газа и его концентрацией n существует связь:

m=nVm'=nV/N_А,

где V – объем газа;

 – его молярная масса;

m' – масса одной молекулы;

N_А – число Авогадро.

С учетом последнего соотношения, для молярной массы смеси имеем:

_см=(₁n₁+₂n₂)/(n₁+n₂).

Решив систему уравнений, найдем неизвестные n₁ и n₂:

n₁=(RT-p₂)/(kT(₁-₂)), n₂₌(RT-p₁)/(kT(₂-₁)).

Выражая входящие в формулы величины в единицах СИ, подставив их значения, выполнив вычисления, получим

n₁=3,5710²⁴ м^-3; n₂=4,110²⁵ м^-3.

Ответ: n₁=3,5710²⁴ м^-3; n₂=4,110²⁵ м^-3.

25. Средняя квадратичная скорость молекул некоторого газа 450 м/с. Давление газа 50 кПа. Найти плотность газа при этих условиях.

Решение. Средняя квадратичная скорость молекул газа связана с его температурой соотношением

,

где R – универсальная газовая постоянная;

μ – молекулярная масса газа;

T – абсолютная температура газа.

Для определения температуры газа воспользуемся уравнением Менделеева-Клапейрона

,

где =m/V – плотность газа.

Следовательно,

.

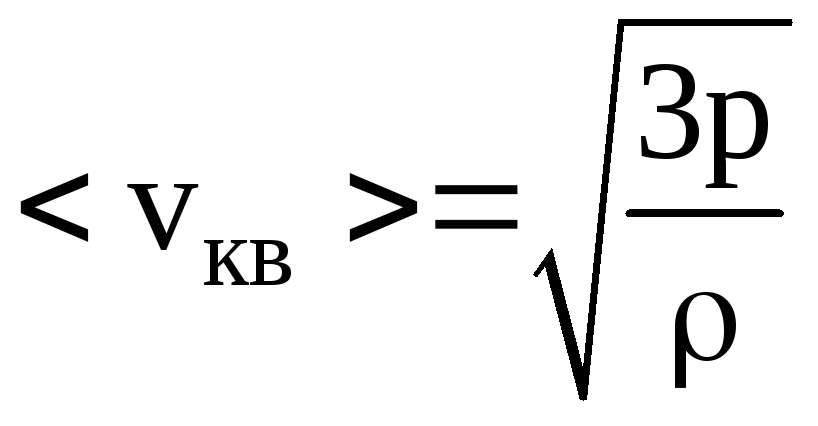Откуда

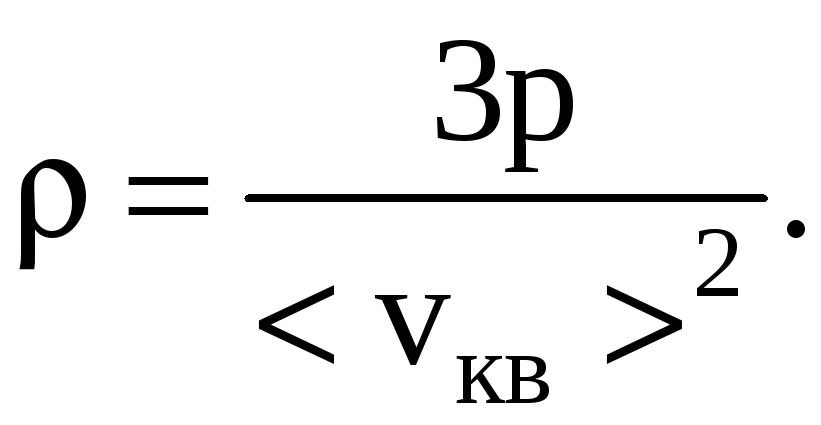
Подставляя численные значения, имеем:

кг/м³.

Ответ: ρ=0,74 кг/м³.

26. Найти среднюю длину свободного пробега молекул воздуха при нормальных условиях. Эффективный диаметр молекул воздуха =0,3 нм.

Решение. Средняя длина свободного пробега молекул газа

,

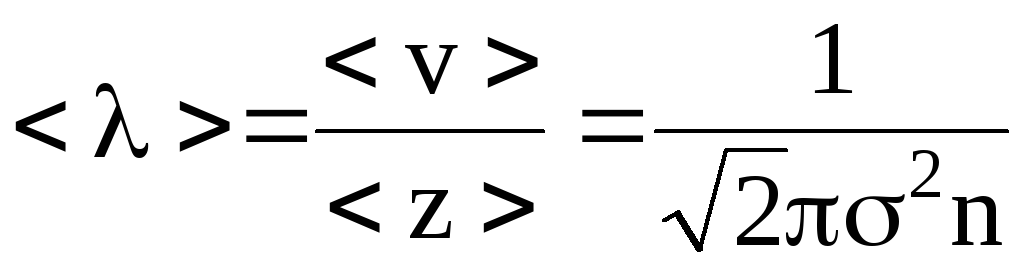где <v> – средняя арифметическая скорость молекул;

<z> – среднее число столкновений каждой молекулы с остальными молекулами в единицу времени;

σ – эффективный диаметр молекулы;

n – число молекул в единице объема (концентрация молекул). Для определения числа молекул в единице объема воспользуемся основным уравнением молекулярно–кинетической теории для давления

p=nkT,

,

где k – постоянная Больцмана;

Т – температура газа.

Тогда для средней длины свободного пробега имеем

.

Подставляя численные значения, окончательно получаем:

=9310^-9 м=93 нм.

Ответ: <λ>=93 нм.

27. Найти среднее число столкновений в единицу времени молекул углекислого газа при температуре 100 ^oС, если средняя длина свободного пробега <>=870 мкм.

Решение. Число столкновений молекул газа в единицу времени связано со средней длиной свободного пробега соотношением

,

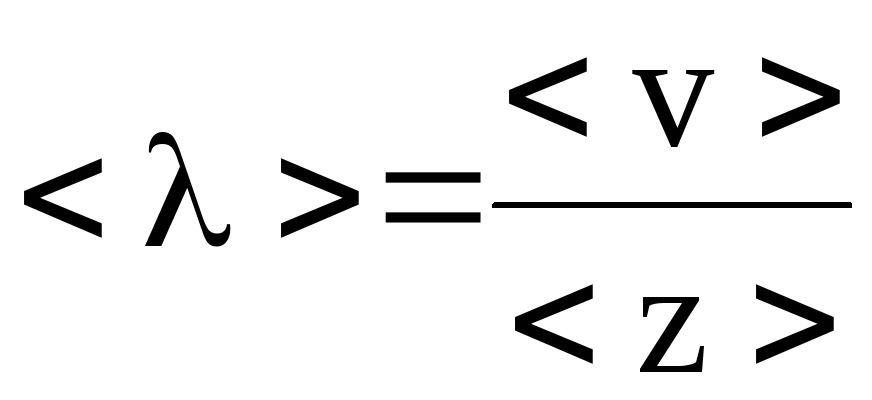где – средняя арифметическая скорость.

Следовательно,

.

Подставляя численные значения, имеем

с^-1.

Ответ: <z>=4,910⁵ с^-1.

28. При некотором давлении и температуре 0 ^oС средняя длина свободного пробега молекул кислорода 95 нм. Найти среднее число столкновений в единицу времени молекул кислорода, если давление кислорода уменьшить в 100 раз.

Решение. Среднее число столкновений в единицу времени

где – средняя арифметическая скорость молекул газа;

<> – средняя длина свободного пробега молекул.

При изменении давления газа длины свободного пробега обратно пропорциональны давлению:

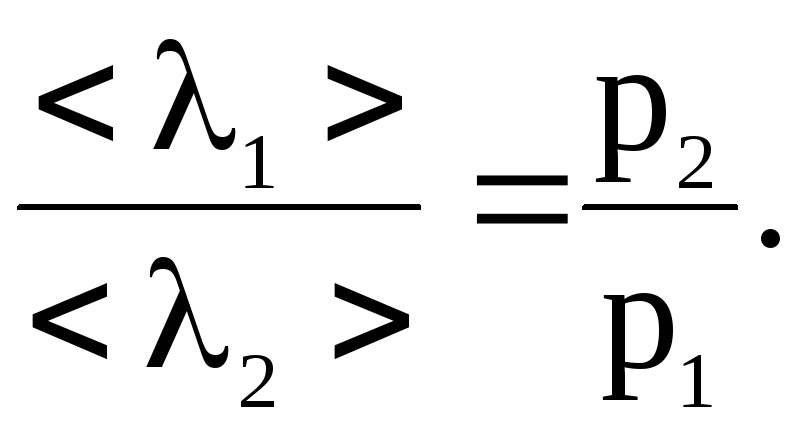
где ₁, ₂ – длина свободного пробега молекул газа при соответствующих давлениях p₁ и p₂.

В нашем случае:

.

Подставляя численные значения для <z>, имеем

.

Ответ: <z>=4,510⁷ с^-1.

29. Какая часть молекул кислорода при t= 0 ^oС обладает скоростями от 100 до 110 м/с?

Решение. Согласно распределению молекул по скоростям (закону Максвелла)

,

где u=v/v_в – относительная скорость;

v – данная скорость;

– наиболее вероятная скорость молекул;

u – интервал относительных скоростей, малый по сравнению со скоростью u.

Тогда искомая часть молекул, которую необходимо определить

.

В нашем случае v=100 м/с; Δv=10 м/с; наиболее вероятная скорость v=(2RT/)^1/2=376 м/с. Следовательно, u=v/v_в=100/376, u²=0,071; u=10/376; exp(–u²)=0,93.

Тогда

Ответ:ΔN/N=0,4%.

30. Сосуд, содержащий газ, движется со скоростью v_o, затем быстро останавливается. На сколько увеличится при этом средний квадрат скорости теплового движения молекул газа в случаях: одноатомного газа, двухатомного газа? Газ считать идеальным.

Решение. Воспользуемся законом сохранения энергии. Пусть M масса газа в сосуде. Двигаясь со скоростью v газ, как целое, обладает кинетической энергией

.

Эта формула определяет кинетическую энергию направленного движения молекул, в котором они участвуют вместе с сосудом. После остановки сосуда направленное движение молекул в результате их соударений со стенками сосуда очень скоро превратится в хаотическое.

Пренебрегая теплообменом между газом и стенками сосуда за рассматриваемый промежуток времени, можно газ считать изолированной системой. Тогда из закона сохранения энергии следует, что «исчезнувшая» кинетическая энергия направленного движения молекул W должна быть равна приросту энергии хаотического движений молекул (приросту внутренней энергии U):

W_к=U.

Определим внутреннюю энергию газа. Для идеального одноатомного газа это есть энергия поступательного хаотического движения молекул:

,

где m – масса молекулы;

N – число молекул в сосуде.

Имеем

Отсюда следует, что изменение внутренней энергии одноатомного газа при торможении

U=U₂-U₁=M[v²_кв2-v²_кв1],

где v_кв1,v_кв2 – средние квадратичные скорости молекул газа соответственно в начале и конце торможения.

Подставив в уравнение W_к=U значения W_к и U, получим первый ответ

v²_кв2–v²_кв1=v₀².

Внутренняя энергия идеального двухатомного газа складывается из энергий поступательного и вращательного движения молекул. При этом три степени свободы приходятся на поступательное движение и две – на вращательное. В соответствии с законом о равномерном распределении энергии по степеням свободы, три пятых кинетической энергии W пойдет на увеличение энергии поступательного движения молекул и две пятых – на увеличение энергии их вращательного движения. Таким образом, имеем:

.

Из последнего соотношения получим второй ответ:

.

Ответ: 1) ; .

31. Какая часть молекул водорода, находящегося при температуре T, обладает скоростями, отличающимися от наиболее вероятной скорости не свыше чем на 5,0 м/с? Задачу решить для двух значений T: 1) 400 К, 2) 900 К .

Решение. Распределение молекул по скоростям выражается законом Максвелла: число молекул N , относительные скорости которых лежат в интервале от u до u + u:

где N – полное число молекул газа;

– функция распределения Максвелла;

u=v/v_в – относительная скорость;

v – данная скорость;

v_в – наиболее вероятная скорость.

Закон распределения Максвелла оказывается справедливым при условии u<u. Поскольку в задаче идет речь о наиболее вероятной скорости, надо считать v=v_в. Следовательно, u=v/v_в=1 и вышенаписанное уравнение примет более простой вид:

.

Отсюда найдем ту часть молекул, относительные скорости которых лежат в интервале u:

Прежде чем производить расчеты, необходимо убедиться в том, что выполняется условие u<u. Так как u=v/v_в , то u=v/v_в.

Чтобы вычислить u , найдем сначала наиболее вероятную скорость при Т=400 К и Т=900 К по формуле:

:

v_в1=28,31400/0,002=1,8210³ м/с, v_в2=28,31900/0,002=2,7310³м/с.

Подставляя эти значения v_в и имея в виду, что v=10 м/с, поскольку в задаче идет речь о скоростях, лежащих в интервале от v_в=-5,0 м/с до v_в=5,0 м/с, получим:

u₁₌1/182, u₂=1/273.

Так как u=1, видим, что условие u<u выполняется для обеих температур.

Теперь найдем

N₁/N=4/((3,14)^1/22,7182)=0,0046, N₂/N=4/((3,14)^1/22,7273)=0,0030.

Таким образом, при увеличении температуры наиболее вероятная скорость молекул увеличивается, а число молекул, скорости которых лежат в одном и том же интервале около наиболее вероятной, уменьшается.

Ответ: N₁/N=0,0046, N₂/N=0,0030.

32. Какая часть молекул газа имеет скорости превышающие наиболее вероятную?

Решение. В условии задачи речь идет о молекулах, скорости которых заключены в интервале от наиболее вероятной скорости v до v+v, т.е. в бесконечно большом интервале скоростей. Таким образом, условие применимости закона распределения скоростей, заключающееся в том, что u<u, или v<v, здесь не выполняется. Поэтому от уравнения в форме:

надо перейти к дифференциальной форме этого закона

Полное число N молекул, относительные скорости которых лежат в заданном интервале от u₁ до u₂, найдем, интегрируя правую часть в этих пределах:

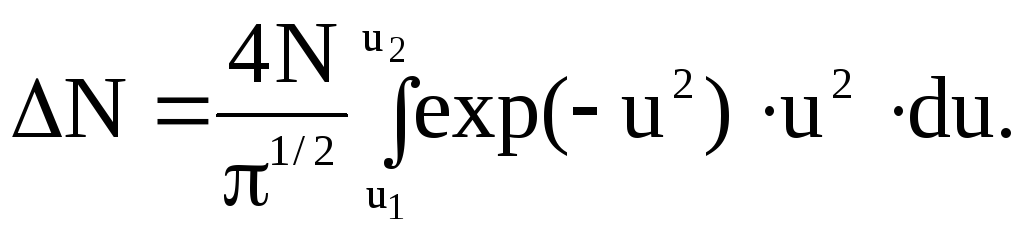
Данное уравнение является общей формой записи закона распределения скоростей молекул, справедливой для любых интервалов скоростей.

Учитывая, что относительная скорость u=v/v_в и что в нашей задаче v₁=v_в и v₂=4, получим: u₁=1, и u₂=. Следовательно, искомая часть молекул:

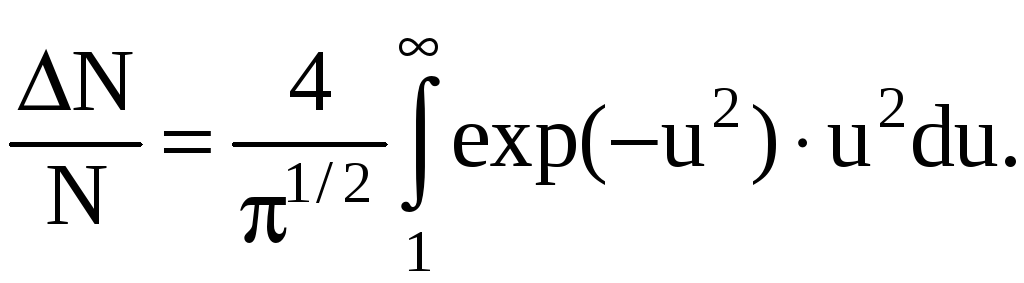
Чтобы избежать математических трудностей, связанных с нахождением неопределенного интеграла, воспользуемся тем очевидным фактом, что скорости всех молекул лежат в интервале от 0 до . Поэтому, если обозначить через N' число молекул, скорости которых меньше наиболее вероятной, т. е. лежат в интервале от 0 до 1, то можно записать:

.

Таким образом, вместо того, чтобы искать N/N можно найти

,

а затем вычислить N/N.

Так как зтот интеграл аналитически не вычисляется, то воспользуемся методом приближенного интегрирования. Для этого разложим подынтегральную функцию f(u)=exp(-u²)u² в ряд Маклорена:

exp(-u²)=1-u²/1+u⁴/2-u⁶/6+u⁸/24-... exp(-u²) u²=u²-u⁴/1+u⁶/2-u⁸/6+u¹⁰/24-...

Теперь, произведя интегрирование, имеем:

N'/N=4(1/3-1/5+1/14-1/54+1/264...)/^1/2.

Ограничиваясь первыми четырьмя членами разложения, найдем (с погрешностью, не превышающей 0,01):

N'/N=0,43.

Тогда

N/N=1-0,45=0,57.

Ответ: N/N=0,57.

33. Найти число столкновений <z>, которые происходят в течение секунды между всеми молекулами, находящимися в объеме V=1,0 мм³ водорода при нормальных условиях. Принять для водорода d=2,310^-10 м.

Решение. Число столкновений <z>, испытываемых одной молекулой за одну секунду, определяется по формуле

<z>= 2 ^1/2d²n²<v>V/2,

где d – эффективный диаметр молекулы;

n – концентрация молекул;

<v>= – средняя арифметическая скорость молекул газа.

Чтобы установить соотношение между величинами <z> и <z>, учтем, что если умножить число столкновений одной молекулы за одну секунду на число всех молекул N, то получим результат, превышающий в два раза искомое число <z>. Действительно, в одном столкновении участвуют сразу две молекулы, поэтому в число <z>N каждое столкновение входит дважды: один раз в счет столкновений одной из молекул данной пары, другой раз в счет столкновений второй молекулы. Следовательно, правильным будет выражение

<z>=<z>N/2=<z>nV/2,

где n=p/kT – концентрация молекул.

Подставив вместо <z>, n и <v> их значение, окончательно получим:

<z>=2 ^1/2d²p²V(8R/T)^1/2/2k²T.

Выразим входящие в формулу величины в единицах СИ, подставив их в формулу и выполнив вычисление, будем иметь

<z>=1,610²⁶ с^-1.

Ответ: <z>=1,610²⁶ с^-1.

34. Пылинки массой m=10^-18 г взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1%. Температура T воздуха во всем объеме одинакова и равна 300 К.

Решение. При равновесном распределении пылинок концентрация их зависит только от координаты y по оси, направленной вертикально. В этом случае к распределению пылинок можно применить формулу Больцмана

Так как в однородном поле силы тяжести U=mgy, то

По условию задачи, изменение Δn концентрации с высотой мало по сравнению с n (n/n=0,01), поэтому без существенной погрешности изменение концентрации n можно заменить дифференциалом dn.

Дифференцируя выражение по z, получим

Так как

,

то

dn=- mgndy/kT.

Отсюда находим интересующее нас изменение координаты:

dy=- kT dn/mgn.

Знак минус показывает, что положительным изменениям координаты (dy>0) соответствует уменьшение относительной концентрации (dn<0).

Знак минус опустим (в данном случае он несущественен) и заменим дифференциалы dy и dn конечными приращениями y и n:

y=kTn/mgn.

Выразив входящие в формулу величины в системе СИ, подставив их в эту формулу, произведем вычисления

y=1,3810^-233000,01/10^-219,81=4,2310^-3 м=4,23 мм.

Ответ: y=4,2310^-3 м.

35. Барометр в кабине летящего самолета все время показывает одинаковое давление p=79 кПа, благодаря чему летчик считает высоту h полета неизменной. Однако температура воздуха за бортом самолета изменилась с t=5^oC до t=1 ^oC. Какую ошибку h в определении высоты допустил летчик? Давление p у поверхности Земли считать нормальным.

Решение. Для решения задачи воспользуемся барометрической формулой

.

Барометр может показывать неизменное давление p при различных температурах T₁ и T₂ за бортом только в том случае, если самолет находится не на высоте h₁ (которую летчик считает неизменной), а на некоторой другой высоте h₂.

Запишем барометрическую формулу для двух случаев:

;

.

Найдем отношение p_o/p и обе части полученных равенств прологарифмируем:

Из полученных соотношений выразим высоты h₁ и h₁ и найдем их разность

Проверим, дает ли правая часть полученного равенства единицу длины:

Выразив величины в СИ, подставив их в полученную формулу, произведем вычисления:

Ответ: Δh=-28,5 м.

36. Средняя длина свободного пробега <> молекулы углекислого газа при нормальных условиях равна 40 нм. Определить среднюю арифметическую скорость <v> молекул и число <z> соударений, которые испытывает молекула в 1с.

Решение. Средняя арифметическая скорость молекул определяется по формуле

,

где  – молярная масса вещества.

Среднее число <z> соударений молекулы в одну секунду определяется отношением средней скорости <v> молекулы к средней длине ее свободного пробега <>:

Размерность полученных величин очевидна. Подставив значения входящих в формулы величин в СИ, будем иметь

<v>=362 м/с; <z>=9,0510⁹ с^-1.

Ответ: <v>=362 м/с; <z>=9,0510⁹ с^-1.

37. Вычислить удельные теплоемкости при постоянном давлении и при постоянном объеме неона и водорода, принимая газы за идеальные.

Решение. Между молярными и удельными теплоемкостями идеального газа при постоянном давлении и при постоянном объеме существует связь:

C_p=c_p и Cv=c_v,

где а

Таким образом, для удельных теплоемкостей имеем

а .

Зная, что неон одноатомный газ, то для него число степеней свободы i=3, m=2010^-3 кг/моль, а водород двухатомный газ для него число степеней свободы i=5, =2710^-3 кг/моль. Подставляя в каждую из выше записанных формул значения числп степеней свободы и значение универсальной газовой постоянной, вычисляем удельные теплоемкости для:

1) неона

2) водорода

;

.

Ответ: 1)

2) ; .

38. Найти отношение удельных теплоемкостей при постоянном давлении и постоянном объеме для кислорода.

Решение. Отношение удельных теплоемкостей при постоянном давлении и постоянном объеме идеального газа равно отношению его молярных теплоемкостей при постоянном давлении и постоянном объеме:

Зная, что молярные теплоемкости при постоянном давлении и при постоянном объеме связаны с числом степеней свободы и равны:

и

Для отношения удельных теплоемкостей будем иметь

Кислород двухатомный газ, следовательно, число степеней свободы i=5. Подставляя значение i в вышезаписанную формулу, имеем

Ответ: с_p/c_V=1,4.

39. Удельная теплоемкость некоторого двухатомного газа равна 14,7 кДж/(кгК). Найти молярную массу этого газа.

Решение. Известно, что удельная теплоемкость при постоянном давлении связана с молярной теплоемкостью газа:

Молярная теплоемкость при постоянном давлении

где i – число степеней свободы газа.

Таким образом:

Откуда

Подставляя в полученную формулу значения величин данных в условии задачи, с учетом того, что для двухатомного газа i=5 , будем иметь:

Ответ: μ=0,002 кг/моль.

40. Вычислить удельные теплоемкости при постоянном объеме и постоянном давлении смеси неона и водорода, если массовые доли неона и водорода составляют ₁=80% и ₂=20% соответственно. Удельные теплоемкости для неона с_v=6,2410² Дж/(кгК), с_p=1,0410³ Дж/(кгК); для водорода – с_v=1,0410⁴ Дж/(кгК), с_p=1,4610⁴ Дж/(кгК).

Решение. В общем случае количество тепла необходимого для нагревания смеси газов, например, при нагревании в условиях постоянного объема от температуры Т₁ до температуры Т₂ равна:

где с_v(см) – удельная теплоемкость смеси;

(m₁+m₂) – масса смеси;

(T₂ -T₁) – изменение температуры.

С другой стороны это количество тепла может быть вычислено по формуле:

где Q₁ и Q₁ – соответственно количество тепла, которое необходимо сообщить,чтобы изменить температуру неона и водорода в отдельности;

с_v1 и с_v2 – удельные теплоемкости неона и водорода при постоянном объеме;

m₁ и m₂ – массы неона и водорода.

Таким образом, имеем:

или

.

Откуда

где и – массовые доли неона и водорода соответственно.

Подставляя численные значения для удельной теплоемкости смеси неона и водорода при постоянном давлении, будем иметь:

Аналогично можно получить формулу для определения удельной теплоемкости смеси неона и водорода при постоянном давлении:

.

Подставляя численные значения для удельной теплоемкости смеси при постоянном давлении, будем иметь:

Ответ: ;

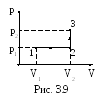
41. Кислород массой 2 кг занимает объем V₁=1 м³ и находится под давлением p₁=0,2 МПа (рис. 3.9). Газ был нагрет сначала при постоянном давлении до объема V₂=3 м³, а затем при постоянном объеме до давления p₃=0,5 МПа. Найти изменение внутренней энергии газа.

Решение. Изменение внутренней энергии газа

ΔU=c_vmΔT,

где c_v=iR/2μ – удельная теплоемкость при постоянном объеме;

μ – молярная масса газа;

ΔТ=(Т₃-Т₁) – изменение температуры газа в конечном и начальном состояниях;

i=5 – число степеней свободы (кислород двухатомный газ).

Температуру газа в начальном и конечном состояниях можно определить из уравнения Менделеева–Клапейрона:

.

Для начальной температуры

.

Для конечной температуры

Тогда изменение внутренней энергии газа

Подставляя численные значения, будем иметь

Дж.

Ответ: ΔU=3,25 кДж.

42. Кислород массой 2 кг занимает объем V₁=1 м³ и находится под давлением p₁=0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V₂=3 м³, а затем при постоянном объеме до давления p₃=0,5 МПа. Найти работу, совершенную газом, и теплоту, переданную газу (рис. 3.9).

Решение. Из уравнения Менделеева-Клапейрона

можно определить температуры, характерные для соответствующих состояний:

.

Таким образом, температура газа в начальном состоянии

T₁=p₁V₁/mR;

в промежуточном

T₂₌p₂V₂/mR;

в конечном

T₃=p₃V₃ /mR.

В процессе перехода газ совершал работу

A=A₁+A₂,

где A₁ – работа газа, совершенная при переходе в условиях постоянного давления;

A₂ – работа газа, совершенная при переходе в условиях постоянного объема.

Работа газа, совершенная при переходе в условиях постоянного давления определяется соотношением:

а работа газа, совершенная при переходе в условиях постоянного объема т.к. V=0.

Таким образом, в данном случае

Количество тепла, переданного газу равно сумме изменения его внутренней энергии и работы, совершенной им:

Известно, что изменение внутренней энергии газа пропорционально изменению его температуры, при этом

.

Следовательно, для изменения внутренней энергии газа при его переходе из начального в конечное состояние, имеем:

где Т=T₃–T₁.

Таким образом, для количества тепла переданного газу имеем:

Подставив численные значения величин, будем иметь:

Т₁=0,210⁶13210^–3/(8,3110³2)=385 К; Т₂=0,210⁶33210^–3/(8,3110³2)=1155 К; Т₃=0,510⁶33210^–3/(8,3110³2)=2888 К; U=528,31(2888–385)/(23210^–3)=3,2510³ Дж; A=28,31(1155–385)/3210^–3=0,410³ Дж; Q=3,2510³+0,410³=3,6510³ Дж.

Ответ: A=Дж; Q=3,6510³ Дж.

43. Масса 10 г кислорода находится под давлением 0,3 МПа и при температуре 10 ^oС. После нагревания при постоянном давлении газ занял объем V₂=10 л. Найти количество теплоты Q, полученное газом, и энергию теплового движения молекул газа W до и после нагревания.

Решение. Количество теплоты Q, полученное газом в процессе нагревания

где – молярная теплоемкость газа при постоянном давлении;

i=5 – число степеней свободы (кислород двухатомный газ);

R=8,31 Дж/(мольК) – универсальная газовая постоянная;

=0,032 кг/моль – молекулярная масса кислорода;

T₁ и T₂ – температуры газа в начальном и конечном состояниях. Для определения температуры газа в конечном состоянии воспользуемся соотношением между температурой и объемом газа, нагреваемого в условиях постоянного давления:

.

Откуда

Воспользовавшись уравнением Менделеева–Клапейрона, записанным в виде

находим объем газа в начальном состоянии:

Для конечной температуры будем иметь соотношение:

Подставляя численные значения, определяем конечную температуру газа:

Подставляя численные значения, находим количество теплоты, полученное газом в процессе нагревания:

Энергию теплового движения молекул газа можно определить по формуле

где C_V=iR/2 – молярная теплоемкость газа при постоянном объеме.

Таким образом, для энергии теплового движения молекул газа в начальном состоянии имеем:

в конечном состоянии

.

Ответ:Q=7,9 кДж; W₁=1,8 кДж; W₂=7,6 кДж.

44. Масса 12 г азота находится в закрытом сосуде объемом V=2 л при температуре t=10 ^oС. После нагревания давление в сосуде стало равным p₂=1,33 МПа. Какое количество теплоты Q сообщено газу при нагревании?

Решение. Так как объем газа не изменился, то сообщенное ему количество теплоты пошло на изменение его внутренней энергии Q=U, которое в свою очередь можно определить так:

U=mC_V(T₂–T₁)/=mC_VΔT/,

где Cv=iR/2 – молярная теплоемкость азота при постоянном объеме.

Следовательно,

U=miR(T₂–T₁)/2.

Для определения конечной температуры T воспользуемся тем, что при нагревании газа в условиях постоянного объема отношение давлений пропорционально отношению его температур в начальном и конечном состояниях

p₁/p₂=T₁/T₂.

Имеем

T₂=T₁p₂/p₁.

Начальное давление определяем из уравнения Менделеева–Клапейрона, записанного для первоначального состояния:

p₁V₁=mRT₁/. p₁=mRT₁/V₁.

Так как по условию задачи V₁=V, то для конечной температуры имеем:

T₂₌p₂V/mR.

Подставляя значение T₂ в формулу изменения внутренней энергии, которое равно количеству тепла, сообщенному газу, окончательно получим:

Q=imR(p₂V/mR-T₁)/2.

Размерность полученного результата очевидна. Численное значение Q равно

=4,13 кДж.

Ответ: Q=4,13 кДж.

45. Баллон с кислородом емкостью V=20 л при давлении p=100 ат и температуре t=7 ^oС нагревается до t=27 ^oС. Какое количество теплоты при этом поглощает газ?

Решение. Поскольку коэффициенты теплового расширения для твердых тел значительно меньше (приблизительно в сто раз), чем для газов, в условиях данной задачи можно пренебречь расширением баллона и считать процесс нагревания газа изохорным.

При изохорных процессах, подводимое к системе количество тепла идет на изменение ее внутренней энергии.

Из определения молярной теплоемкости следует, что элементарное количество теплоты, сообщенное телу при повышении его температуры на dT, равно:

dQ=C_VdT.

Число молей найдем из уравнения газового состояния (Менделеева–Клапейрона)

=m/=p₁V/RT₁.

Так как газ нагревается при постоянном объеме, то С=С_V, где С_V=iR/2.

Подставив значения  и С_V в формулу для элементарного количества тепла, получим:

Отсюда, интегрируя и учитывая при этом, что все величины i, p₁, T₁, V постоянные, найдем полное количество теплоты, поглощенное газом при нагревании от T₁ до T₂, которое численно и будет равно изменению его внутренней энергии:

Q=U=ip₁V(T₂–T₁)/(2T₁).

Проверив размерность, подставив в полученную формулу значения входящих величин в системе СИ, произведем вычисления:

U=59,810⁵210^–3(300-280)/(2280)=3510³ Дж=35 кДж.

Ответ: ΔU=35 кДж.

46. Баллон емкостью V=20 л с кислородом при давлении p=100 ат и температуре t₁=7^oС нагревается до t₂=27^oС. Какое количество теплоты при этом поглощает газ?

Решение. Поскольку коэффициенты теплового расширения для твердых тел значительно меньше (приблизительно в сто раз), чем для газов, в условиях данной задачи можно пренебречь расширением баллона и считать процесс нагревания газа изохорным.

При изохорических процессах, подводимое к системе количество тепла идет на изменение ее внутренней энергии.

Применим к рассматриваемому газу первое начало термодинамики:

Q=dU+A.

Поскольку при изохорном процессе газ не совершает работы, то A=0, а

Q=dU.

Для внутренней энергии идеального газа справедливо соотношение

U=imRT/2=ipV/2.

Отсюда для изменения внутренней энергии имеем

U=ip₁V(p₂/p₁-1)/2

Заменяя по закону Шарля для изохорного процесса отношение давлений p₂/p₁ отношением абсолютных температур T₂/T₁, получим:

Q=ip₁V(T₂/T₁-1)=ip₁VT₁(T₂-T₁)/2.

Все величины, кроме i, даны в условии задачи. Поскольку кислород является двухатомным газом, то число степеней свободы i=5.

Выразим входящие в формулу величины в единицах СИ: p=9,810⁶ Па, V=2,0010^-2 м³, T₁=280 К, T₂₌300 К.

Подставив эти значения и выполнив вычисление, получим

Q=59,810⁶2,0010^-2(300/280-1)/2=3,510³ Дж.

Ответ: Q=3,510³ Дж=35 кДж.

47. Какую работу надо совершить, чтобы, медленно сжимая при помощи поршня газ в цилиндре с хорошо проводящими тепло стенками, увеличить его давление в два раза? Начальное давление газа равно атмосферному p₁=760 мм рт.ст., начальный объем V₁=5,0 л. Во время сжатия давление и температура окружающего воздуха остаются постоянными. Весом поршня и трением пренебречь. Сколько тепла выделяется при сжатии газа?

Решение. Вначале выясним, каким процессом является сжатие газа в условиях задачи? Медленное протекание процесса и большая теплопроводность стенок цилиндра позволяют считать температуру газа равной температуре окружающей среды в течение всего процесса. Так как температура, согласно условию, остается неизменной, то сжатие газа следует считать изотермическим процессом.

Работа газа при изотермическом процессе определяется формулой:

.

Преобразуем ее применительно к данной задаче, используя уравнение газового состояния и закон Бойля–Мариотта:

.

Поскольку p₁<p₂, то A_г<0. Как и следовало ожидать, работа, совершенная газом при его сжатии, отрицательна. В этом случае положительной будет работа A_вн, совершенная внешними силами, сжимающими при помощи поршня газ в цилиндре:

.

Однако это выражение еще не является ответом, так как A_вн есть сумма двух работ: работы A силы, приложенной к поршню (например, силы руки), и работы A_атм силы атмосферного давления, т.е.

A_вн=A+A_атм.

По условию задачи искомой величиной является работа A. Величину же A_атм можно найти по формуле работы газа при изобарном процессе

A_атм=p₁(V₁-V₂),

поскольку атмосферное давление p₁ остается постоянным. При этом индексы у объемов проставлены так, чтобы работа A_атм, вычисленная по формуле, была положительной. Преобразуем эту формулу, учитывая, что газ в цилиндре сжимается изотермически:

A_атм=p₁V₁(1-V₂/V₁)=p₁V₁(1-p₁/p₂).

Искомая работа

A=A_вн-A_атм=p₁V₁(lnp₂/p₁-1+p₁/p₂).

Для определения количества теплоты, выделенного при сжатии газа, воспользуемся первым началом термодинамики. Поскольку при изотермическом процессе ( T=const ) изменение внутренней энергии равно нулю:

U=m C_VT/=0

из уравнения Q=U+A получаем, что количество теплоты, сообщенное газу, равно

Q=A_г=p₁V₁lnp₁/p₂=-p₁V₁lnp₁/p₂.

Величина Q оказалась отрицательной, что обусловлено выделением теплоты газом при его сжатии.

Выразим данные величины в единицах СИ:

V₁=5,010^-3 м³, p₁=1,0110⁵ Па, p₂/p₁=2. Подставив эти значения в формулы и выполнив вычисление, получим:

;

Q=-1,0110⁵5,010^-3ln2=-3,510² Дж=-0,35 кДж.

Ответ: A=0,10 кДж; Q=-0,35 кДж.

48. В цилиндре с плохо проводящими тепло стенками, закрытом сверху легко скользящим поршнем, площадь которого равна 20 см² и массой m_п=2,00 кг, находится воздух, который занимает объем V₁=1,00 л. На поршне лежит гиря массой m_г=8,00 кг. Если быстро убрать гирю, воздух расширится и поднимет поршень (рис. 3.10).

Определить работу расширения воздуха за время, в течение которого скорость поднимающегося поршня достигнет максимального значения v_max. Атмосферное давление p_o принять равным 1,00 ат.

Решение. Прежде всего, выясним характер процесса расширения воздуха в цилиндре. Учитывая, что, по условию, воздух расширяется быстро, а стенки цилиндра обладают плохой теплопроводностью, можно пренебречь теплообменом между воздухом и окружающей средой, т.е. считать процесс расширения воздуха адиабатическим.

Из условия задачи легко определить начальное давление p воздуха в цилиндре. На поршень в начальном состоянии действуют силы: сила тяжести поршня m_пg, вес гири, равный m_гg, сила атмосферного давления, равная p_oS, и сила давления воздуха, равная p₁S. Первые три силы направлены вниз, последняя сила – вверх. Из условия равновесия поршня имеем

p₁S=m_пg+m_гg+p_oS.

Откуда

p₁=(m_п+m_г)g/S+p₀=1,4710⁵ Па.

Условие задачи позволяет также определить давление p₂ воздуха в цилиндре в тот момент, когда скорость поднимающегося поршня достигнет максимума. Поскольку воздух расширяется адиабатически, из уравнения Пуассона pV=const следует, что его давление, а значит, и сила давления на поршень будут уменьшаться. После того как сняли с поршня гирю, сила давления воздуха на поршень снизу была сначала больше, чем сумма сил mg+pS, действующих на него сверху, но спустя некоторый промежуток времени, в течение которого поршень двигался ускоренно, силы, приложенные к поршню, окажутся снова в равновесии.

Именно в этот момент скорость поршня достигнет значения v_max, так как при дальнейшем увеличении объема воздуха в цилиндре его давление станет меньше суммы давлений сил m_пg+p₀S. Теперь равнодействующая сил, приложенных к поршню, окажется направленной вниз и скорость поршня будет убывать. Таким образом, из условия равновесия сил, соответствующего максимуму скорости поршня:

p₂S=m_пg+p₀S,

находим

p₂=m_пg/S+p₀=1,0810⁵ Па.

Теперь, зная начальное p₁ и конечное p₂ давления воздуха в адиабатическом процессе, а также начальный объем V₁, легко найти работу расширения газа:

.

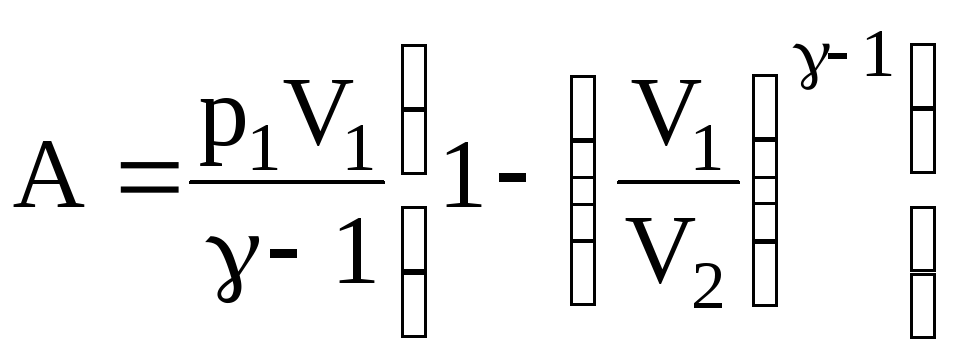Неизвестное отношение объемов выразим через отношение давлений

.

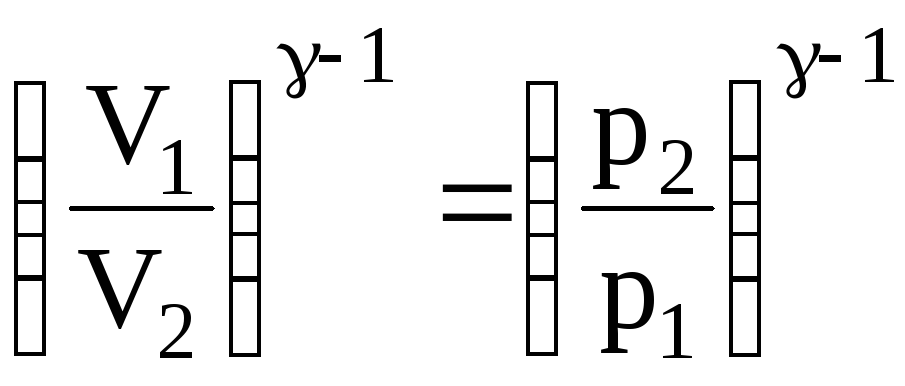Таким образом, имеем

.

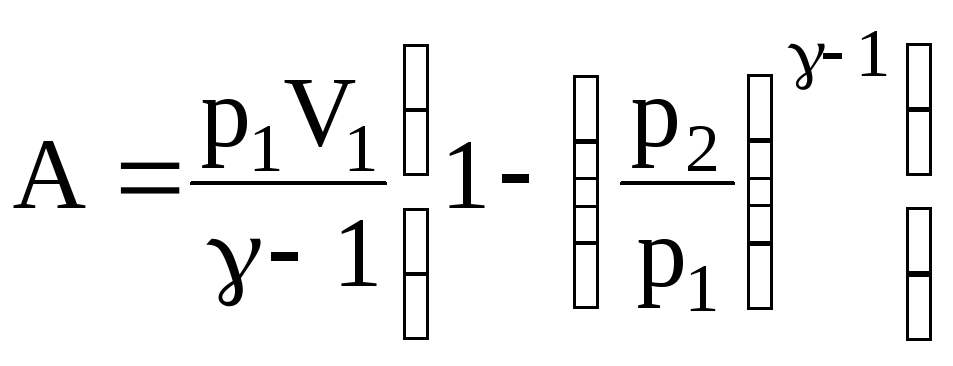Поскольку воздух является смесью двухатомных газов – азота и кислорода, определим показатель адиабаты, отношение его теплоемкостей, как для двухатомного газа i=5:

=C_p/C_V=(i+2)/i=(5+2)/5=1,4.

Подставив числовые значения величин в единицах СИ, получим

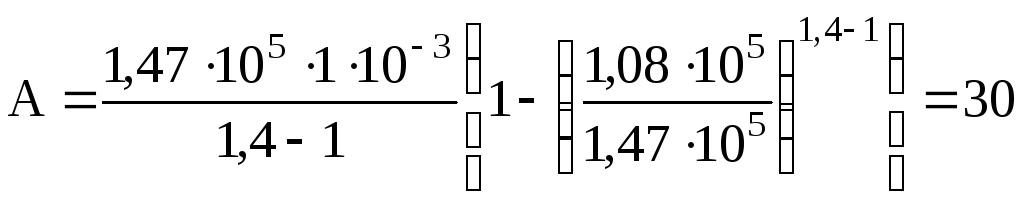Дж.

Ответ: A=30 Дж.

49. В цилиндре под поршнем находится водород массой m=0,02 кг при температуре T₁=300 К. Водород сначала расширялся адиабатно, увеличив свой объем в пять раз, а затем был сжат изотермически, причем объем газа уменьшился в пять раз (рис. 3.11). Найти температуру в конце адиабатного расширения и работу, совершаемую газом при этих процессах.

Решение. Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением

или ,

где  – отношение теплоемкостей газа при постоянном давлении и постоянном объеме;

Отсюда получаем следующее выражение для конечной температуры:

Работа газа при адиабатном расширении может быть определена по формуле

A=mC_V(T₁-T₂)/,

где C_V – молярная теплоемкость газа при постоянном объеме.

Работа A₂ газа при изотермическом процессе может быть выражена в виде:

A₂=mRT₂ln(V₃/V₂)/, или A₂=mRT₂ln(1/n₂)/,

где

Выразив все величины в единицах СИ, подставив их в соответствующие формулы, произведем вычисления, учитывая, что для водорода как для двухатомного газа =1,4, i=5 и m=210^-3 кг/моль, получим:

T₂=157 К; A₁=29,8 кДж; A=-21 кДж.

Знак минус показывает, что при сжатии работа совершается над газом внешними силами.

Ответ: T₂=157 К; A₁=29,8 кДж; A=-21 кДж.

5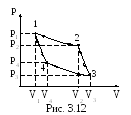0. Тепловая машина работает по обратимому циклу Карно. Температура теплоотдатчика T₁=500 К (рис. 3.12). Определить термический КПД  цикла и температуру T₂ теплоприемника тепловой машины, если за счет каждого килоджоуля теплоты, полученной от теплоотдатчика, машина совершает работу A=350 Дж.

Решение. Термический КПД тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу. Термический КПД выражается формулой

=A/Q₁=(Т₁-Т₂)/Т₁,

где Q – теплота полученная от теплоотдатчика;

A – работа, совершенная рабочим телом тепловой машины;

T₁ – температура теплоотдатчика;

T₂ – температура теплоприемника.

Зная КПД цикла, по формуле T₂=T₁(1-) можно определить температуру теплоприемника.

В условии задачи все величины представлены в единицах СИ, подставив их в соответствующие формулы, произведя вычисления, получим:

=350/1000=0,35; T₂=500(1-0,35)=325 К.

Ответ: =0,35; T₂=325 К.

5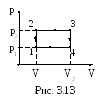1. Идеальный трехатомный газ совершает цикл, состоящий из изохоры (1–2), изобары (2–3), изохоры (3–4) и изобары (4–1). Определить КПД цикла, если V₁=1,00 л, V₂=2,00 л, p₁=1,0 атм, p₂=2,0 атм. Считая величины V₁, V₂, p₁, p₂ переменными, принимающими любые положительные значения, найти предельный (наибольший) КПД данного цикла (рис. 3.13).

Решение. Рассмотрим процессы цикла по порядку.

1. Первый процесс. Объем V₁ газа сохраняется, при этом давление его увеличивается от p₁ до p₂. Так как при изохорном процессе давление газа пропорционально его абсолютной температуре, видим, что температура газа здесь повышается. Следовательно, газ при этом получает (от нагревателя) количество тепла Q₁₂.

2. Второй процесс. Давление p₂ газа сохраняется, объем же увеличивается от V₁ до V₂, при этом газ совершает работу, равную

A₂₃=p₂(V₂-V₁).

Так как при изобарном процессе объем газа пропорционален абсолютной температуре, видим, что температура газа и в этом процессе повышалась. Следовательно, и здесь газ получил количество теплоты Q₂₃.

3. Третий процесс. Процесс идет изохорно (V₂=const), давление газа уменьшается от p₂ до p₁, что означает понижение температуры. Следовательно, газ при этом отдает (холодильнику) количество теплоты Q₃₄.

4. Четвертый процесс. При постоянном давлении p₁ газ сжимается от объема V₂ до объема V₁ и совершает при этом отрицательную работу

А₄₁=p₁(V₁–V₂)=-p₁(V₂-V₁).

Уменьшение объема при изобарном процессе связано с понижением температуры газа. Следовательно, здесь, как и в предыдущем случае, газ отдает (холодильнику) некоторое количество тепла Q₄₁.

Теперь можно приступить к вычислению КПД цикла по формуле:

=A/Q₁=(Q₁-Q₂)/Q₁=(T₁-T₂)/T₁.

где A – работа, совершенная рабочим веществом в течение цикла;

Q₁ – количество теплоты, полученное за это время рабочим веществом;

Q₂ – количество теплоты, отданное при этом холодильнику;

T₁ и T₂ – наивысшая и наинизшая температуры рабочего вещества.

Работа газа совершается во втором и четвертом процессах и равна

A=A₂₃+A₄₁=(p₂-p₁)(V₂-V₁).

Количество теплоты Q, сообщенное газу при его нагревании, найдем на основании первого начала термодинамики. Учитывая, что газ получает теплоту в первом и втором процессах:

Q=U+A.

Изменение внутренней энергии U при переходе газа из состояния 1 в состояние 3 вычислим как разность значений U₃ и U₁:

U=U₃-U₁=imR(T₃-T₁)/2

На основании уравнения газового состояния, можно записать:

U=i(p₂V₂-p₁V₁)/2.

Подставив вместо U и A₂₃ их значения в формулу для определения Q₁, получим

Q₁=i(p₂V₂-p₁V₁)/2+p₂(V₂-V₁).

Наконец найдем КПД цикла

Подставив числовые значения величин p₁, p₂, V₁, V₂, из условия задачи и учитывая, что газ трехатомный и, следовательно, i=6, получим:

.

Чтобы определить наибольший КПД цикла, выразим количество теплоты, сообщенное газу, через молярные теплоемкости C_p и C_V

Q=Q₁+Q₂=C_V(T₂-T₁)+C_p(T₃-T₂).

С помощью уравнения Менделеева–Клапейрона, записав его для каждого из трех состояний 1, 2, 3 преобразуем вышенаписанную формулу для Q₁:

Q₁=((p₂–p₁)V₁C_V/R)+((V₂-V₂)p₂C_p/R).

Подставив значения A и Q₁ в формулу для КПД, получим

Чтобы упростить исследование, разделим числитель и знаменатель на произведение p₂V₂ и введем обозначения =p₁/p₂, =V₁/V₂:

Заметим, что согласно условию каждая из величин  и  может принимать любые значения в интервале от 0 до 1.

При произвольном фиксированном значении  выражение приобретает вид:

,

где K₁, K₂, K₃ – постоянные положительные величины.

Из полученного выражения видно, что () – убывающая функция. Следовательно, она принимает наибольшее значение при =0.

При любом фиксированном значении  имеем

где К₄, К₅, К₆ – постоянные положительные величины.

Из последнего выражения видно, что () – убывающая функция. Значит, ее наибольшему значению соответствует =0.

Сопоставляя полученные результаты, приходим к выводу, что, положив в формуле для КПД =0, =0, найдем предельное значение _пред:

_пред=R/C_p=2/(i+2)=2/(6+2)=0,25.

Ответ: η=0,09; _пред=0,25.

52. Цикл Карно, совершаемый смесью жидкости и пара, происходит в том же температурном интервале, что и цикл, рассмотренный в задаче 50. Определить КПД цикла Карно.

Решение. КПД цикла Карно, состоящего из двух изотерм и двух адиабат, не зависит от того, какое рабочее вещество совершает этот цикл, и равен

_К=(Т₁-Т)/Т₁.

Таким образом, задача сводится к определению наивысшей и наинизшей температур газа в условиях задачи 50.

Было уже выяснено, что газ нагревался при совершении первого и второго процессов и охлаждался при совершении третьего и четвертого процессов. Следовательно, наивысшей температурой газ обладал после второго процесса, наинизшей – вначале первого или в конце четвертого. Сохраняя обозначения предыдущей задачи, можно записать на основании уравнения газового состояния:

T₁=T₃=p₂V₂/R, T₂=T₁=p₁V₁/R.

Подставив эти значения T₁ и T₂ в формулу для определения КПД цикла Карно, получим

_К=(p₂V₂–p₁V₁)/p₂V₂.

Ответ: η=(p₂V₂-p₁V₁)/p₂V₂.

53. Тепловая машина работает по циклу Карно, КПД которого =0,25. Каков будет холодильный коэффициент ' машины, если она будет совершать тот же цикл в обратном направлении? Холодильным коэффициентом называется отношение количества теплоты, отнятого от охлаждаемого тела, к работе двигателя, приводящего в движение машину.

Решение. КПД любого цикла, в том числе и цикла Карно, можно определить по формуле

=A/Q₁=(Q₁-Q₂)/Q₁.

Особенностью цикла Карно является его обратимость: процесс может протекать как в прямом, так и в обратном направлении. При обратном цикле Карно рабочее вещество будет, расширяясь по изотерме T₂=const, отбирать от холодильника количество теплоты Q₂ и, сжимаясь по изотерме T₁=const, отдавать нагревателю количество теплоты Q₁. При этом работа, совершенная рабочим веществом за один цикл, будет отрицательной (положительная работа расширения меньше по модулю отрицательной работы сжатия). В этом случае положительной будет работа A двигателя, приводящего в действие машину.

Согласно определению холодильного коэффициента, запишем

'=Q₂/A.

Чтобы его определить, исключим из формулы КПД цикла Карно величину Q₁=A+Q₂:

=A/(A+Q₂).

Выполнив преобразования, получим:

1/=(A+Q₂)/A=1+Q₂/A=1+'

или

'=1/-1.

Подставив численные значения, будем иметь

'=1/0,25-1=3, или '=300%.

Ответ: '=3, или '=300%.

54. Идеальный двухатомный газ, содержащий количество вещества =1 моль, находится под давлением p₁=250 кПа и занимает объем V₁=10 л. Сначала газ изохорно нагревают до температуры T₂=400 К. Далее, изотермически расширяя, доводят его до первоначального давления (рис. 3.14). После этого путем изобарного сжатия возвращают газ в начальное состояние. Определить термический КПД цикла.

Решение. Для наглядности решения задачи можно построить график цикла, который будет состоять из изохоры, изотермы и изобары, с характерными точками начала и конца соответствующих процессов: 1, 2, 3. термический коэффициент полезного действия любого цикла определяется выражением

=(Q₁-Q₂)/Q₁=1-Q₂/Q₁,

где Q₁ – количество теплоты, полученное газом за цикл от нагревателя;

Q₂ – количество теплоты, отданное газом за цикл охладителю (холодильнику);

(Q₁-Q₂)=A – работа, совершаемая газом за цикл.

Рабочее вещество (газ) получает тепло Q₁ от нагревателя, в рассматриваемом случае, при переходе из состояния 1 в состояние 2 (изохорно) Q₁₂ и при переходе из состояния 2 в состояние 3 (изотермически) Q₂₃. Таким образом:

Q₁=Q₁₂+Q₂₃.

Количество теплоты, полученное газом при переходе из состояния 1 в состояние 2 (при изохорическом процессе):

Q₁₂=C_V(T₂-T₁),

где C_V – молярная теплоемкость при постоянном объеме;

 – количество вещества;

T₁ – температура газа в начальном состоянии (1);

T₂ – температура газа в конечном состоянии (2).

Температуру T₁ начального состояния газа найдем, воспользовавшись уравнением Менделеева–Клапейрона:

T₁=p₁V₁/(R).

Количество теплоты, полученное газом при переходе из состояния 2 в состояние 3 (при изотермическом процессе), равно

Q₁₂=RT₂ln(V₂/V₁),

где V₂ – объем газа при температуре T₂ и давлении p₁ в состоянии 3.

Количество теплоты, отданное газом при переходе из состояния 3 в состояние 1 (при изобарическом процессе)

Q₂=Q₃₁=C_p(T₂-T₁),

где C_p – молярная теплоемкость газа при постоянном давлении.

Подставим найденные значения Q₁ и Q₂ в формулу для термического коэффициента полезного действия, будем иметь

В полученном выражении заменим отношение объемов, согласно закону Гей-Люссака, отношением температур V₂/V₁=T₂/T₁.

Выразив C_V и C_p через число степеней свободы молекул газа C_V=iR/2 и Cp=(i+2)R/2, после сокращения на  и R/2, получим:

Подставив значения i, T₁, T₂ и R и произведя вычисление, найдем

.

Ответ: =0,041=4,1%.

55. Нагреватель тепловой машины, работающий по обратимому циклу Карно, имеет температуру t₁=200 ^oС. Определить температуру T₂ охладителя, если при получении от нагревателя количества теплоты Q₁=1 Дж машина совершает работу A=0,4 Дж. Потери на трение и теплоотдачу не учитывать.

Решение. Температуру охладителя найдем, воспользовавшись выражением для термического КПД машины, работающей по циклу Карно:

=(T₁-T₂)/T_1.

Отсюда

T₂=T₁(1-).

Термический КПД тепловой машины выражает отношение количества теплоты, которое превращено в механическую работу A, к количеству теплоты Q₁, которое получено рабочим телом тепловой машины из внешней среды (от нагревателя):

=A/Q₁.

Подставив это выражение, найдем

T₂=T₁(1-A/Q₁).

Учтя, что Т₁=473 К, после вычисления будем иметь

T₂=473(1-0,4/1)=284 К.

Ответ: T₂=284 К.

56. Найти изменение энтропии при нагревании воды массой m=100 г от температуры t₁=0 ^oС до температуры t₂=100 ^oC и последующем превращении воды в пар той же температуры.

Решение. Полное изменение энтропии в данном случае равно сумме изменения энтропии при нагревании воды и изменения энтропии системы при ее превращении в пар

S=S'+S''.

Найдем изменение энтропии при нагревании воды. Как известно, изменение энтропии выражается общей формулой

При бесконечно малом изменении температуры dT нагреваемого тела затрачивается количество теплоты

Q=mcdT,

где m – масса тела;

c – его удельная теплоемкость.

Подставив выражение Q для изменения энтропии при нагревании воды, будем иметь

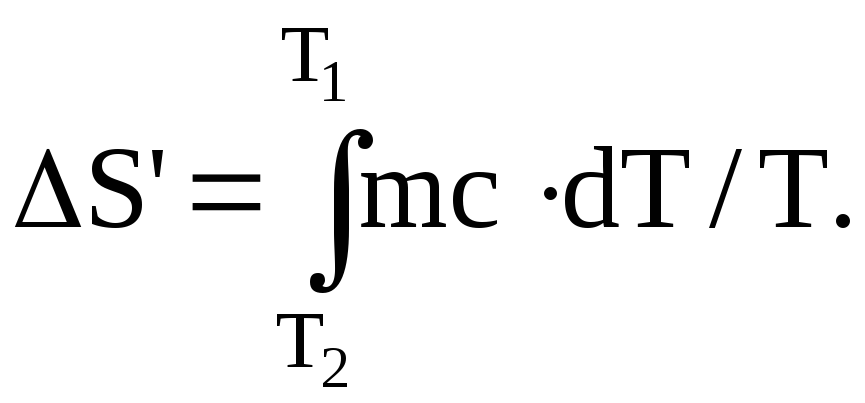
После интегрирования получим

S=mcln(T₂/T₁).

Изменение энтропии во время превращения воды в пар при постоянной температуре

где Q – количество теплоты, переданное при превращении нагретой воды в пар той же температуры.

Подставив выражение количества теплоты Q=m, где  – удельная теплота парообразования, получим

S''=m/T.

Таким образом, искомое полное изменения энтропии будет равно

S=mcln(T₂/T₁)+m/T.

Подставив численные значения величин в единицах системы СИ, произведем вычисление

S=10010^-34,1910³ln(373/273)+2,2610⁶10010^-3/373=736 Дж/К.

Ответ: S=736 Дж/К.

57. Определить изменение энтропии при изотермическом расширении кислорода массой m=10 г от объема V₁=25 л до объема V₂=100 л.

Решение. Так как процесс изотермический, то в общем выражении для изменения

Проинтегрировав это выражение, получим

S=Q/T.

Количество теплоты Q, полученное газом, найдем из первого начала термодинамики:

Q=U+A.

Для изотермического процесса U=0, следовательно Q=A, a работа для этого процесса определяется по формуле

A=(m/)RTlnV₂/V₁.

С учетом этого будем иметь

S=(m/)RlnV₂/V₁.

Подставив числовые значения, в единицах системы СИ и произведя вычисления, получим

S=(1010^-3/3210^-3)8,31ln100/25=3,6 Дж/К.

Ответ: ΔS=3,6 Дж/К.

58. Струя водяного пара при температуре 100 ^oС, направленная на глыбу льда, имеющую массу m=5 кг и температуру 0 ^oС, растопила ее и нагрела получившуюся воду до температуры 50 ^oС. Найти массу израсходованного пара и изменение энтропии при описанных процессах.

Решение. Количество теплоты, необходимое для плавления льда и для нагревания полученной холодной воды, равно количеству теплоты, выделившейся при превращении пара в воду той же температуры и последующем охлаждении полученной горячей воды. Составим уравнение теплового баланса:

m₁+cm₁(-t₁)=m₂r+cm₂(t₂-),

где m₁ – масса льда;

m₂ – масса пара;

 – удельная теплота плавления льда;

r – удельная теплота парообразования воды;

с – удельная теплоемкость воды;

 – температура смеси;

t₁ – температура плавления льда;

t₂ –температура кипения воды.

Решая уравнение относительно m₂, получаем

.

Подставим числовые значения величин в единицах СИ: =3,3510⁵ Дж/кг, r=2,2510⁶ Дж/кг, c=4,1910³ Дж/(кгград), m₁=5 кг, произведем вычисление, будем иметь

кг.

Изменение энтропии S равно сумме изменений энтропии при таянии льда (S₁), при нагревании получившейся холодной воды (S₂), при превращении пара в воду той же температуры (S₃) и, наконец, при охлаждении полученной горячей воды до окончательной температуры смеси (S₄).

Изменение энтропии при переходе системы из состояния 1 в состояние 2 выражается формулой

Найдем изменение энтропии при каждом из описанных процессов:

1) при таянии льда температура T сохраняет постоянное значение, равное 273 К. Вынося постоянную температуру за знак интеграла, получаем

S=Q₁/T,

где Q₁=m₁ – количество теплоты, необходимое для таяния льда.

Следовательно,

S₁=m₁/T.

2) при нагревании воды на dT требуется количество теплоты, равное:

Q₂=cm₁dT.

Следовательно, изменение энтропии при нагревании воды выразится так:

3) при превращении пара в воду той же температуры изменение энтропии может быть найдено на основании тех же соображений, что и в случае таяния льда, т.е.

S₃=Q/T=-rm₂/T.

Изменению энтропии приписывается знак "минус", так как теплота выделяется;

4) наконец, изменение энтропии, происходящее при охлаждении полученной горячей воды, найдем на основании тех же рассуждений, что и в случае нагревания воды, т.е.

S₄=-cm₂lnT₂/T₁.

Знак "минус" – так как теплота отбирается.

Полное изменение энтропии рассмотренных процессов будет равно:

S=S₁+S₂+S₃+S₄,

или

S=m₁/T₁+cm₁ln/T₁–rm₂/T₂–cm₂ln/T₂.

Подставляя численные значения величин в единицах СИ, произведя вычисления, имеем

S=2,2710³ Дж/К.

Ответ: m₂=1,11 кг; S=2,2710³ Дж/К.

59. Исходя из второго начала термодинамики, вывести формулу для КПД цикла Карно.

Решение. Наиболее общим выражением второго начала термодинамики является выражение вида:

S0.

Поскольку цикл Карно представляет собой обратимый процесс, из этой формулы следует, что полное изменение энтропии изолированной системы нагреватель–рабочее вещество–холодильник равно нулю:

S=0.

Согласно свойству аддитивности, полное изменение энтропии системы S будет складываться из изменений энтропии нагревателя S₁, рабочего вещества S' и холодильника S₂:

S=S₁+S'+S₂.

Рассмотрим эти изменения энтропии за один цикл. Так как рабочее вещество, совершив цикл, вернется в первоначальное состояние, а энтропия является функцией состояния, то она примет также первоначальное значение, т.е. S'=0. Следовательно, имеем

S=S₁+S₂=0.

Изменение энтропии нагревателя S₁ и холодильника S₂ можно определить по формуле

Нагреватель отдает рабочему веществу количество теплоты Q₁ при постоянной температуре T₁, переходя при этом из некоторого состояния 1 в состояние 2. Поэтому приращение Q берем со знаком "минус":

Холодильник получает от рабочего тела количество теплоты Q₂ при температуре T₂, переходя из некоторого состояния 3 в состояние 4. Следовательно,

Подставив эти значения S₁ и S₂ в формулу для полного изменения энтропии, будем иметь

-Q₁/T₁+Q₂/T₂=0 или -Q₁/T₁=-Q₂/T₁.

Откуда

-Q₂/Q₁=-T₂/T₁.

Прибавив к обеим частям равенства по единице, найдем

=(Q₁-Q₂)/Q₁=(T₁-T₂)/T₁.

Ответ: .

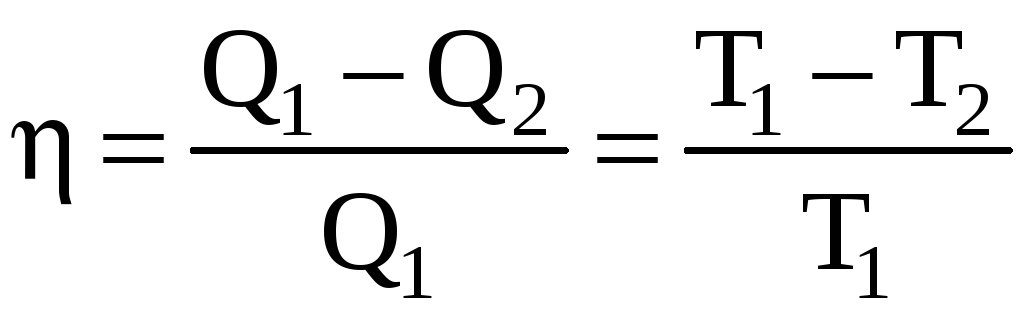60. Теплоизолированный сосуд разделен на две равные части перегородкой, в которой имеется закрывающееся отверстие. В одной половине сосуда содержится m=10,0 г водорода. Вторая половина откачана до высокого вакуума. Отверстие в перегородке открывают, и газ заполняет весь объем. Считая газ идеальным, найти приращение его энтропии.

Решение.Расширение газа здесь является необратимым процессом. Поэтому было бы ошибкой применить для данного процесса формулу

Воспользуемся тем, что энтропия – функция состояния и ее изменение полностью определяется начальным и конечным состояниями системы, независимо от того процесса, в ходе которого система перешла из начального состояния в конечное. Поэтому представим такой процесс расширения газа, который переводил бы его в то же самое конечное состояние, но являлся бы обратимым процессом. Найдя по вышеприведенной формуле приращение энтропии в таком обратимом процессе, мы решим поставленную задачу.

Так как данный газ изолирован от окружающей среды (Q=0, A=0), то его внутренняя энергия U, как это следует из первого начала термодинамики, должна оставаться постоянной. При этом будет постоянной и температура идеального газа во время его расширения. Значит, в качестве обратимого процесса, переводящего газ в то же конечное состояние, что и данный процесс, можно рассматривать процесс обратимого изотермического расширения, в ходе которого объем газа увеличивается в два раза. Так как в этом процессе T=const, U=0 и, следовательно, Q=A.

Работа, совершаемая газом при изотермическом процессе определяется соотношением

A=mRT/lnV₂/V₁.

Таким образом, для изменения энтропии имеем

Выразим входящие в формулу величины в единицах СИ: m=1,0010^-3 кг, =2,0010^-3 кг/моль, R=8,3 Дж/(мольК).

Выполнив вычисление, получим

Дж/К.

Ответ: S=29 Дж/К.

61. Кислород, масса которого m=200 г, нагревают от температуры t=27 ^oС до температуры t=127 ^oС. Найти изменение энтропии, если известно, что начальное и конечное давления одинаковы и близки к атмосферному.

Решение. По условию задачи кислород в данном случае подчиняется уравнениям идеального газа. Характер процесса нагрева неизвестен. Но изменение энтропии системы при переходе из одного состояния в другое определяется только параметрами этих состояний и не зависит от характера процесса.

Найти изменение энтропии можно, рассмотрев произвольный обратимый процесс, в результате которого систему (в данном случае идеальный газ) можно перевести из какого–либо состояния 1 в состояние 2, совершив изобарное расширение. Кроме того, из состояния 1 в состояние 3, совершив изотермическое расширение, а затем, последующим изохорным нагреванием из состояния 3 в состояние 2. Тогда при переходе системы из состояния 1 в состояние 2 по первому пути, изменение энтропии системы можно определить по формуле

где Q_p=mC_pdT/ .

Изменение энтропии системы при переходе из состояния 1 в 2 по второму пути, равно сумме изменения энтропии при переходе из состояния 1 в состояние 3 и из состояния 3 в состояние 2, т.е.

где Q_T=A=pdV, Q_V=mC_VdT/.

При изобарном процессе – C_p=(i + 2)/2, где i число степеней свободы.

Имеем

S=S₂–S₁=m(i+2)R/2lnT₂/T₁.

Легко проверить, что результат не изменится и при переходе 1–3–2.

Подставляя выражения Q_T и Q_V с учетом того, что при изотермическом процессе p=p₁V₁/V=mRT₁/(V), получим

S=mR/lnV₃/V₁ + mC_V /mlnT₂/T₃.

Учитывая, что T₃=T₁, V₃=V₂, T₂/T₁=V₂/V₁ и (R+C_V)=C_p, получим

S=S₂-S₁=m(i+2)R/2lnT₂/T₁.

Подставив значения величин в единицах системы СИ, произведя вычисление, имеем

S=S₂-S₁=20010^-3(5+2)8,31/(23210^-3)ln400/300=52 Дж/К.

Ответ: ΔS=52 Дж/К.

62. Теплоизолированный сосуд, разделенный на две разные части (V₁=2 л, V₂=3 л), наполнен идеальным газом. В первой части газ находится под давлением p₁=10⁵ Па и температуре t₁=27 ^oC; во второй части под давлением p₂=510⁵ Па и той же температуре. Найти изменение энтропии всей системы после удаления перегородки и установления равновесного состояния. Изменится ли ответ, если в объемах V₁ и V₂ находятся разные газы?

Решение. Рассматриваемая система изолирована – теплообмен не происходит, внешние силы не действую. После удаления перегородки начнется заведомо необратимый самопроизвольный процесс, в результате которого во всем сосуде будет находиться однородный газ под некоторым давлением p₀, причем p₁<p₀<p₂. Вся система не участвует в теплообмене, ни один из газов не совершает работы. Следовательно, в конечном состоянии суммарная внутренняя энергия системы, а значит, и средняя энергия, приходящаяся на долю одной молекулы, будут такими же, как и до удаления перегородки. Поэтому температура газа остается постоянной и равной T₁.

Энтропия системы в результате этого необратимого процесса увеличивается. Изменение ее определяется только начальным и конечным состояниями системы. Чтобы найти это изменение, надо представить себе любой обратимый процесс, переводящий данную систему из начального состояния в конечное.

Представим себе, что сосуд разделен поршнем, который перемещается до тех пор, пока давление с обеих его сторон не станет одинаковым и равным p₀ (газ в левой части сосуда сжимается, в правой – расширяется). Чтобы процесс был изотермическим и обратимым, во-первых, должна быть нарушена теплоизоляция сосуда: газ в левой части сосуда должен отдавать теплоту, в правой – получать. Во-вторых, поршень должен двигаться медленно, следовательно, на него должна действовать внешняя сила, компенсирующая результирующую силу давления газов.

После выравнивания давлений обе части газа окажутся в одинаковых равновесных состояниях; поэтому если убрать перегородку (поршень), то энтропия системы не изменится. Следовательно, искомое изменение энтропии системы равно сумме изменений энтропии каждой части газа в отдельности при описанном изотермическом перемещении поршня:

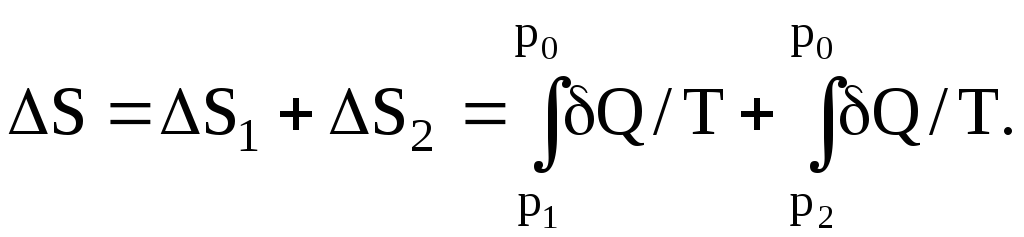
При изотермическом процессе

Q_T=A_T=pdV=-Vdp.

Последнее из равенств следует из того, что d(pV)=0 при pV=const.

Тогда

Выражая в интегралах текущий объём из уравнений изотермических процессов, записанных для начального и текущего состояний, получим

S=(p₁V₁ln(p₁/p₀)+p₂V₂ln(p₂/p₀))/T₁.

Давление p₀ может быть найдено из уравнений изотермических процессов для каждой части газа:

p₁V₁=p₀V'₁; p₂V₂=p₀V'₂,

где V₁' и V₂' – объем каждой части газа после выравнивания давлений, причем V'₁+V'₂=V₁+V₁.

Тогда почленное сложение уравнений дает:

p₁V₁+p₂V₂=p₀(V₁+V₂),

откуда

p₀=(p₁V₁+p₂V₂)/(V₁+V₂).

Следовательно, для полного изменения энтропии будем иметь:

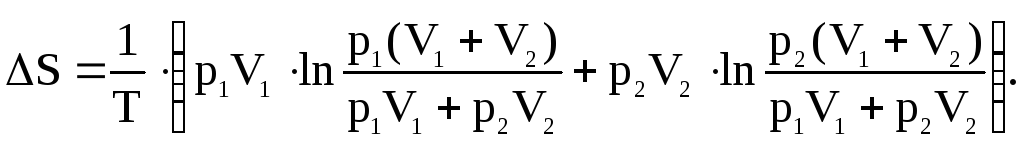
Выразив все величины в единицах СИ, подставив их значения, произведем вычисление

ΔS=1,1 Дж/К.

Если бы в объемах V₁ и V₂ находились разные газы, то после удаления перегородки, даже при условии, что по обе стороны газы находятся под одинаковым давлении p_o, начнется необратимый самопроизвольный процесс диффузии, который приведет к выравниванию концентраций каждого из газов во всем объеме сосуда. Очевидно, что в процессе диффузии энтропия будет возрастать. Следовательно, в этом случае полное изменение энтропии системы больше значения, найденного ранее.

Чтобы рассчитать изменение энтропии в процессе диффузии, надо заменить реальный необратимый процесс таким воображаемым обратимым процессом, который приведет систему в то же самое конечное состояние. Такой процесс может быть осуществлен только с помощью полупроницаемых перегородок, т.е. перегородок, проницаемых для молекул одного газа и непроницаемых для молекул другого газа.

Ответ: ΔS=1,1 Дж/К.

63. Очень небольшой теплоизолированный сосуд разделен на две равные части теплопроницаемой перегородкой. В каждой части находится углекислый газ в количестве 10 моль. Температура газа в одной части сосуда t=28 ^oС, во второй части t=27 ^oС. Пренебрегая теплоемкостью сосуда, определить, во сколько раз возрастает вероятность системы при выравнивании температур? Определить изменение вероятности при переходе теплоты от менее нагретой части газа к более нагретой. Считать, что газ идеальный.

Решение. Согласно соотношению Больцмана, изменение энтропии прямо пропорционально натуральному логарифму вероятности w данного состояния системы:

S=S₂-S₁=kln(w₂/w₁).

Откуда

w₂/w₁=exp(S/k),

где k – постоянная Больцмана;

w – термодинамическая вероятность состояния – число, пропорциональное количеству тех физически различных микросостояний системы, которыми может быть реализовано данное макросостояние.

Для того чтобы найти изменение энтропии, следует рассмотреть квазистатический процесс, который может перевести систему из начального состояния в конечное. Поскольку объем газа, находящегося в каждой части сосуда, остается постоянным, таким процессом может быть квазистатическое изохорное нагревание одной части газа и квазистатическое изохорное охлаждение другой части. Причем каждый из этих процессов должен происходить в результате теплообмена с внешними термостатами при нарушении теплоизоляции системы.

Если температура газа, находящегося в первой части сосуда, изменяется от T₁ до T'₁, а во второй части – от T₂ до T'₂, то

,

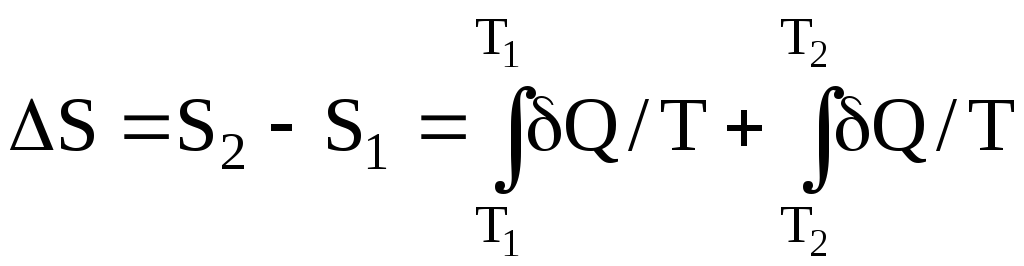где Q=mC_VdT/;

m/ – число молей;

C_V=iR/2 – молярная теплоемкость при постоянном объеме;

i=6 – число степеней свободы для углекислого газа.

Поскольку температура каждой части газа изменяется не в результате теплообмена с внешними термостатами, а в результате перехода теплоты от одной части газа к другой, то количество теплоты, отдаваемое одним газом, равно количеству теплоты, получаемому другим газом. (Теплоемкостью сосуда, а, следовательно, и количеством теплоты, им получаемым, можно пренебречь). Так как в обеих частях сосуда находится однородный газ одинаковой массы, то изменение температуры по модулю будет также одинаковым. Если в результате теплообмена температура газа в первой части сосуда уменьшится, так что T₁=T₁-T, то во второй части температура увеличится и T₂'=T₂+T. При выравнивании температур T₁'=T₂' имеем

T=(T₁-T₂)/2.

Подставив полученное соотношение в выражение для полного изменения энтропии, после интегрирования получим

S=mC_V/(ln(1-T/T₁)+ln(1+T/T₂)).

Поскольку T<<T₂, натуральные логарифмы можно разложить в степенной ряд и ограничиться только первыми членами. Тогда

S=mC_VT/(-1/T₁+1/T₂),

где mC_VT/=Q₁₂ – абсолютное значение количества теплоты, отданное одной и полученное второй частями газа. Следовательно, полученное выражение может быть использовано для расчета изменения энтропии не только при выравнивании температур, но при любом теплообмене между газами, находящимися в разных частях сосуда. В этом случае могут изменяться Q₁₂ и знак перед скобкой. Если Q₁₂ – количество теплоты, которое отдает менее нагретый, а получает более нагретый газ, то выражение, стоящие в скобках, полученного соотношения, примет вид (1/T₁-1/T₂).

В случае выравнивания температур, при T=0,5 К,

Q₁₂=1,2510^-7 Дж; S=1,3810^-12 Дж/К, а w₂/w₁=exp(10¹¹).

Изменение энтропии при переходе такого же количества теплоты от газа менее нагретого к газу более нагретому S'=-1,3810^-12 Дж/К и соответственно w₂'/w₁=1/exp10¹¹≈10^-48.

Полагая, что термодинамическая вероятность равна или прямопропорциональна числу случаев, когда данное состояние имеет место, полученный результат можно интерпретировать так: описанная в задаче система самопроизвольно переходит в состояние, при котором температуры газов будут равны практически всегда; переход теплоты от менее нагретого газа к более нагретому невозможен.

Однако если рассматривать вероятность перехода количества теплоты на много порядков меньше, например Q₁₂=1,2510^-17 Дж, то в этом случае изменение энтропии при передаче теплоты от более нагретого газа к менее нагретому S=1,3810^-22 Дж/К и w₂'/w₁=е¹⁰≈210⁴.

Изменение энтропии при переходе этого же количества теплоты от менее нагретого газа к более нагретому S'=-1,3810^-22 Дж/К и w'₂/w₁=e^-10=0,510⁴. Это значит, что уже в одном случае из 210⁴ возможен процесс перехода теплоты от менее нагретого газа к более нагретому, т.е. вероятность такого процесса резко повышается.

Очевидно, для того чтобы передача такого количества теплоты (порядка 10^-17 Дж) могла хоть изменить температуру газа, количество газа должно быть резко уменьшено. Так, для изменения температуры на 0,01 К число молей газа должно составлять 10^-15÷10^-16, что соответствует общему количеству молекул N=10⁸÷10⁷. Для макроскопических объемов, содержащих такое количество молекул, уже можно говорить о реальной вероятности процесса, идущего в нарушение второго начала термодинамики.

64. В баллоне вместимостью V=8 л находится кислород массой m=0,3 кг при температуре T=300К. Найти, какую часть вместимости сосуда составляет собственный объем молекул газа? Определить отношение внутреннего давления p' к давлению p газа на стенки сосуда.

Решение. Для получения ответа на первый вопрос задачи необходимо найти отношение

k=V'/V,

где V' – собственный объем молекул.

Собственный объем молекул найдем, воспользовавшись постоянной Ван дер Ваальса b, равной учетверенному объему молекул, содержащихся в одном моле реального газа. В уравнении Ван дер Ваальса:

поправка b означает учетверенный объем молекул всего газа, т.е.

b=4V'.

Отсюда

V'=b/4, или V'=mb/(4),

где =m/ – количество вещества;

 – молярная масса.

Подставив полученное значение V' в формулу для определения k, найдем:

Для ответа на второй вопрос задачи надо найти отношение

k=p'/p.

Как следует из уравнения Ван дер Ваальса

или

где a – постоянная Ван дер Ваальса для одного моля газа.

Давление p, производимое газом на стенки сосуда, найдем из уравнения Ван дер Ваальса

Проверив размерности полученных результатов, подставив численные значения в СИ, будем иметь:

k=0,91.

Это означает, что собственный объем молекул составляет 0,91 от объема сосуда;

p'=179 кПа; p=2,8410⁶ Па; k₁=6,3%.

Следовательно, давление газа, обусловленное силами притяжения молекул, составляет 6,3% давления газа на стенки сосуда.

Ответ: k=0,91; p'=179 кПа; p=2,8410⁶ Па; k₁=6,3%.

65. Углекислый газ, содержащий =1 моль вещества, находится в критическом состоянии. При изобарном нагревании газа его объем V увеличился в k=2 раза. Определить изменение ΔT температуры газа, если его критическая температура Т_кр=304К.

Решение. Для решения задачи удобно воспользоваться уравнением Ван дер Ваальса в приведенной форме, т.е. в такой форме, когда давление p, молярный объем V_m и температура T реального газа с соответствующими критическими параметрами представлены в виде следующих соотношений:

.

Из этих выражений получим:

; .

Подставив сюда выражения p_кр, V_mкр, и T_кр через постоянные Ван дер Ваальса a и b, найдем:

p=a/27b²; V_m=3b; T=8a/27bR.

Полученные выражения p, V_m и T подставим в обычное уравнение Ван дер Ваальса:

.

После сокращений на a/27b и в правой части на R получим

Полученное соотношение является уравнением Ван дер Ваальса в приведенной форме. Оно не содержит никаких параметров, характеризующих индивидуальные свойства газа, и поэтому является универсальным.

Так как давление остается постоянным (p=p_кр), то =1; молярный объем газа согласно условию задачи увеличился в два раза, т.е. V_m=2V_mкр, следовательно, =2.

Из уравнения выразим приведенную температуру:

Подставив сюда значения и произведя вычисления, найдем

=35/32.

Температура T , как отмечалось, связана с приведенной температурой  и критической T_кр соотношением T=T_кр. Произведя вычисление по этой формуле, получим

T=35/32304=322 К.

Ответ: T=322 К.

66. В цилиндре под поршнем находится хлор массой m=20 г. Определить изменение ΔU внутренней энергии хлора при изотермическом расширении его от V₁=200 см³ до V₂=500 см³.

Решение. Внутренняя энергия U реального (вандерваальсового) газа определяется выражением

Выразив в этом выражении молярный объем V_m через объем V и количество вещества  (V_m=V/) и учтя, что =m/, получим

Изменение внутренней энергии в результате изотермического расширения найдем как разность двух значений внутренней энергии при объемах V₂ и V₁:

Подставив значения величин в СИ и произведя вычисление, получим

Заметим, что для идеального газа такое изменение внутренней энергии соответствовало бы нагреванию на 26,3К.

Ответ: ΔU=154 Дж.

67. В очень прочном стальном баллоне заключена вода, занимающая при комнатной температуре половину объема баллона. Найти давление (в технических атмосферах) и плотность водяных паров при повышении температуры до 400^oС.

Решение. Из таблицы критических температур возьмем для воды t=374^oС. Таким образом, при нагревании воды в баллоне до 400^oС она оказалась при температуре выше критической. Следовательно, она вся будет находится в газообразном, или, как это принято говорить в отношении воды, парообразном состоянии.

Плотность водяного пара определим, учитывая, что объем одной и той же массы воды в результате ее нагревания увеличился в два раза (массу паров, находящихся над водой при комнатной температуре, можно не учитывать). Следовательно, плотность пара, равная отношению массы к объему, будет вдвое меньше плотности воды _В=110³ кг/м³:

=_В/2=510² кг/м³.

Так как плотность пара в баллоне оказалась большой по сравнению с плотностями газов при нормальных условиях (например, плотность воздуха при нормальных условиях равна 1,29 кг/м³), то, очевидно, водяной пар здесь можно рассматривать как реальный газ, параметры которого связаны уравнением состояния Ван дер Ваальса:

.

Решив его относительно p, получим

Здесь V_o – молярный объем, но не объем всей массы пара. Поэтому на основании определения плотности можно записать

V_o=/,

где  – молярная масса пара.

Подставив это значение V_o в вышенаписанную формулу, найдем

Взяв из таблиц значения постоянных a и b для воды, выразив все величины, входящие в формулу, в единицах СИ, выполнив вычисления, найдем

p=5,110⁸ Па=5,210³ ат.

Ответ: p=5,210³ ат.

68. Определить давление m=280 г азота, находящегося при температуре 27 ^oС в сосуде, объем которого равен: 1) V=1,00 м³;

2) V=0,50 л.

Решение. Чтобы решить вопрос о том, каким следует считать данный газ – идеальным или реальным, найдем молярный объем газа V_o. Пусть в сосуде содержится =m/ молей газа. Тогда

V_o=V/=V/m.

Учитывая, что молярная масса азота =0,028 кг/моль, получим:

1) Vo=1,000,28/0,28=0,10 м³/моль;

2) Vo=0,510^-30,028/0,28=5,010^-5 м³/моль.

Сравнивая вычисленные значения V_o с молярным объемом газа при нормальных условиях V_o(норм)=22,410^-3 м³/моль, видим, что в первом случае газ достаточно разряжен и его можно считать идеальным. Уравнение состояния идеального газа для одного моля запишем так:

Отсюда

Во втором случае V_o<V_o(норм), и газ следует считать реальным. Его давление найдем из уравнения Ван дер Ваальса для реального газа

Взяв из таблиц значения постоянных Ван дер Ваальса для азота: a=0,13 м⁴Н/моль², b=3,710^-5 м³/моль, произведем вычисление:

p=1,410⁸ Па.

Заметим, что, вычисляя давление по формуле, характерной для состояния идеального газа, получили бы в этом случае неверный результат:

p=0,510⁸ Па.

Ответ: p=0,510⁸ Па.

69. Определить массу кислорода в баллоне, объем которого V=10,0 л при температуре 27 ^oС и давлениях:1) p₁=1,00 ат; 2) p₂=410 ат.

Решение. В первом случае (p=1,00 ат) кислород в баллоне находится при условиях, близких к нормальным. То обстоятельство, что температура газа несколько выше нормальной, означает лишь, что его плотность при этом давлении меньше, чем при нормальных условиях. Поэтому без большой погрешности можно считать газ идеальным. На основании уравнения состояния идеального газа, учитывая, что для кислорода =0,032 кг/моль, получим:

кг.

Во втором случае (p=410 ат), учитывая большое по сравнению с нормальным давление газа, следует считать его реальным и вести расчеты на основании уравнения Ван дер Ваальса.

Масса газа определяется соотношением:

,

где  – молярная масса;

 – число молей;

V – объем газа;

V_o – его молярный объем.

Таким образом, необходимо из уравнения Ван дер Ваальса

,

найти величину V_o, а затем массу газа.

Уравнение Ван дер Ваальса является уравнением третьей степени относительно V₀ и поэтому имеет, вообще говоря, три корня. Однако учитывая, что кислород в баллоне находится при температуре выше критической (t_кр=-119 ^oС), можно утверждать, что при определенном давлении газ будет иметь лишь один определенный объем. Следовательно, кубическое относительно V_o уравнение Ван дер Ваальса имеет в данном случае лишь один действительный корень. Его можно найти методом последовательных приближений, поскольку расчеты, связанные с решением кубического уравнения по общей формуле Кардано, весьма громоздки.

В качестве первого приближения вычислим молярный объем V_o1 газа, рассматривая его как идеальный. Тогда из уравнения состояния идеального газа получим

Теперь, обозначив в уравнении Ван дер Ваальса поправку на давление через p_o1=a/V_o², найдем величину V_o

Взяв из таблиц значения постоянных a и b для кислорода, выразим в единицах СИ входящие в формулу величины: p=4109,810⁴ Па, V_o1=0,6210^-4 м3/моль, R=8,3 Дж/(мольК), Т=300 К, a=0,13 м⁴Н/моль², b=3,110^-5 м³/моль. Выполнив вычисление, найдем

V_o2=0,6510^-4 м³/моль.

Еще раз, вычислив по формуле, полученной из уравнения Ван дер Ваальса, считая при этом p₁=a/V_o2², получим третье приближение:

V_o3=0,6610^-4 м³/моль.

Повторяя таким образом вычисления, будем получать все более точные значения V_o:

V_o4=0,6710^-4 м³/моль; V_o5=0,6710^-4 м³/моль;

Видим, что при дальнейших вычислениях, если ограничиться точностью до второго знака, результат не будет изменяться. Если же взять значение V_o5=0,6810^-4 м³/моль, то получим прежнее значение

V_o6=0,6710^-4 м³/моль.

Поэтому, действительным корнем кубического уравнения Ван дер Ваальса, вычисленным с точностью до второго знака, будет

V_o=0,6710^-4 м³/моль.

Теперь вычислим искомую массу газа

кг.

Легко убедиться в том, что вычисление по уравнению Менделеева-Клапейрона дало бы в этом случае неверный результат

кг.

Ответ: 1). m=0,013 кг; 2). m=4,8 кг.

70. Какую часть объема стеклянной ампулы должен занимать жидкий эфир при t=20 ^oС, чтобы при его нагревании можно было наблюдать переход вещества через критическое состояние? Для эфира =0,074 кг/моль, =714 кг/м³ при 20 ^oС, t=194 ^oС, p=35,6 ат.

Решение. Переход вещества через критическое состояние характерен тем, что при этом исчезает различие между жидкой и газообразной фазами вещества. Критическое состояние характеризуется определенными для каждого вещества параметрами: критическими значениями температуры Т_к, давления p_к и молярного объема V_0к. При этом критический объем всей массы вещества, содержащей =m/ молей, равен:

V_к= V_0к=(m/) V_0к.

Если вещество, нагретое до критической температуры T_к, окажется в объеме V, не равном V_к,то оно не будет при этом находиться в критическом состоянии. В этом случае при достижении температуры T_к не будет исчезать различие между двумя фазами, так как еще до достижения T_к все вещество при нагревании постепенно перейдет в одну фазу (при V>V_к вся жидкость в сосуде испарится, при V<V_к весь пар сконденсируется). Таким образом, для того чтобы наблюдать переход вещества, находящегося в ампуле, через критическое состояние, необходимо, чтобы при достижении критической температуры занимаемый им объем V был равен критическому объему V_к.

Так как в этот момент вещество будет равномерно заполнять всю ампулу, то V является одновременно и объемом ампулы.

Искомое отношение объема V_ж жидкого эфира к объему V ампулы найдем из ранее написанных уравнений, с учетом того, что m/V_ж= – плотность жидкого эфира:

V_ж/V=V_ж/V_к=V_ж/mV_0к=/V_oк.

Выразив величину V_0к через известные p_к и T_к получим

T_к/p_к=8a27b²/27bRa=8b/R; V_0к=3b=3RT_к/8p_к.

Окончательно для искомого отношения имеем:

V_ж/V=8p_к/(3RT_к).

Выразим в единицах СИ данные величины: =0,074 кг/моль, p=35,69,810⁴ Па, =714 кг/м³, Т_к=467 К. Подставив эти значения в формулу и выполнив вычисление, найдем

V_ж/V=0,25.

Ответ: V_ж/V=0,25.

71. Какой толщины следовало бы сделать деревянную стену здания, чтобы она давала такую же потерю теплоты, как и кирпичная стена толщиной d=40 см при одинаковой температуре внутри и снаружи здания? Коэффициенты теплопроводности кирпича и дерева равны соответственно: К_к=0,70 Вт/(мК), К_д=0,175 ВТ/(мК).

Решение. Количество теплоты, переданное через площадь S за время , если расстояние между плоскостями d, а разность температур между ними T, равно

Q=KTS/d,

где K – коэффициент теплопроводности.

Запишем уравнение теплопроводности через стену для обеих материалов:

Так как потеря теплоты должна быть одинаковое, т.е. Q_к=Q_д, имеем

.

Откуда толщина деревянной стены

d_д=d_кK_д/K_к.

Подставим в полученное соотношение числовые значения в единицах СИ, после вычислений, будем иметь

d_д=0,40,175/0,70=0,1 м.

Ответ: d_д=0,1 м.

72. Стена нагревательной печи толщиной d=0,75 м выполнена целиком из огнеупорного шамотного кирпича с коэффициентом теплопроводности K₁=1 Вт/(мК). Какова будет толщина стены, если ее выполнить двухслойной, сохранив первый слой из того же материала толщиной d₁=0,25 м, а второй слой из неогнеупорного, но малотеплопроводного, материала, у которого коэффициент теплопроводности K₂=0,1 Вт/(м К)? Тепловой поток и температуры наружных поверхностей у двухслойной стены те же, что и у однослойной.

Решение. Тепловой поток – количество теплоты, переданное единичной площади в единицу времени, можно определить по формуле

где K – коэффициент теплопроводности;

T – разность температур;

d – расстояние между двумя плоскостями.

Запишем уравнение теплового потока через однослойную стену и через каждый из слоев двухслойной:

q₁=K₁(t₁-t₃)/d, q₂=K₁(t₁-t₂)/d₁, q₃=K₂(t2-t₃)/d₂.

Из каждого соотношения выразим изменение температур

(t₁-t₃)=qd/K₁, (t₁–t₂)=qd₁/K₁, (t₂-t₃)=qd₂/K₂.

Складывая левые и правые части вышенаписанных формул, получим

2(t₁-t₃)=q(d/K₁+d₁/K₁+d₂/K₂).

Подставим в последнее выражение значение q для однослойной стены и, преобразовав, имеем

d₂₌K₂(d-d₁)/K₁.

Тогда общая толщина двухслойной стены будет равна:

d₃=d₁+d₂=d₁+K₂(d-d₁)/K₁.

Подставив значения величин в единицах СИ, произведем вычисление

d₃=0,3 м.

Ответ: d₃=0,3 м.

73. Определить время подъема движущихся с постоянной скоростью пузырьков воздуха со дна водоема глубиной ℓ=1 м (рис. 3.15), если диаметры пузырьков соответственно равны 2 мм и 1 мм.

Решение. В рассматриваемом случае уравнение движения пузырьков имеет вид

ma=F+F_A+F_с,

где m – масса пузырька;

a – его ускорение;

F=mg – сила тяжести;

F_A – подъемная сила (сила Архимеда);

F_c – сила сопротивления (внутреннего трения).

Так как движение пузырька равномерное, то, очевидно, сила сопротивления движению уравновешивается подъемной силой; силой тяжести можно пренебречь, так как плотность воздуха во много раз меньше плотности воды. Предполагая, что пузырек имеет небольшой радиус и сферическую форму, то согласно закону Стокса, силу сопротивления движению можно определить по формуле:

F_с=6r,

где  – коэффициент вязкости;

r – радиус пузырька;

v – его скорость.

Подъемая сила

F_A=_ogV=4r³_og/3,

где _o – плотность воды;

g – ускорение силы тяжести.

Таким образом:

6rv=4r_og/3,

или

6rℓ/t=4r_or³g/3,

где ℓ – путь, проходимый пузырьком;

t – время его движения.

Из последнего соотношения находим время движения пузырька

t=9ℓ/(2r²_og).

Подставив значения величин в единицах СИ, получим

t₁=0,505 с; t₂=2,02 с.

Ответ: t₁=0,505 с; t₂=2,02 с.

74. Чему равны при нормальных условиях коэффициенты диффузии и внутреннего трения азота, если эффективный диаметр молекулы азота d=3,110^-10 м?

Решение. Из молекулярно кинетических представлений можно показать, что коэффициенты внутреннего трения и диффузии определяется соотношениями

;

,

где <v> – средняя арифметическая скорость молекул;

<λ> – их средняя длина свободного пробега;

ρ – плотность газа.

Средняя арифметическая скорость

,

где R – универсальная газовая постоянная;

Т – его абсолютная температура;

μ – молярная масса газа.

Средняя длина свободного пробега

,

где k – постоянная Больцмана;

d – эффективный диаметр молекулы;

p – давление газа.

Плотность газа можно определить воспользовавшись уравнением Менделеева-Клапейрона

.

Подставив величины, входящие в вышенаписанные формулы в единицах СИ <v>=457 м/с; <λ>=8,7210^-8 м, ρ=1,25 кг/м³, получим

η=16,610^-6 кг/(мс); D=1,3610^-5 м²/с.

Ответ: η=16,610^-6 кг/(мс); D=1,3610^-5 м²/с.