В случае переменной массы

,

где – реактивная сила.

При движении по кривой результирующая сила может быть разложена на две составляющие (рис. П 1. 13)

; ,

где R – радиус кривизны траектории;

– тангенциальная составляющая (касательная сила)

– нормальная составляющая (центростремительная сила).

Основной закон классической динамики – инвариантен при переходе от одной инерциальной системы к другой, при этом

ma=F; ma^'=F^'; F=F^'.

Третий закон классической динамики – силы, с которыми взаимодействуют два тела, равны по величине и противоположны по направлению. Силы действия и противодействия приложены к разным телам и никогда не уравновешивают друг друга (рис. П 1. 14):

F₁₂= -F₂₁.

Импульс силы – мера действия силы за некоторый промежуток времени:

.

Силы инерции. Обусловлены ускоренным движением системы отсчета по отношению к неподвижной системе. Различают:

1) силы, действующие на тело при ускоренном поступательном движении системы отсчета (рис. П 1. 15):

ma^’= ma+F_ин,

где a^’ – ускорение тела в неинерциальной системе отсчета;

a – ускорение тела в инерциальной системе отсчета;

F_ин – сила инерции.

2) силы, действующие на тело, покоящееся во вращающейся системе отсчета (рис. П 1. 16):

,

где F_ц – центробежная сила инерции;

 – угловая скорость вращающейся системы отсчета;

r^’ – радиус – вектор тела относительно начала вращающейся системы отсчета;

R – перпендикулярная к оси вращения составляющая r^’.

3) силы, действующие на тело, движущееся во вращающейся системе отсчета (рис. П 1. 17):

F_к=2m[v^’ ω],

где F_к – сила Кориолиса;

v^’ – скорость движения тела;

 – угловая скорость вращающейся системы отсчета.

Основной закон динамики для неинерциальных систем отсчета:

ma^’=F+F_ин+F_ц +F_к,

где F, F_ин, F_ц, F_к – ранее рассмотренные силы, действующие в неинерциальных системах отсчета.

Основная задача динамики вращательного движения – нахождение угловых ускорений, сообщаемых известными силами.

Момент инерции – скалярная физическая величина, характеризующая инертность тела при вращательном движении.

Момент инерции материальной точки относительно неподвижной оси вращения – физическая величина, равная произведению массы материальной точки на квадрат расстояния до оси или центра вращения (рис. П 1. 18):

I=mr².

Момент инерции тела относительно оси z – физическая величина, равная сумме моментов инерции отдельных материальных точек тела относительно той же оси вращения (рис. П 1. 19):

; ,

где m_i – масса i – й точки;

r_i – расстояние i – й точки до оси z;

ρ – плотность вещества, из которого состоит тело;

V – объем тела.

Теорема Штейнера – момент инерции тела относительно произвольной оси z равен сумме момента инерции того же тела I₀ относительно оси, параллельной данной и проходящей через центр масс, и произведения массы тела m на квадрат расстояния между осями (а):

I_z=I₀+mа².

На рисунке П 1. 20 представлено применение теоремы Штейнера к расчету момента инерции диска относительно оси ОО^' параллельной оси О₁О₁^'.

Главные оси инерции – три взаимно перпендикулярных свободных оси вращения тела произвольной формы, проходящие через его центр масс.

Момент импульса материальной точки относительно неподвижной оси вращения (L) – векторная физическая величина, модуль которой равен произведению модуля импульса на плечо (рис. П 1. 21):

L=p.

В векторной форме

L=[rp]=[rmv],

где m – масса материальной точки;

v – скорость материальной точки;

 – плечо (кратчайшее расстояние от направления импульса до оси вращения).

Момент импульса системы относительно неподвижной оси вращения z – проекция на эту ось вектора L (момента импульса системы):

,

где r_i, p_i – радиус – вектор и импульс i – й материальной точки;

n – общее число точек в системе.

Связь момента импульса тела с вектором угловой скорости ω и моментом инерции:

L=Iω.

Момент силы относительно центра вращения или неподвижной оси вращения – векторная физическая величина, модуль которой равен произведению модуля силы на плечо (рис. П 1. 22):

M=F,

где  – плечо силы – кратчайшее расстояние от линии действия силы до центра вращения.

В векторной форме

M=[rF].

Главный или результирующий момент сил относительно неподвижной оси вращения равен векторной сумме моментов слагаемых сил:

.

Моменты сил относительно осей, которые перпендикулярны и параллельны оси вращения, равны нулю.

Основной закон динамики вращательного движения твердых (недеформирующихся) тел, для которых I=const (второй закон динамики для вращательного движения):

M=I∙ε; .

Импульс вращающего момента – произведение вращающего момента на время его действия:

Mdt=dL.

Осциллятор – физическая система, совершающая колебания. Система, у которой величины, описывающие ее, периодически меняются с течением времени.

Гармонический осциллятор – механическая система, совершающая колебания около положения устойчивого равновесия, описывающие величины, которой изменяются по гармоническому закону (закону синуса или косинуса).

Уравнение движения гармонического осциллятора:

; ; ,

где a=d²x/dt²= -ω₀²x – ускорение материальной точки;

F – возвращающая сила, которая стремится вернуть систему в положение равновесия (F= -mω₀²x= -kx);

x – смещение;

k=mω₀² – коэффициент возвращающей силы. Он численно равен возвращающей силе, вызывающей единичное смещение.

Решение уравнения движения гармонического осциллятора:

x=x₀sin(ω₀t+φ₀).

Уравнение гармонических колебаний в комплексном виде:

.

В теории колебаний принимается, что величина «x« равна вещественной части комплексного выражения, стоящего в этом выражении справа.

Дифференциальное уравнение гармонического колебательного движения

.

Решением дифференциального уравнения гармонических колебаний является выражение вида

x=x₀ sin(₀t+₀),

где k=m₀² – коэффициент возвращающей силы;

x – смещение материальной точки;

x_o – амплитуда колебаний;

_o=2/Т=2 – круговая (циклическая частота);

= 1/T – частота колебаний;

T – период колебаний;

= (₀t+₀) – фаза колебаний;

₀ – начальная фаза колебаний.

Примеры гармонических осцилляторов: пружинный, физический, и математический маятники:

а) пружинный маятник – тело массой m (рис. П 1. 23), подвешенное на пружине, совершающее гармоническое колебание.

Упругие колебания совершаются под действием упругих сил

F= -k∙,

где k=m_o² – коэффициент жесткости;

 – относительное удлинение.

Уравнение движения пружинного маятника:

; ,

где ;

 – величина деформации.

Решение уравнения движения пружинного маятника:

=( )₀sin(ω₀t+φ₀).

Круговая частота, частота и период колебаний пружинного маятника:

; ;;

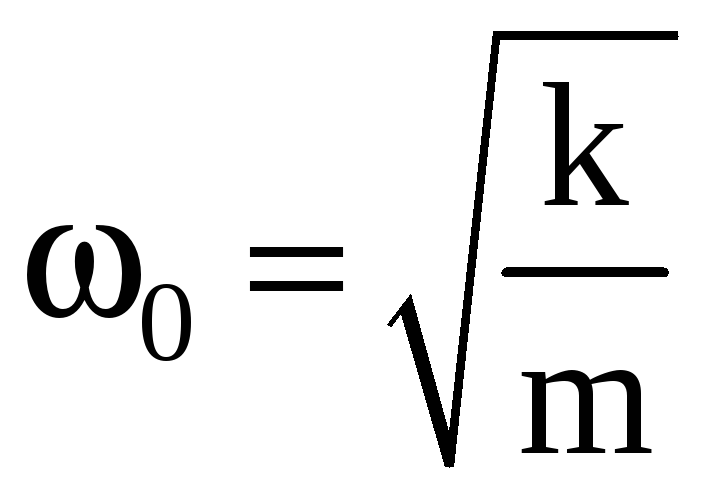б) физический маятник – твердое тело, совершающее гармоническое колебательное движение относительно оси, не совпадающей с центром масс (рис. П 1. 24).

Уравнение движения физического маятника:

.

Решение уравнения движения физического маятника:

=₀sin(ω₀t+α),

где α – начальная фаза колебаний.

Круговая частота, частота и период колебаний физического маятника:

; ; ; ,

где L=I/md – приведенная длина физического маятника – длина такого математического маятник, период колебаний которого равен периоду колебаний физического маятника;

I – момент инерции физического маятникa относительно оси колебаний;

m – масса физического маятника;

d – расстояние между осью колебаний и центром масс.

в) математический маятник – тело массой m, размерами которого можно пренебречь, подвешенное на невесомой, нерастяжимой нити (рис. П 1. 25).

Круговая частота, частота и период колебаний математического маятника:

; ; .

Приведенная длина физического маятника – величина, численно равная длине такого математического маятника, период колебаний которого равен периоду колебаний физического маятника:

.

Крутильные колебания – колебания, совершающиеся под действием закручивающего момента, пропорционального углу закручивания (колебания диска, подвешенного на стальной нити):

M= – D,

где – коэффициент крутильной жесткости;

G – модуль сдвига;

r – радиус нити;

 – длина нити.

Период колебаний крутильного маятника

,

где I _z – момент инерции тела относительно оси колебаний.

Затухающие (свободные) колебания – движения реальной колебательной системы, сопровождающиеся силами трения и сопротивления, которые приводят к уменьшению амплитуды колебаний (рис. П 1. 26). При этом энергия, потерянная системой, не восполняется за счет внешних сил.

Дифференциальное уравнение затухающих колебаний:

,

где r – коэффициент сопротивления.

Решение уравнения затухающих колебаний:

,

где А=x₀e ^{– βt} – амплитуда колебаний, убывающая по экспоненциальному закону;

β=r/(2m) – коэффициент затухания, характеризующий быстроту убывания амплитуды с течением времени;

– собственная частота колебаний системы, т.е. та частота, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды (r=0).

Круговая частота, частота и период затухающих колебаний:

; ; .

Характеристики затухающих колебаний:

1) декремент затухания – отношение двух смещений, отличающихся друг от друга по времени на период. Декремент затухания характеризует быстроту затухания в зависимости от числа колебаний:

.

2) логарифмический декремент затухания – величина, равная натуральному логарифму от декремента затухания. Логарифмический декремент затухания характеризует затухание колебаний за период:

=lnD=ln(e^βΤ)=βT.

Добротность колебательной системы

,

где N_e – число колебаний, за то время, за которое амплитуда колебаний уменьшается в «е» раз.

Вынужденные колебания – колебания, совершаемые системами под действием внешней (вынуждающей) силы, изменяющейся по какому – либо закону, например гармоническому (рис. 27):

f=F₀cost,

где F₀ – амплитудное значение вынуждающей силы;

 – частота вынуждающей силы.

Дифференциальное уравнение вынужденных колебаний:

,

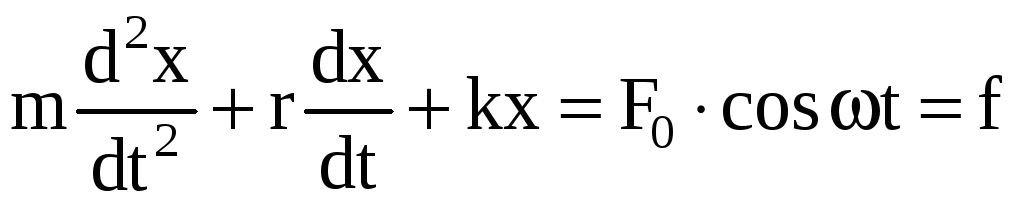где f=F₀ sint – вынуждающая сила;

 – частота вынуждающей силы.

Решение уравнения вынужденных колебаний:

X=X₁+X₂=x₀e ^{– t}sin(ω't+φ₀')+x₀sin(ωt+φ),

где .

Амплитуда и начальная фаза вынужденных колебаний:

;

.

Резонанс – явление резкого возрастания амплитуды колебаний при некоторой определенной для данной колебательной системы частоте (резонансной частоте). На рисунке 28 показаны возможные кривые при резонансе.

Резонансная частота

.