Потенциальная энергия растянутого (сжатого) стержня- это энергия упругой деформации!

Так как в законе Гука ( ), в данном случае =; =,  ,  .

Поскольку Sl – объем стержня длины l, то плотность потенциальной энергии (энергия единицы объема) равна

. (41)

При прохождении продольной волны каждая единица его объема обладает еще и кинетической энергией, плотность которой, очевидно, равна половине произведения плотности на квадрат скорости удлинения, поэтому плотность полной энергии равна сумме

. (42)

Выразим модуль Юнга через скорость из (34)(42), тогда

. (43)

Продифференцировав уравнение волны (23) по времени и по координате, легко (?!) убедиться, что оба слагаемых равны друг другу, 

Плотности кинетической и упругой (потенциальной) энергии в этой волне одинаковы и изменяются синхфазно!

В частности, плотность энергии волны можно выразить как . Тогда для гармонической волны (x,t)=аcos(t-kx) плотность энергии равна

w=а²² sin² (t-kx) . (44)

Среднее значение плотности энергии за период (или за t>>T) равно

(45)

поскольку среднее значение квадрата синуса за период равно ½. Полученное выражение справедливо также и для упругих волн в жидкостях и газах.

Плотность потока энергии. Вектор Умова. Потоком энергии Ф называется количество энергии переносимое волной через поверхность S в единицу времени . Поток энергии в разных точках поверхности S может быть разным. Чтобы более детально охарактеризовать это обстоятельство вводят понятие плотности потока энергии: это поток энергии через единичную площадку, перпендикулярную к направлению переноса энергии: . Если φ – угол между нормалью к dS и направлением переноса энергии (совпадающим с), то

энергию dW(=wdV), переносимую через dS за время dt можно выразить через скорость и w:

dW= w dt dScosφ, , . И поскольку направление совпадает с направлением переноса энергии, то аналогично можно записать и вектор плотности потока энергии (вектор Умова):

. (46)

Из выражения (46) видно, что величина вектора плотности потока энергии пропорциональна w, среднее по времени значение которой определяется формулой (45), поэтому и среднее значение вектора

. (47)

Интенсивность волны – это I=, т.е. модуль среднего по времени вектора плотности потока энергии – модуль среднего вектора Умова.

Интенсивность пропорциональна квадрату амплитуды и квадрату частоты волны.

Связь между вектором и полным потоком Ф через произвольную поверхность S очевидна

. (48)

Стоячие волны. Опыт показывает, что при одновременном прохождении в среде нескольких волн колебания частиц среды оказываются векторной суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. В этом состоит принцип суперпозиции (наложения) волн. Рассмотрим практически важный случай, когда две гармонические волны ₁ и ₂ с одинаковыми частотами и амплитудами распространяются в противоположных направлениях оси х:

; ;

где для простоты начальные фазы выбраны равными нулю. Суперпозиция этих волн дает

, (49)

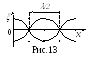-это и есть уравнение стоячей волны. Если рассматривать |2аcoskx| как амплитуду, то выражение (49) представляет собой колебание с частотой  и амплитудой, зависящей от координаты (рис.13). Такое явление называется стоячая волна (в отличие от ранее рассмотренных – бегущих волн). В точках, где 1 находятся максимумы, которые для стоячей волны называются пучностями; а при =0 – узлы. Период функции , поэтому интервал между соседними узлами или пучностями равен половине длины волны /2. Между двумя соседними узлами все точки колеблются синхфазно, но при переходе через узел фаза меняется на , поэтому колебания по разные стороны от узла происходят в противофазе. Таким образом, узлы делят среду на независимые области длиной /2, в которых происходят независимые и никуда не распространяющиеся колебания. Никакой передачи энергии через узлы не происходит, нет распространения возмущения вдоль оси х. Стоячие волны в большей степени являются колебаниями, чем собственно волнами.

Продифференцировав (49) по времени, найдем скорость частиц среды , а продифференцировав по координате – относительную деформацию :

; . (50)

Следовательно, скорость и деформация тоже являются стоячими волнами, сдвинутыми относительно друг друга по фазе на как в пространстве, так и во времени. Поскольку кинетическая энергия ведет себя как квадрат скорости, а потенциальная – как квадрат смещения, то соответственно происходят и превращения энергии стоячей волны: то полностью в потенциальную (упругую), то полностью в кинетическую. При этом в момент максимального смещения наиболее растянуты области узлов,  там запасена потенциальная энергия; в момент нулевого смещения максимальная скорость в пучностях,  там максимальна кинетическая энергия. Таким образом, внутри области размером /2 происходят превращения потенциальной энергии в кинетическую и наоборот, соответственно передача энергии от узлов к пучностям и наоборот. При этом никакого переноса энергии через узлы и ее распространения не происходит. Величина среднего потока энергии через любую плоскость, перпендикулярную оси х равна нулю.

Колебания струны, закрепленной с обоих концов. При возбуждении в струне поперечного возмущения, в ней могут возникнуть стоячие волны, но не любой частоты. Это связано с очевидными граничными условиями: на концах струны должны быть узлы. Отсюда следует, что на струне длиной l должно укладываться целое число полуволн:. Это значит, что могут быть возбуждены колебания с длинами волн, подчиняющимися условию , или частот , где n=1,2,3…; а фазовая скорость (см. 36) зависит от силы, приложенной к струне (сила натяжения), и линейной плотности материала струны.

Частоты, определяемые по формуле

(51)

называются собственными частотами струны; частоту ₁ (n=1) называют основной частотой, остальные частоты (n=2,3,…) – обертонами. Гармонические колебания с частотами (51) называются собственными колебаниями, или гармониками.

Звуковые волны. Так называется распространяющийся в упругой среде волновой процесс (в диапазоне от 20 Гц до 20 кГц), воспринимаемый человеческим ухом. Упругие волны с частотой меньше 20 Гц называются инфразвуком, больше 20 кГц – ультразвуком. Звук различают по высоте, тембру и громкости. Высота звука определяется его частотой: чем больше , тем выше звук. Тембр звука определяется всем набором частот этого звука, который называется его акустическим спектром. Этот спектр может состоять из непрерывного или дискретного набора частот. Именно тембром определяются отличия в звучании музыкальных инструментов.

Громкость звука – это мера слухового ощущения, качественно характеризуемая терминами от тихого до громкого. При неизменной частоте громкость звука растет с увеличением его интенсивности I (Вт/м²). Минимальная величина I10^-12 Вт/м² (порог слышимости). При интенсивности звука I10 Вт/м² (порог болевого ощущения) восприятие звука сменяется ощущением давления и боли. Оба порога зависят от частоты колебаний. Субъективное восприятие громкости возрастает значительно медленнее роста интенсивности звука, поэтому используют логарифмическую шкалу, в которой громкость звука оценивают величиной L:

, где L_Б – уровень интенсивности звука в белах (Б), I₀  10^-12 Вт/м² – порог слышимости при частоте 1 кГц. Таким образом, уровень порога слышимости L_Б=0. Обычно пользуются не белами, а в 10 раз меньшей единицей – децибелом:

. (52)

В этих же единицах можно измерять уменьшение (затухание) интенсивности звука на расстоянии. Например, затухание в 20 дБ соответствует уменьшению интенсивности в 100 раз. Действительно: , где - интенсивность в точке, расположенной ближе к источнику.

Эффект Доплера для звуковых волн. Если источник звука, или приемник, или они оба движутся относительно среды, то частота , воспринимаемая приемником отличается от частоты, испускаемой источником . Это явление называется эффектом Доплера, и объясняется уплотнением (разряжением) импульсов, обусловленным движением источника и приемника. Опуская вывод, приведем формулу, связывающую частоты источника  и приемника  :

, (53)

где и - проекции скоростей источника и приемника на ось х, направленную от источника к приемнику,  - скорость звуковых волн в данной среде.