Лабораторная работа № 19 основное уравнение динамики вращательного движения вокруг неподвижной оси

Цель работы:

Изучение динамики вращательного движения твердого тела. Исследование зависимости угла поворота твердого тела от времени, экспериментальная проверка основного уравнения динамики вращательного движения, определение момента инерции твердого тела как коэффициента пропорциональности в основном уравнении.

Оборудование:

Установка, включающая исследуемый диск с закрепленными на нем шкивами, грузы известной массы, датчик угла поворота (световой барьер), электронный блок управления Cobra 3, турбокомпрессор, компьютер.

Продолжительность работы – 4 часа.

Теоретическая часть

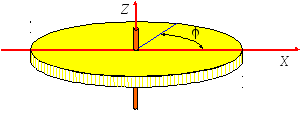
1. Рассмотрим диск, который может вращаться вокруг неподвижной оси Z. Положение диска определяется углом , который составляет радиальная прямая, связанная с диском (например, нарисованная на диске), с осью X, неподвижной относительно лабораторной системы отсчета (рис. 1).

Рис. 1. Положение диска характеризуется угловой координатой

Вращение диска характеризуется скоростью , и угловым ускорением . Аналогичным образом можно ввести угловую координату, угловую скорость и угловое ускорение для произвольного твердого тела, вращающегося вокруг неподвижной оси.

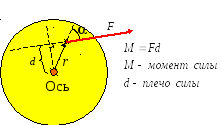
2. Угловое ускорение диска зависит не только от величины и направления действующей на него силы, но и от положения точки, к которой эта сила приложена. «Вращательное действие» силы характеризуется моментом силы относительно оси, который равен произведению модуля силы на плечо силы - так называется кратчайшее расстояние от линии действия силы до оси вращения: (рис. 2, заметим, что , где - вектор момента силы относительно точки О, лежащей на оси вращения, а вектор проведен от О к точке приложения силы).

Рис. 2. Момент силы относительно оси

3. Из законов Ньютона следует, что угловое ускорение пропорционально моменту силы:. Эту пропорциональность можно выразить уравнением

, (1)

где - момент инерции твердого тела (диска) относительно оси вращения.

4. Момент инерции определяет инерционные свойства твердого тела при вращении и зависит от распределения массы в объеме этого тела. По определению момент инерции тела относительно оси равен

, (2)

где - элементарная («точечная») масса, на которые мысленно разбивается тело, - расстояние от этой массы до оси вращения (рис.3).

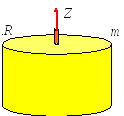
Рис.3. К определению момента инерции	Рис. 4. Момент инерции кольца	Рис. 5. Момент инерции цилиндра

Если твердое тело представляет собой тонкое кольцо радиуса R и массы m, то момент инерции относительно оси, перпендикулярной плоскости кольца и проходящей через его центр равен (рис. 4).

.

При вычислении момента инерции однородного цилиндра (или диска) относительно оси, совпадающей с его осью симметрии, следует учесть, что величины в выражении не равны радиусу диска R, а изменяются для разных элементарных масс от 0 до R. После вычисления этой суммы (интегрирования) получим для момента инерции цилиндра , где - масса цилиндра.

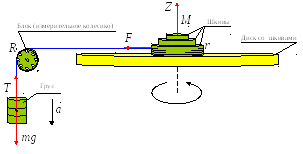
5. В данной лабораторной работе момент инерции твердого тела определяется экспериментально. Полученное значение I сравнивается с рассчитанным по формуле . Твердое тело представляет собой алюминиевый диск, на котором закреплены три шкива, предназначенные для наматывания нити. Диск соединен через блок легкой нитью с грузом массы m, который, опускаясь под действием силы тяжести, приводит диск во вращение. Схема установки изображена на рис. 6.

Диск вращается под действием момента силы натяжения нити , равного , где – радиус шкива.

Рис. 6. Схема экспериментальной установки

Если пренебречь массой нити, массой блока и трением в его оси, то , где F и T - силы натяжения нити, действующие соответственно на шкив и груз. Пренебрегая также трением в оси диска, запишем уравнение (1) в виде:

, (3)

где I – момент диска с закрепленными на нем шкивами.

Воспользуемся также вторым законом Ньютона для поступательного движения груза:

. (4)

Если нить нерастяжима, то ускорение поступательного движения груза a и угловое ускорение диска связаны соотношением:

. (5)

Исключая величины T и a из системы уравнений (3) - (5), получим:

. (6)

При из формулы (6) следует:

(7)

Из этой формулы следует, что угловое ускорение пропорционально массе груза. Формула (7) и проверяется в данной лабораторной работе экспериментально:

• при разных массах m измеряется угловое ускорение,

• строится график зависимости от ,

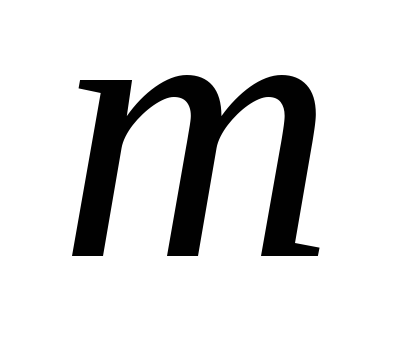• проверяется линейность этого графика,

• по угловому коэффициенту определяется момент инерции диска I,

• полученное значение I сравнивается с рассчитанным по формуле .

6. Чтобы определить угловое ускорение для каждого значения m измеряется зависимость угла поворота диска от времени. При вращении диска с постоянным угловым ускорением из уравнения следует , где - угловая скорость при . А из уравнения следует . Считая, что при диск не вращался и угол , получим

.

Согласно этому уравнению график зависимости от должен быть линейным с угловым коэффициентом . По угловому коэффициенту определяется угловое ускорение диска при каждом значении .