Лабораторная работа №10 «определение скорости распространения звуковых волн в воздухе и твердых телах»

Цель работы: Изучение закономерностей распространения колебательных процессов в упругих средах.

Вопросы для допуска к работе

1. Что представляет собой волновой процесс?

2. Чем отличается распространение волн в неограниченных и ограниченных средах.

3. Что такое стоячая волна, её длина?

4. Какими способами можно определить длину волны в среде?

5. В чём заключается смысл способа определения скорости звука в воздухе по Квинке?

6. Опишите способ определения скорости звука в воздухе методом сложения взаимно перпендикулярных колебаний.

Литература

1. Савельев И.В. Курс общей физики. - М., т.1, 1962, с. 209-235.

2. Архангельский М.М. Курс физики. Механика. – 1973, с.319 -327

3. Стрелков С.П. Механика. - М., 1965, с. 459-489.

4. Ландсберг Г.С. Элементарный учебник физики. - М., т.III, 1962, с. 79 - 115.

Сведения из теории

I. Распространение колебаний в упругой среде.

Рассмотрим процессы, происходящие в упругой среде под действием периодической силы. Пусть источником периодической силы является колеблющееся тело. Частицы среды, непосредствен­но прилегающие к телу, будут также участвовать в колебатель­ном движении. В результате упругого взаимодействия их с сосед­ними частицами последние также начнут колебаться. Таким обра­зом, колебания будут передаваться от одних точек к другим с конечной скоростью. Упругостью сжатия и растяжения обладают все тела: твердые, жидкие, газообразные, поэтому колебания могут распространяться в любых телах.

Процесс распространения колебаний в какой-либо среде на­зывается волной. В результате распространения волны ча­стицы будут совершать колебания около положения равновесия. При этом происходит передача энергии без переноса вещества.

Если колебания происходят вдоль того же направления, что и распространение энергии, то такие волны называются продольными. Если же направления колебания частиц перпен­дикулярны к направлению распространения энергии, то такие волны называются поперечными.

Продольные волны обусловлены деформацией сжатия и растя­жения, поперечные - деформацией сдвига. В твердых телах могут распространяться как продольные, так и поперечные волны. В жидкостях и газах деформации сдвига не упруги, т.е. сдвинутые друг относительно друга слои жидкости не возвращаются в исходное состояние.

Поэтому в жидкостях и газах могут распространяться только продольные волны. Поперечные и продольные волны описываются уравнениями одного и того же вида.

II. Уравнение плоской бегущей волны.

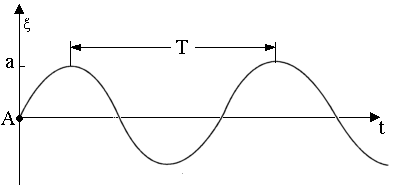
Рассмотрим процесс распространения колебаний вдоль оси х, источником которых является точка А (рис. 1), колеблющаяся по закону: .

Соседние точки придут в колебание с той же амплитудой a и частотой , что и точка А, но с некоторым опозданием. Время начала колебания точки В, находящейся на расстоянии х от источника, отстанет от времени начала колебаний точки А на время , где v – скорость распространения волны в данной среде.

Рис.1

Если величина смещения точки А от положения равновесия в момент t равна (1), то, вследствие запаздывания, сме-щения точки В в тот же самый момент времени t будет или

(2)

Уравнение (2) называется уравнением плоской бегущей волны. Таким образом, из уравнения (2) следует, что смещение произвольной точки зависит от двух переменных: расстояния х от точки до источника и времени наблюдения t.

Расстояние, на которое распространяется колебание за время, равное одному периоду, называется длиной волны . Понятно, что (3), где T – период колебаний.

Так как , то уравнение бегущей волны можно переписать в виде:

.

Из сопоставления последнего выражения с уравнением (1), видно, что колебания точки В с координатой х сдвинуто по фазе относительно колебаний в точке А на .

Определим фазу колебаний в точке С, отстоящей от точки В на расстоянии, равном длине волны . Фаза точки В равна: , тогда (4), т.е. фазы точек с координатами х и х+ совпадают. Поэтому длину волны можно определить как минимальное расстояние между двумя точками, колеблющимися в одинаковых фазах.

Так как за время Т колебательный процесс распространился на расстояние , то скорость распространения колебаний можно представить в виде:

(5),

где - частота колебаний.

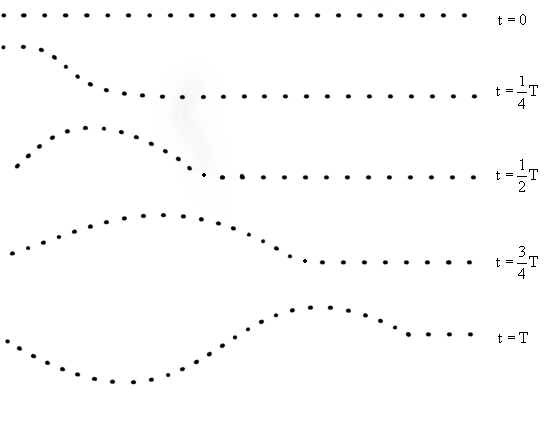
На рис.2 изображены положения точек образующейся волны для пяти последовательных моментов времени через четверть периода.

Рис. 2