13. Лінія як елемент резонансного ланцюга

Чвертьхвилева лінія з малими втратами, розімкнена на кінці, володіє якостями резонансного ланцюга, який складається з послідовно з'єднаних r, L і С. При частоті, при якій на лінії вкладається чверть хвилі (таку частоту умовимся називати резонансною), вхідний опір лінії буде активним і при цьому мінімальним.

При малому відхиленні частоти від резонансної модуль вхідного опору лінії різко зростає; вхідний опір набуває ємнісного характеру при зниженні частоти і індуктивний характер при підвищенні.

Вхідний опір лінії з малими втратами, розімкнений на кінці, можна отримати з (1.16), якщо розкласти shx' та chx' по формулам тригонометрії і зважаючи на малость , ch x' 1, a sh x' x',

Вираз прийме вид:

Поблизу резонансної частоти  x'/2 і sinx' 1, a cosx'1l. Тому

Якщо через ₀ позначити коефіцієнт фази при резонансній частоті, т. ч. прийняти ₀x'=/2 і врахувати співвідношення то cos₀ x' можна перетворити слідуючим чином:

Тут - розладнання частоти по відношенню до резонансної. Отже

При частоті, близькій до резонансної, коли величина  значно менше одиниці, комплексний опір резонансного ланцюга приблизно дорівнює:

Розглядаючи чвертьхвилеву лінію як резонансний ланцюг, можна в силу однакової структури попередніх виразів рахувати, що добротність лінії рівна:

Відповідно смуга пропускання, що подає величину, зворотню добротності, дорівнює:

Тут під смугою пропускання мають на увазі віднесену до резонансної частоти ширину резонансної кривої між точками, відповідними половині максимальної потужності .

При малих значеннях коефіцієнту  добротність одержується високою, досягаючою приблизно 1000 - 4000, що перевищує добротність контурів r, L, С. В зв'язку з цим зростає і гострота настройки.

14. Перехідні процеси в лініях з розподіленими параметрами

Перехідні процеси в ланцюгах з розподіленими параметрами виникають при комутаціях, при передачі неперіодичних сигналів або під впливом зовнішнього електромагнітного поля (наприклад, при грозових розрядах). Для дослідження перехідних процесів в однорідних ланцюгах з розподіленими параметрами користуються диференційними рівняннями (1.1) в поодиноких похідних.

В загальному вигляді рішення цих диференційних рівнянь достатньо складне. Рішення спрощується, якщо знехтувати втратами, т. ч. рахувати, що r₀ та g₀ дорівнюють нулю. В цьому випадку рівняння приймають вигляд

Якщо диференціювати перше рівняння по х:

і підставити друге рівняння, одержимо:

Це диференційне рівняння відомо в математичній фізиці під назвою рівняння коливань струни. Його рішення дане Даламбером і має вигляд:

(1.51)

Де називається швидкістю хвилі і чисельно рівна фазовій швидкості.

Перший доданок подає собою одиночну пряму хвилю напруги, що без зміни переміщається в сторону зростаючих х, т. ч. від початку до кінця ланцюга. Для всіх значень х, при яких х - vt = const, цей доданок має одне і те ж значення, т. ч. хвиля рухається зі швидкістю v=dx/dt.

Другий доданок подає собою одиночну обернену хвилю напруги, що без зміни переміщується в протилежному напрямі.

Для струму справедливий вираз

(1.52)

Вирази (1.51) і (1.52) записуються скорочено

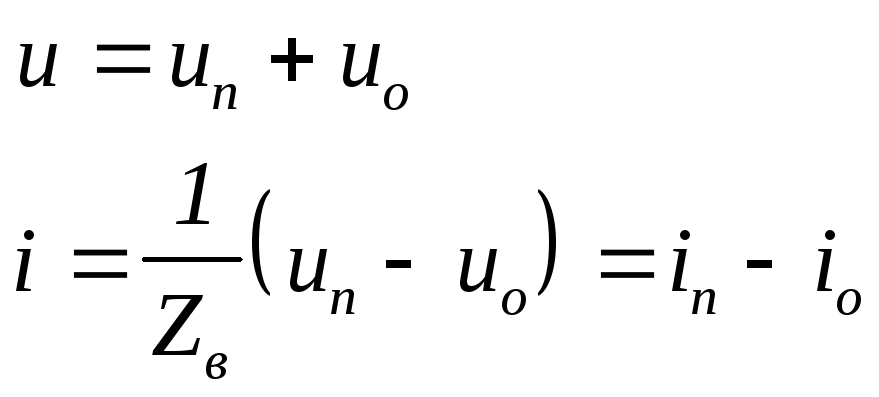(1.53)

Тут i_п і i_о- пряма і обернена хвилі струму; - хвильовий опір.

Отже, напруга і струм прямої і оберненої хвиль зв'язані законом Ома:

Отже, за відсутності втрат в однорідному ланцюзі з розподіленими параметрами напруга і струм можуть бути представлені як сума і як різниця двох хвиль, які рухаються з однаковою швидкістю в протилежних напрямах, без зміни їхньої форми. При цьому в будь-якій точці однорідного ланцюга відношення напруги і струму для прямої і оберненої хвиль рівно хвильовому опору Z_в.

Якщо на шляху розповсюдження хвилі зустрічається неоднорідність, наприклад повітряна лінія переходить у кабельну або хвиля досягає кінця лінії (розімкнутого, замкнутого на опір, коротко замкненого), відбувається відбивання хвилі. В залежності від характеру неоднорідності відбивання може бути частковим або повним. В першому випадку наряду з відбитою хвилею виникає переломлена хвиля, що розповсюджується за місце порушення однорідності; в другому випадку переломлена хвиля буде відсутня. Позначимо:

u₁, i₁ - напруга і струм в місці відбивання;

u_1п, i_1п - напруга і струм падаючої (прямої) хвилі;

u_1о, i_1о - напруга і струм відбитої (оберненої) хвилі;

u₂, i₂ - напруга і струм переломленої (прямої) хвилі;

Z₁, Z₂ - хвильові опори для прямої і оберненої хвиль (Z₁) і переломленої хвилі (Z₂).

В місці неоднорідності виконується умова рівності напруг і струмів:

Отже,

Підстановка значень

В результаті спільного рішення цих рівнянь знаходяться відбита (u_1о) і переломлена (u₂) хвилі:

Де - коефіцієнт відбивання.

Відповідно струм відбитої хвилі

А струм переломленої хвилі

Останній вираз показує, що струм в кінці лінії після відбивання можна знайти як струм в еквівалентному ланцюзі, в який вмикається напруга, що дорівнює подвійній напрузі падаючої хвилі, і який складається з хвильового опору першої лінії Z₁ і послідовно з'єднаного з ним опору навантаження (в який входить друга лінія своїм хвильовим опором Z₂).