Текст программы на языке qbasic имеет вид

DEF FNlx (k, c1, c2, x1)

L = 0

FOR i = 0 TO k

L1 = 1

FOR j = 0 TO k

IF j <> i THEN L1 = (x1 - x(j)) * L1 / (x(i) - x(j))

NEXT j

L = L + L1 * y(i)

FNlx = L

NEXT i

END DEF

x1 = .57

n = 5

E = .001

DATA 0.50,0.55,0.60,0.65,0.70,0.75

DATA 0.8871,1.0265,1.1752,1.3366,1.5095,1.696

FOR i = 0 TO n

READ x(i)

NEXT i

FOR j = 0 TO n

READ y(j)

NEXT j

k = 2

L = FNlx(k, x(5), y(5), x1)

L(k) = L

n2: a = L

k = k + 1

L = FNlx(k, x(5), y(5), x1)

L(k) = L

E1 = ABS(L - a)

IF E1 <= E THEN GOTO n1

IF k >= n THEN GOTO n1

GOTO n2

n1: WRITE "mnogochlen Lagranga pri x=", x1, " raven ", L, "E1=", E1

END

Ответ программы

mnogochlen Lagranga pri x= 0.57 raven L = 1.084674, E1 =1.903772E-04

mnogochlen Lagranga pri x= 0.62 raven L = 1.238045, E1 =7.616282E-04

Блок-схема программы интерполяции по формуле Лагранжа имеет вид:

начало x₁ – значение аргумента, при котором вычисляется м многочлен Лагранжа

n + 1 – число узлов интерполяции

Ввод

x_1, n, E Е – требуемая точность интерполяции

j = 0, n

Ввод x(0:n) – массив значений аргумента в узлах

x(i), y(j) интерполяции

y(0: n) – массив значений функции в узлах

интерполяции

k = 1

L = lx() Вызов процедуры-функции lx (k, x(),y(), x1) L(k) = L для вычисления многочлена Лагранжа k -й степени

в точке x = x₁

A = L

k = k + 1

Вызов процедуры-функции lx (k, x(),y(), x1)

L = lx() для вычисления многочлена Лагранжа k + 1-й степени

L(k) = L и нахождение Е1 для достижения необходимой

Е1 =|L – A| точности вычислений.

да нет

Е1<=E

или

k>= n

да

Вывод Вывод значений многочлена Лагранжа k - й в точке

L(1:k) x = x1.

Рис.1

Блок-схема программы вычисления процедуры-функции lx() вычисления многочлена Лагранжа k – й степени в точке х1.

lx ()

L = 0 Описание процедуры-функции

lx(входные параметры:

k –степень многочлена Лагранжа,

i = 0, k x(0: k) – массив значений

аргумента в узлах интерполяции,

y(0: k) – массив значений

в узлах интерполяции,

L1 = 1 x1 – значение аргумента, при

котором вычисляется

многочлен Лагранжа

j = 0, k

нет

i <> j

да

Вычисление слагаемых.

L = L + L1*y(i) L – значение полинома

в точке x1.

lx = L Значение многочлена Лагранжа

Рис . 2.

Интерполяция возможна также с помощью пакета программ MathCAD.

При линейной интерполяции аппроксимирующая функция соединяет опытные точки отрезками прямых линий. Для линейной интерполяции используется встроенная функция linterp. Обращение к функции

linterp (X, Y, t)<

где X – вектор опытных значений аргумента; Y – вектор опытных значений функции; t – значение аргумента, при котором вычисляется интерполирующее значение функции.

В предыдущем примере имеем

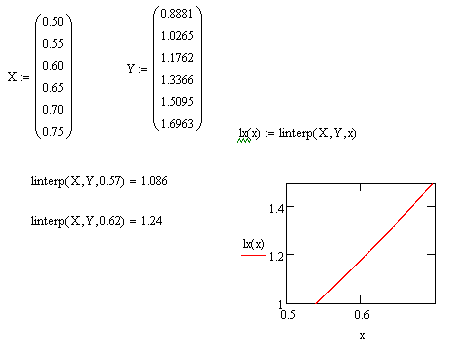
Обращаемся к пиктограмме «встроенная функция f(x)» на второй строке текстового окна стандартной линейки. В появившемся диалоговом окне в разделе «Категория функции» выбираем «Интерполяция», linterp, подставляем значения X, Y, 0.57 или 0.62 и получаем значения многочлена Лагранжа в этих точках. Используя функцию linterp(X, Y,x) можно построить график интерполирующей функции.