Одномерная оптимизация.

Оптимизация задачи – это процесс выбора наилучшего решения из множества возможных.

Одномерная оптимизация – это процесс нахождения экстремума функции одной переменной.

Пусть f(x) – функция, определенная на промежутке [a, b].

Функцию f(x) называют унимодальной, если на отрезке [a, b] существует единственная точка х^*, в которой f(x) принимает экстремальное значение.

Для определенности будем считать, что речь идет о минимуме функции (в случае максимума, взяв функцию –f(x), сведем задачу к нахождению минимума). Функция f(x) называется целевой функцией, аргументы х называются параметрами.

Отметим, что функция f(x) не обязательно должна быть гладкой или даже непрерывной. Из определения унимодальности следует, что если х₁ < x₂ ≤ x^*, то f(x₁) > f(x₂). Аналогично, если x^* ≤ x₁ < x₂ , то f(x₁) < f(x₂).

Интервал x _i-1 ≤ x^* ≤ x _i называется интервалом неопределенности. Алгоритм выбора абсцисс {x _i} называется стратегией поиска.

Оптимальной стратегией поиска называется та, которая при заданном количестве вычислений, дает наименьший интервал неопределенности.

Один из путей более эффективного поиска точки x^* состоит из построения вложенных отрезков [a₁, b₁], [a₂, b₂], ... [a_i , b _i], содержащих точку минимума. Действительно, пусть

a _i < x ₁ < x ₂ < b _i. Сравним f(x) в пробных точках.

Если f(x₁) ≤ f(x₂), то можно сократить отрезок поиска точки x^*, перейдя к отрезку [a_i, x ₂] . Если f(x₁) ≥ f(x₂) то можно перейти к отрезку [x ₁, b _i].

f(x₁) ≤ f(x₂) f(x₁) ≥ f(x₂)

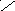
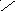
a_i x^* x^*

x₁ x ₂ b_i a_i x ₁ x₂ b_i

Решение достигается при получении заданной точности Е, т. е. при условии, что длина отрезка, на котором расположено значение х^* , меньше Е, и x^* равно половине длины этого интервала..

Способ получения точек х₁ и х₂ определяет метод оптимизации. Мы рассмотрим два метода: метод дихотомии и метод золотого сечения.

Метод дихотомии.

В этом методе пробные точки х₁ и х₂ располагаются близко к середине рассматриваемого отрезка [a, b].

(1)

Здесь h – малое число.

В конце вычислений в качестве приближенного значения х^* берут середину последнего из найденных отрезков, убедивших предварительно, что достигнуто неравенство

Алгоритм метода дихотомии следующий.

Шаг 1. Определить х₁ и х₂ по формулам (1) и вычислить f(x₁) и f(x₂). Перейти к шагу 2.

Шаг 2. Сравнить f(x₁) и f(x₂). Если f(x₁) ≤ f(x₂), то перейти к отрезку [a, x₂], положив

b = x₂. Если f(x₁) ≥ f(x₂), то перейти к отрезку [x₁, b], положив a = x₁. Перейти к шагу 3.

h h

f(x₁) ≤ f(x₂)

a x₁ O x₂ b

f(x₁) ≥ f(x₂), a x₁ h h x₂ b

O

Шаг 3.Найти достигнутую точность (здесь n – номер итерации). Если Е_n больше заданной точности Е, то перейти к следующей итерации, вернувшись к шагу 1.

Если E_n < E, то завершить поиск х^*, перейдя к шагу 4.

Шаг 4. Положить xmin = (a + b)/2.

Блок-схема программы нахождения минимума методом дихотомии.

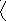
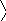
Начало

Описание

процедуры-функции

Ввод dih(x)

a, b, h, E

[a, b] – отрезок неопределенности

x1 = (a + b − h)/2 h – параметр метода

x2 = (a + b + h)/2 Е – точность оптимизации.

dih(x1) < dih(x2)

да нет Определение границ нового

b = x2 a = x1 отрезка неопределенности.

|b – a| < E

да

xmin = (a + b)/2 Точка минимума.

Вывод xmin

End

При использовании метода дихотомии надо учитывать следующее.

1. Величина h не может быть слишком малой, т. к.при при чрезмерно малом h сравнение функций в точках х₁ и х₂ затруднительно.

2. Величина h не может быть слишком большой, т.к. погрешность E > 2h/

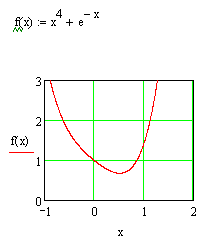
П р и м е р. Методом дихотомии с точностью Е = 0. 1 найти минимум функции

f(x) = x⁴ + e^{– x}

Используя пакет MathCAD,. строим график этой функции. В интервале [0, 1] функция имеет один минимум (унимодальная).

DEF FNdih (x) = x ^ 4 + EXP(-x)

a = 0

b = 1

h = .02

E = .1

m1: x1 = (a + b - h) / 2

x2 = (a + b + h) / 2

IF FNdih(x1) < FNdih(x2) THEN

b = x2

GOTO m2

END IF

a = x1

m2: IF ABS(b - a) > E THEN GOTO m1

x0 = (a + b) / 2

WRITE "xmin=", x0

END

Ответ программы xmin = 0.5306.

Для нахождения минимума используется встроенная функция Minimize

Метод золотого сечения.

Метод дихотомии, хотя и является простым в использовании методом, имеет существенный недостаток. Этот недостаток состоит в том, что на каждом шаге итерации функцию приходится вычислять дважды. Этот недостаток преодолен в методе золотого сечения.

Золотым сечением называют деление отрезка на две части так, что отношение длины всего отрезка к длине большей части равно отношению длины большей части к длине меньшей части.

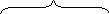х₂

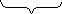l – x₂

A x₁ С₁ C B x

AB = l, AC = x₂, CB = l - x ₂

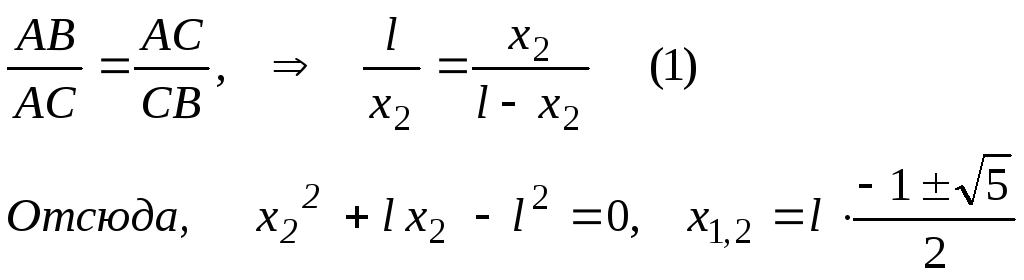
Взяв только положительное значение, получим

Из соотношения (1) следует, что если от точки А отложить отрезок АС₁ , равный l – x₂, то получим точку x₁, которая дает золотое сечение отрезка АС. Таким образом. находим две пробные точки рассматриваемого отрезка. Далее, в зависимости от соотношения между значениями функции в точках С и С_1, отсекаем часть отрезка АВ (АС₁ или СВ). На оставшемся отрезке сохранится одна пробная точка. Вторую точке найдем по правилу «золотого сечения.

Опишем алгоритм поиска.

Шаг 1. Начальный отрезок [a,b] делим точками х₁ и х₂ по «правилу золотого сечения».

Вычисляем значения функции f(x₁) и f(x₂) и E_n = ^{(b – a)} / ₂ . Переходим к шагу (2).

Шаг 2. Проверка окончания поиска: если Е_n > E , то переходим к шагу 3, иначе к шагу 4 (Е – допустимая погрешность вычисления точки минимума).

Шаг 3, Переход к новому отрезку и новым пробным точкам.

Если f(x₁) ≤ f(x₂), то полагаем b = x₂, x₂ = x₁, f(x₂) = f(x₁), x ₁ = a + (b – a) α., вычисляем f(x₁).

Если f(x₁) ≥ f(x₂), то полагаем a = x₁, x₁ = x₂, f(x₁) = f(x₂), x₂ = a + (b – a) β, вычисляем f(x₂), E_n = (b – a)/2. Перейти к шагу 2.

Шаг 4. Окончание поиска: положить х^* =.

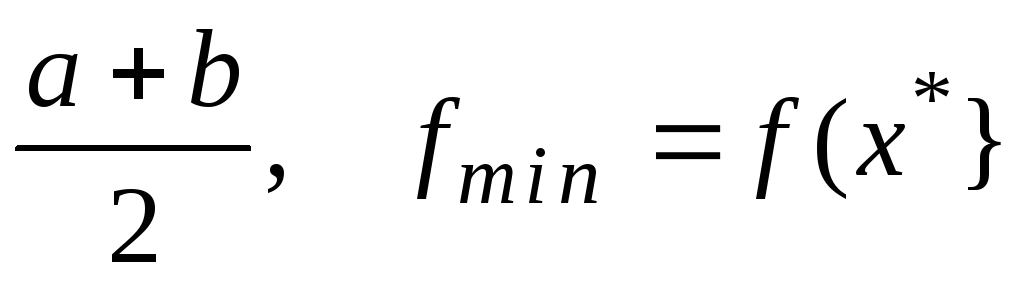Блок-схема программы нахождения минимума методом «золотого сечения».

Начало

Описание

процедуры-функции

Ввод gs(x)

a, b, E

[a,b] – отрезок неопределенности

α = 0.38197 Е – точность оптимизации

β = 0.61803

x1 = a + (b – a)

x2 = a + β(b – a)

f1 = gs(x1)

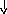f2 = gs(x2)

нет да

f1< f2

a = x1, x1 = x2 b = x2, x2 = x1,

x2 = a + β (b – a) x1 = a + α (b-a)

f1 = f2 f2 = f1

f2 = gs(x2) f1 = gs(x1)

нет |b – a| < E

да

xmin =

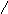
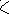
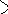
Вывод xmin end

П р и м е р Методом «золотого сечения» найти точку минимума функции f(x) = x² + e^x.

Используя пакет MathCAD, строим график этой функции.

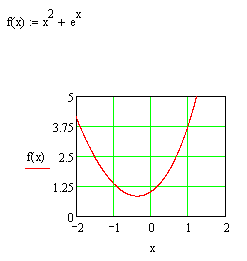
Из графика видно, что функция имеет минимум в интервале [-1, 0]

Программа нахождения минимума методом «золотого сечения» имеет вид.

DEF FNgs (x) = x ^ 2 + EXP(x)

a = -1

b = 0

E = .001

alfa = .38197

beta = .61803

x1 = a + alfa * (b - a)

x2 = a + beta * (b - a)

f1 = FNgs(x1)

f2 = FNgs(x2)

m2: IF f1 < f2 THEN

b = x2

x2 = x1

x1 = a + alfa * (b - a)

f2 = f1

f1 = FNgs(x1)

GOTO m1

END IF

a = x1

x1 = x2

x2 = a + beta * (b - a)

f1 = f2

f2 = FNgs(x2)

m1: IF ABS(b - a) > E GOTO m2

x0 = (a + b) / 2

WRITE "xmin=", x0

END

Ответ программы: xmin = -0.3517317.

Округляя с двумя дополнительными знаками, имеем xmin = -0.35173.

Находим минимум, используя пакет MathCAD.

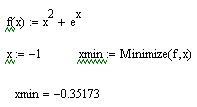
Для нахождения минимума используется встроенная функция Minimize

Многомерная оптимизация.

Общая задача нелинейного программирования без ограничений состоит в нахождении минимума функции, зависящей от n переменных f(x) = f(x₁, x₂, ...,x_n). Функция f(x) называется целевой функцией, где (x – вектор {x₁, x₂, ..., x_n).

Как правило, численные методы отыскания экстремума состоят в построении последовательности векторов {x ^(k)}, удовлетворяющих условию f(x ⁽⁰⁾) > f(x ⁽¹⁾) > ... > f(x ⁽ⁿ⁾). Методы построения таких последовательностей называются методами спуска. В этих методах элементы последовательности {x ^(k)} вычисляются по формулам

x ^{(k + 1)} = x ^(k) – α g ^(k), (k = 0, 1, 2, ..., ) (1)

Здесь g ^(k) – направление спуска, α – длина шага в этом направлении. Как известно, градиент функции в точке направлен в сторону наискорейшего возрастания функции в этой точке. Следовательно, спускаться надо в направлении, противоположном градиенту. Вектор. противоположный градиенту, называется антиградиентом. Выбирая антиградиент в качестве направления спуска, приходим к итерационному процессу вида (1), где

g ^(k) =

Мы будем рассматривать метод градиентного спуска с дроблением шага.

Алгоритм метода градиентного спуска с дроблением шага следующий

y

x

Шаг 1. Задать параметр точности Е, начальный шаг α > 0, выбирать начальное значение (начальную точку) х. Общих правил для нахождения х нет. Если есть какие-либо сведения об области существования минимума рассматриваемой функции, то выбираем х из этой области. Вычислить f (х⁾) и перейти к шагу 2.

Шаг 2. Вычислить и проверить условие достижения точности | < E. Если это условие выполняется, то вычисления закончить, полагая xmin = x, вычислить f(x). иначе перейти к шагу 3.

Шаг 3. Найти и f(x1). Если f(x1) < f(x), то положить x = x1, f(x) = f(x1) и перейти к шагу 2, иначе к шагу 4.

Шаг 4. Положить α = α/ 2 и перейти к шагу 3.

Блок-схема программы нахождения минимума функции методом градиентного спуска.

Ввод n – размерность пространства,

n, α, E, x(). в котором задана целевая функция f(x), α – начальный шаг, Е – параметр точности вычислений, x () массив, в в котором размещены координаты начальной точки х ⁽⁰⁾ спуска .

Описание процедуры k = 0

процедуры gr(x, g,y) количество итераций

вычисления градиента g

и значения целевой s = 0

функции у.

i = 1, n

обращение к процедуре

gr(x(), g(), y)

s = s + (g(i))² Вычисление градиента

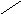
s < E Проверка достижения точности

нет

k = k + 1

Вывод x1min, x2min

k, fmin

j = 1, n

End

x1(j) = x(j) – α g(j)

gr (x1(),g1(), y1)

y1 < y

да

нет

y =y1

α = ½ α Дробление шага

xI(i) = x1(i) i = 1, n