Текст программы на языке qbasic интегрирования по формуле прямоугольников.

Формула трапеций.

Более точное значение интеграла получится, если данную кривую заменим не ступенчатой линией, как это было в формуле прямоугольников, а вписанной ломаной такой, что криволинейная трапеция заменяется суммой площадей прямолинейных трапеций.

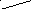
y₂ y _i y _i+1 y _n

y₁

y₀

x₀= a x₁ x₂ .... x _i x _{i + 1} ... b = x _n

Разобьем интервал [a, b] на n равных частей. Длину частичного интервала обозначим

h = ^{(b – a)} / _n

(*)

Число n выбирается произвольно. Чем больше будет это число и, следовательно, чем меньше будет шаг h, тем с большей точностью формула (*) будет давать значение интеграла.

Аналогично формуле прямоугольников, для оценки погрешности применим метод Рунге. По формуле (*) проводим вычисления дважды: при вычислениях на n и на 2n частей; приближенные значения интеграла обозначим соответственно J _n и J_2n . С помощью метода Рунге было доказано, что погрешность при этом удовлетворяет неравенству

Формула парабол (формула Симпсона, 1710-61, Англия).

Большей точностью обладает квадратурная формула или формула парабол (или формула Симпсона). Разобьем отрезок [a, b] на четное число равных частей n = 2m.

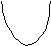
Площадь криволинейной трапеции, соответствующей первым двум отрезкам [x₀, x₁] и [x ₁, x ₂] и ограниченной кривой y = f(x), заменим площадью криволинейной трапеции, ограниченной параболой с осью симметрии, параллельной оси Оу. Эта парабола проходит через точки М(x ₀, y₀), M₁(x ₁, y₁) и M₂(x ₂, y₂).

y

M₃ M₄

M

M₅ y =f(x)

M₁ M₂

M₆

a = x₀ x₁ x₂ x₃ x₄ x₅ x₆ = b x

Чтобы написать уравнение этой параболы, используем многочлен Ньютона второго порядка

h = ^{(b – a)} / _2n

Δy₀ = y₁ – y₀, Δ²y₀ = Δy₁ – Δy₀ = y₂ – y₁ – y₁ + y₀ = y₂ – 2y₁ + y₀.

Площадь под параболой имеет вид

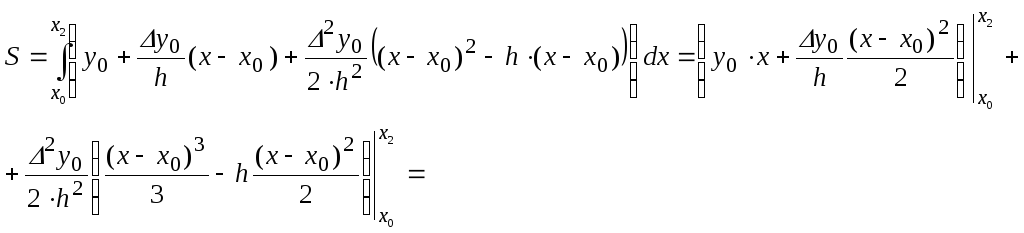
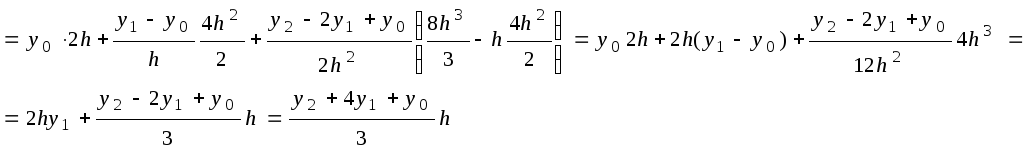Вернувшись к основной задаче, аналогично, получим

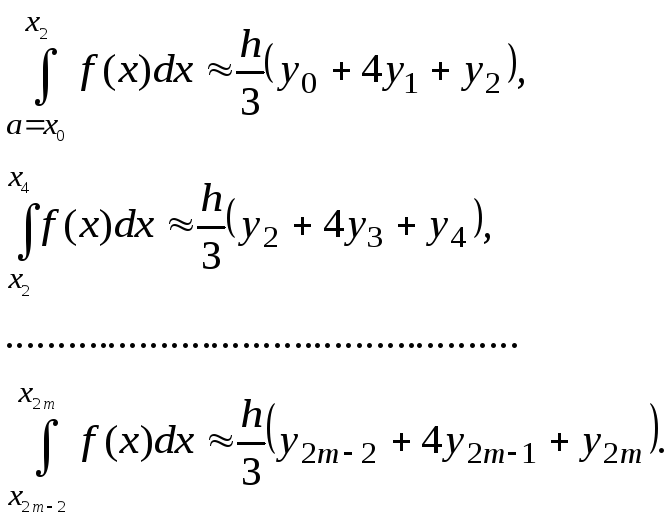
Складывая левые и правые части, получим

. (**)

Это и есть формула Симпсона. Здесь число точек деления 2m произвольно, но чем больше m, тем точнее формула Симпсона дает значение интеграла.

Аналогично формулам прямоугольников и трапеции, для оценки погрешности применим метод Рунге. По формуле (**) проводим вычисления дважды: при вычислениях на n и на 2n частей; приближенные значения интеграла обозначим соответственно J _n и J_2n . С помощью метода Рунге было доказано, что погрешность при этом удовлетворяет неравенству

Блок-схема программы вычисления интеграла по формуле Симпсона

Описание оператора

функции

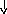
Ввод a, b – пределы интегрирования

a, b, E Е – заданная точность вычисления

интеграла

n = 2

h = (b – a)/ n

s = (f(a) + 4*f((a + b)/2 +f(b))*(h/3) s –значение интеграла

n = 2*n, h = (b – a)/ n

s1 = s, c = 4, x = 0

s = f(a) + f(b)

i = 1, n - 1

x = x + h

s = s + c*f(x)

c = 6 – c

.

да |s – s1|/15 >= E

Вывод

s, n.

end

П р и м е р . Вычислить используя формулу Симпсона . Погрешность Е=0. 0001. Ответ формулы =0.5673363, n = 256.