Прямоугольный треугольник: тригонометрические соотношения
Задачи
1. Через точки А
и В,
принадлежащие окружности, проведены
касательные, пересекающиеся в точке М,
,
.
Найти радиус окружности.
2. В выпуклом
четырёхугольнике MNLQ
углы при вершинах N
и L
– прямые, а тангенс угла при вершине M
равен
.
Найти диагональ NQ,
если известно, что сторона LQ
вдвое меньше стороны MN
и на 2 больше стороны LN.
3. Треугольник KMN
остроугольный,
,
.
Найти отношение высот NP
и MQ.
4. На катете АС
прямоугольного треугольника АВС
как на диаметре построена окружность,
которая пересекает гипотенузу АВ
в точке K.
Найти площадь треугольника CKB,
если катет
,
а
.
5. Радиус окружности,
вписанной в ромб, равен r,
а острый угол ромба равен
.
Найти сторону ромба.
6. Общая хорда двух пересекающихся окружностей видна из их центров под углами 90° и 60°. Найти радиусы окружностей, если расстояние между их центрами равно а. (Центры могут лежать по разные стороны от хорды, а могут и по одну сторону.)
7. Две вершины квадрата расположены на основании равнобедренного треугольника, а две другие – на его боковых сторонах. Найти сторону квадрата, если основание треугольника равно а, а угол при основании равен 30°.
8. Высота треугольника
АВС,
опущенная на сторону ВС,
равна h,
,
.
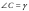Найти остальные высоты этого треугольника.
10. Дан прямоугольный треугольник, один из углов которого равен 30°. Из середины его гипотенузы восставлен серединный перпендикуляр к ней. Доказать, что длина этого перпендикуляра, лежащего внутри треугольника, равна трети длины большего катета.
9. Радиус окружности,
описанной около равнобедренного
треугольника, равен R.
Угол при основании равен
.
Найти стороны треугольника.
10. Дан отрезок
длиной 1. Построить отрезки длиной
,
,
,
,
,
.
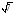11. Даны отрезки а
и b
(
).
построить отрезки длиной
,
,
,
.
12. Найти
(геометрически!)
,
,
.
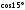13. Биссектриса одного из углов треугольника делит его на два равнобедренных треугольника. Найти углы треугольника.
14. Найти
,
,
.
15. Найти сторону правильного десятиугольника, вписанного в окружность радиуса R.
16. Высота треугольника, опущенная на основание, в два раза меньше его основания, а один из углов при основании 75°. Доказать, что треугольник равнобедренный.
17. Найти угол В
треугольника АВС,
если высота СН
равна половине стороны АВ
и
.
18. В треугольнике
АВС
.
Известно, что высота и биссектриса,
проведённые из вершины А,
образуют угол, равный 22°30ʹ. Найти
.
Задачи на «5»
19. В треугольнике
АВС,
таком что
,
,
проведены биссектриса
,
биссектриса
и высота
Найти площадь треугольника,
образованного пересечением прямых:
а) АС,
и
;
б)
,
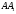и
20. Окружности радиусов 5 и 12, расстояние между центрами которых равно 13, пересекаются в точках А и В. Через точку В проведена прямая, пересекающая бóльшую окружность в точке K, а меньшую – в точке M, причём точка B лежит между точками K и M. Найти косинусы углов треугольника KAM.
ГЕОМЕТРИЯ – 5 2011