Краткие теоретические сведения

Известно, что практически любой периодический сигнал с периодом T=2 / ₁ можно представить тригонометрическим рядом Фурье

, (П1.1)

где A_n, _n – амплитуда и фаза n-й гармоники:

, , (П1.2)

здесь а_n , b_n – коэффициенты ряда Фурье:

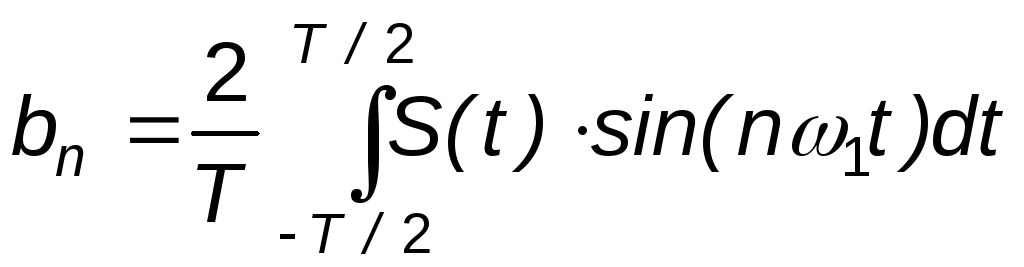, . (П1.3)

Постоянная составляющая сигнала, вычисленная в виде его среднего значения

,

является частным случаем алгоритма (П1.3) для n = 0 .

Так периодические униполярные импульсы прямоугольной формы (рис. П1.1) с амплитудой Е и длительностью импульса t_и запишутся в виде

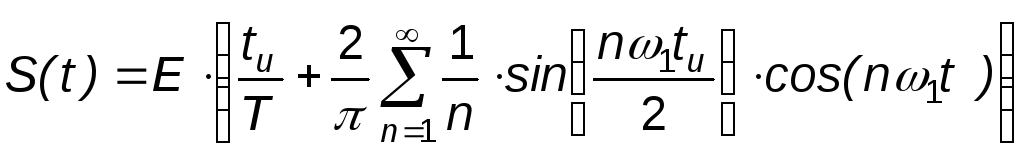. (П1.4)

введя скважность Q=T/ t_и и представив огибающую амплитуд А_n в форме sin(x)/ x, получим

, . (П1.5)

Рис. П1.1 Рис. П1.2

Для меандра (рис. П1.2, Q = 2, а₀ /2 = 0) как биполярного сигнала с амплитудой им-пульсов Е (то есть здесь скачок напряжения в импульсе составит 2Е ) получим частное представление (П1.5) в виде

, A_n = = 2E sinc(n / 2). (П1.6)

С учетом периодичности значений синуса: 1, 0, -1, 0, 1, 0, -1, ..., в (П1.6), соответствующих n = 1, 2, 3, 4, 5, ..., получаем знакочередующийся ряд из нечетных гармоник

. (П1.7)

при периодическом повторении одиночного импульса со спектром S(j) дискрет-

ный эквидистантный спектр периодизированного сигнала с периодом Т будет иметь следующие значения амплитуды и частоты n-й гармоники:

. (П1.8)

Известно, что относительная среднеквадратическая ошибка аппроксимации (назовем её погрешностью анализа _а ) сигнала S(t) конечным рядом Фурье оценивается по формуле

_а =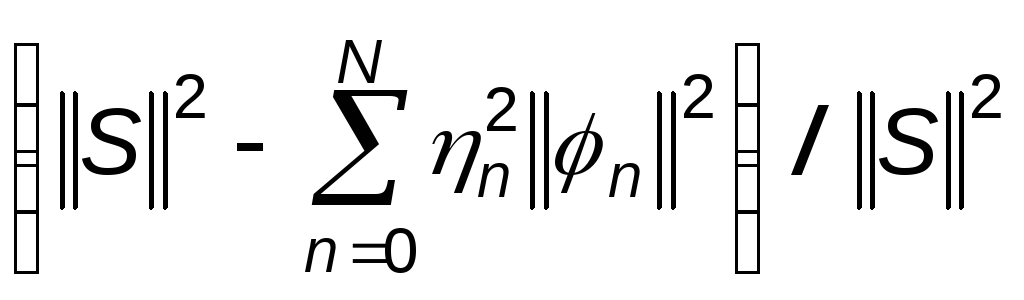, (П1.9)

где ||S||² – квадрат нормы периодического сигнала S(t) с периодом Т:

, (П1.10)

|| _n||² – квадрат нормы базисной функции  _n (t), ортогональной на периоде сигнала Т:

(П1.11)

_n - n-й коэффициент разложения сигнала S(t) в обобщенный ряд Фурье

. (П1.12)

При получаем .

погрешность анализа (П1.9) для сигнала на рис. П1.1 запишется в виде

_а = 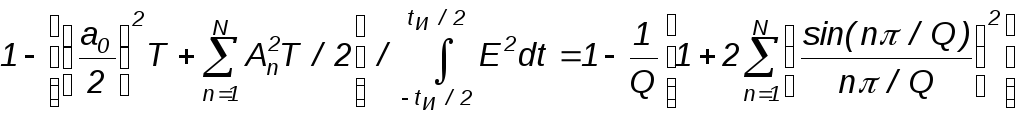. (П1.13)

В частности, при Q = 2

_a = . (П1.14)

К подобному же (но численно отличающемуся) результату придем и при определении погрешности (П1.9) непосредственно для меандра на рис. П1.2, где а₀ /2 = 0:

_а = 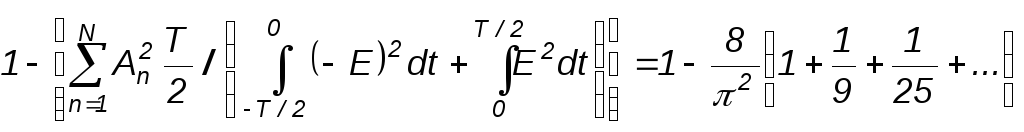. (П1.15)

Результат (П1.15) отличается от (П1.14): погрешность в два раза увеличилась, причем из-за отсутствия в меандре постоянной составляющей a₀ /2.

Аналогично получают формулы вычисления погрешностей и для других сигналов.

При использовании комплексно – экспоненциального базиса {exp(jn₁t)} обобщенный ряд Фурье принимает вид

, (П1.16)

В этом случае в общее выражение для погрешности (П1.9) следует подставлять || _n||² =Т, _n = = A_n /2, и погрешность (П1.13) для униполярного импульса (рис. П1.1) запишется несколько иначе:

_a =.

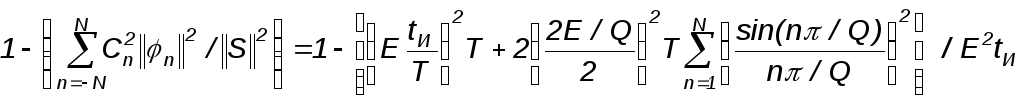Однако окончательный результат

_a = (П1.17)

полностью совпадает с погрешностью (П1.13). Это и следовало ожидать, так как для аппроксимации сигнала S(t) используется один и тот же гармонический ряд Фурье, имеющий различные формы представления.

Кроме рассмотренного спектрального способа определения погрешности аппроксимации (_а) сигнала S(t) существует ещё временной способ вычисления этой погрешности:

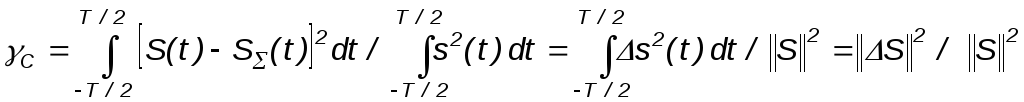, (П1.18)

где разность между исходным S(t) и восстановленным S_(t) сигналом.

Назовем _С погрешностью синтеза (в отличие от _а погрешности анализа). Но очевидно _С = _а, так как S_(t) выражается через тот же ограниченный спектр в (П1.9) и является конечным рядом Фурье

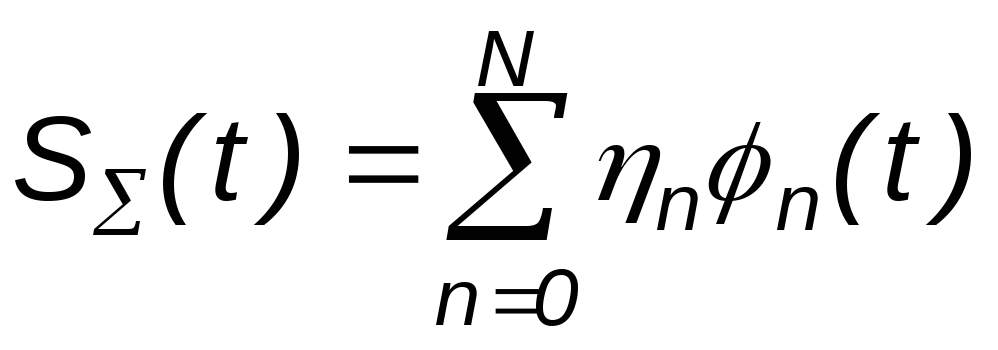. (П1.19)

Смысл введения _С состоит в том, что иногда удобнее вычислять погрешность аппроксимации непосредственно по осциллограммам или графикам (возможно и по аналитическим выражениям) сигналов S(t) и S_(t). при наличии осциллограмм прибегают к графическому интегрированию функций, то есть к вычислению площадей квадратов этих функций или сразу . по физическому смыслу площади и соответствуют энергиям ошибки и сигнала. по существу, равенство _С = _а в виде

(П1.20)

(чаще без в знаменателях) отражает известное равенство парсеваля на языке ошибок аппроксимации, которое в общем случае указывает на возможность вычисле-ния энергии сигнала как по собственно сигналу (временная функция), так и по его спектру.

На практике энергию спектрального "хвоста" в (П1.20) вычисляют не непос-редственно, а по (П1.9):

. (П1.21)

В заключение заметим, что формула (П1.21) и другие выражения связанные с определением погрешностей _С и _а, справедливы благодаря свойствам ортогональности базисных функций _n(t).

Приложение П1.2