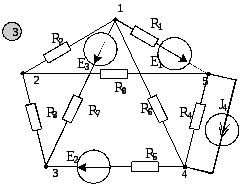
Пример выполнения расчетно-графичекой работы

Данные и схема варианта приведены ниже

R1	R2	R3	R4	R5	R6	R7	R8	E1	E2	E3	J
ом	ом	ом	ом	ом	ом	ом	ом	В	В	В	А
10	12	20	8	5	15	22	11	50	100	150	2

1. Рассчитать все токи, методом узловых потенциалов, используя матрично-топологический подход.

2. Рассчитать все токи, методом контурных токов, используя матрично-топологический подход.

3. Рассчитать баланс мощностей

4. Подтвердить расчеты пунктов 1, 2 ,проделав работу на ElectronicsWorkbench

5. Убрать ветвь с сопротивление R_8. Рассчитать ток в ветви с сопротивлением R₄ методом эквивалентного генератора. Построить выходную характеристику генератора и график зависимости мощности от тока P(I) и сопротивления нагрузки P(R_н)

• Выполняем первый пункт задания

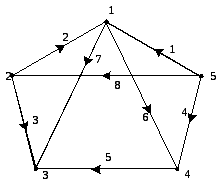
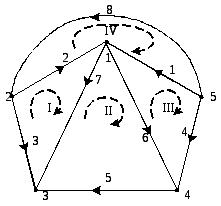
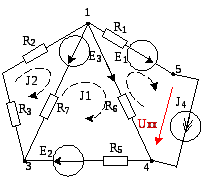
Приведем ориентированный граф схемы и составим топологические матрицы: узловую, контурную, диагональную матрицу сопротивлений, диагональную матрицу проводимостей, столбцевые матрицы ЭДС и источников тока.

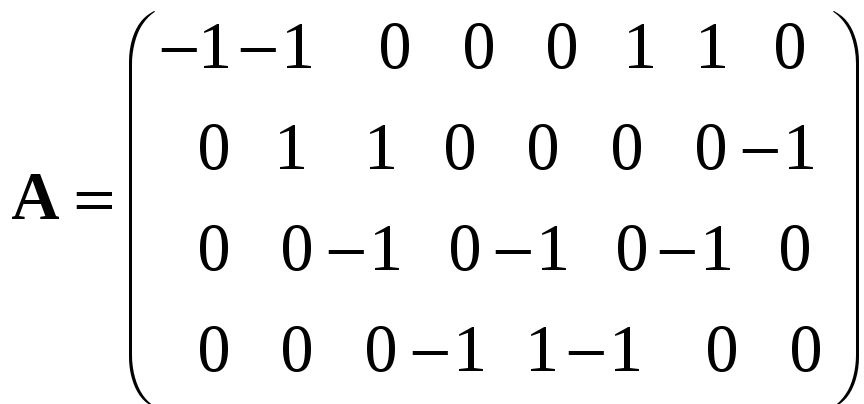
– узловая топологическая матрица,

– узловая контурная матрица,

– диагональные матрицы сопротивлений, и проводимостей соответственно.

Находим эквивалентную матрицу ЭДС, так как присутствуют источники тока

.

Находим контурные токи:

.

Находим токи в ветвях:

.

• Выполняем второй пункт задания

Находим потенциалы узлов с помощью топологической узловой матрицы:

.

Находим напряжения на ветвях:

.

Определяем токи в ветвях:

.

• Выполняем третий пункт задания

Проверяем баланс мощностей:

– мощность источников.

– мощность потребителей.

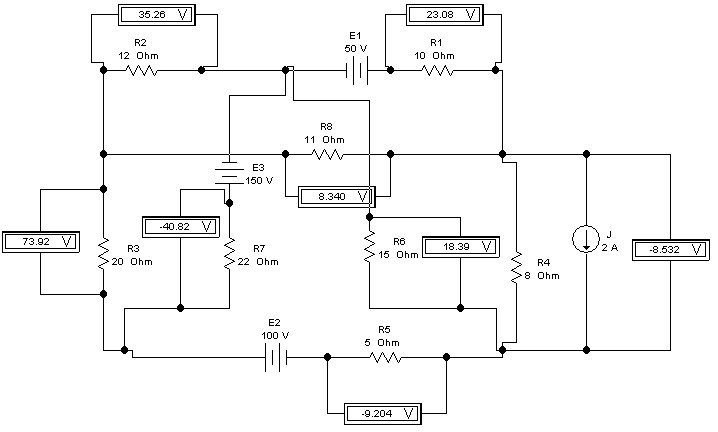
• Выполняем четвертый пункт задания

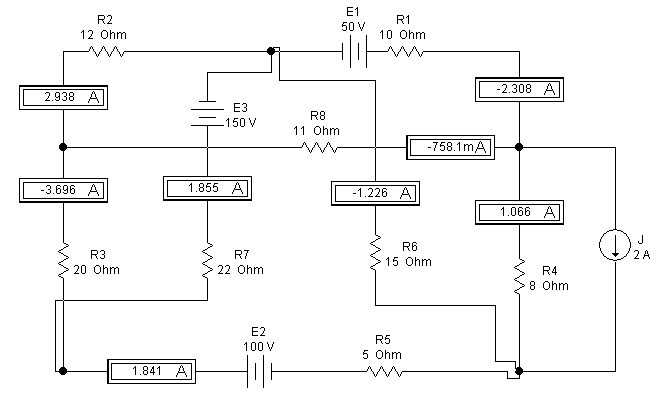
Рис. Схема, собранная в Electronics Workbench. Схема измерения токов ветвей

Проделав виртуальный эксперимент, мы получили токи в ветвях с точность до четвертой значащей цифры.

Рис. На схеме приведено измерения напряжения на сопротивлениях схемы.

Следующим этапом, измеряем, напряжения на сопротивлениях схемы и получаем величины напряжений не отличающиеся от расчетных (см. схему).

• Выполняем пятый пункт задания

Рисуем схему без сопротивления _. Рассчитаем ток в ветви с сопротивлением R₄ методом эквивалентного генератора. Построим выходную характеристику генератора и график зависимости мощности от тока P(I) и сопротивления нагрузки P(R_н)

Находим напряжение холостого хода . Для этого убираем сопротивление и находим токи в ветвях.

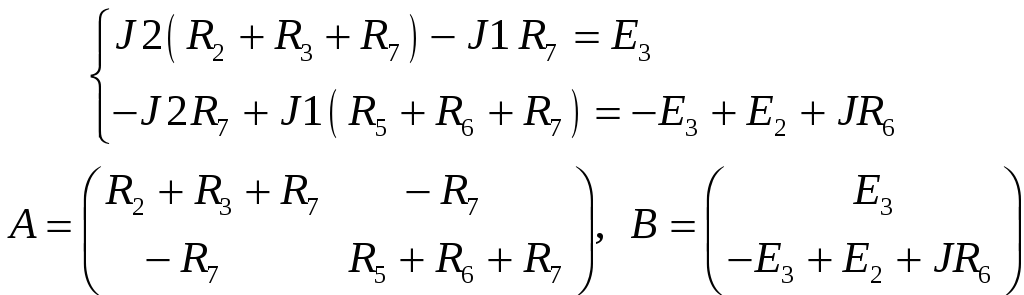
Подставим числовые значения и получим

Находим напряжение холостого хода в соответствии со схемой:

Находим сопротивление генератора:

Находим ток короткого замыкания и в четвертой ветви:

Строим выходную характеристику эквивалентного генератора. . По оси напряжений откладываем напряжение , а по оси токов ток короткого замыкания , соединяя отложенные точки, получаем выходную характеристику.

Рис Выходная характеристика генератора

Строим вольтамперную характеристику (ВАХ) сопротивления ветви . Для этого величину сопротивления умножаем на произвольную величину тока, например на и получаем точку на плоскости . Соединяем точку с началом координат (см. рис) и получаем ВАХ. Точка пересечения выходной и вольтамперной характеристик дает нам ток и напряжения сопротивления , , .

Строим зависимость мощности от сопротивления нагрузки :

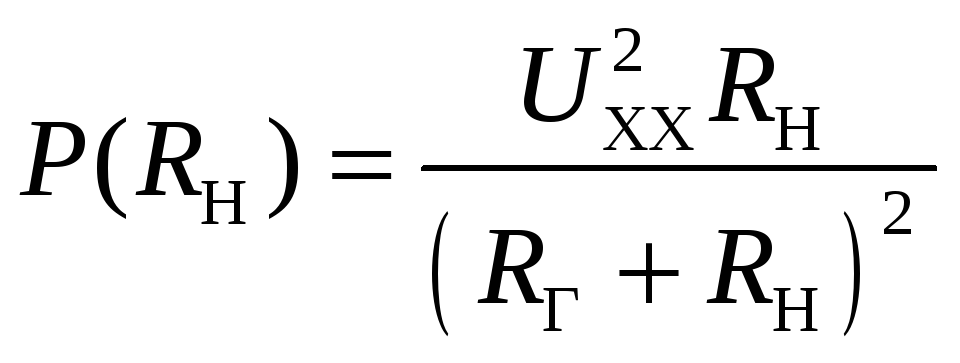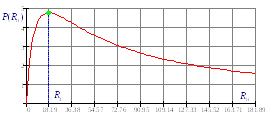
Рис. Мощность генератора в зависимости от нагрузки

Здесь нужно обратить внимание, что максимум мощности приходится на величину нагрузки равной сопротивлению генератора .

Рис. Мощность нагрузки в зависимости от тока нагрузки

С троим зависимость мощности от сопротивления нагрузки:

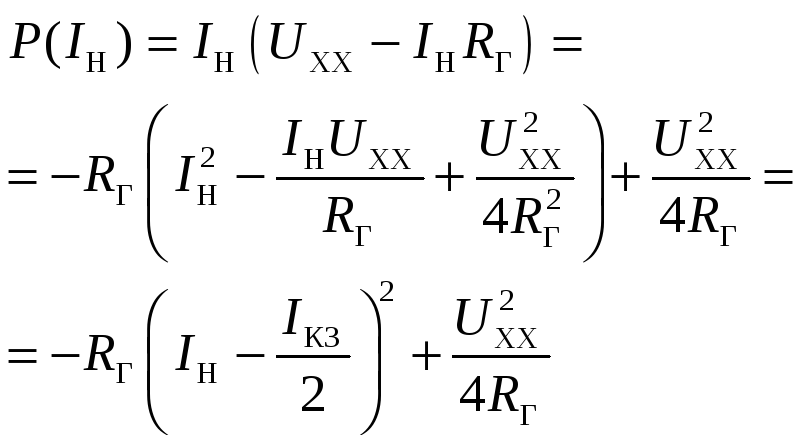
Максимальная мощность приходится на величину половине тока короткого замыкания :

.

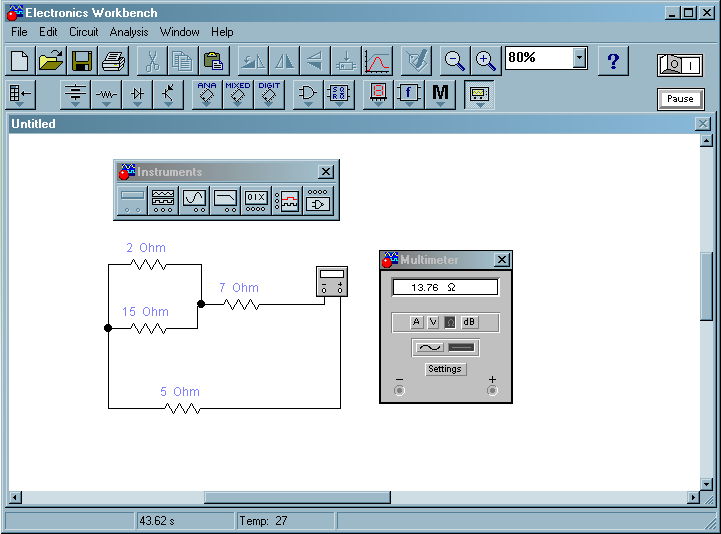
В завершении проверим все вычисления, проделав виртуальную лабораторную работу в Electronics Workbench.

Подключение мультиметра.

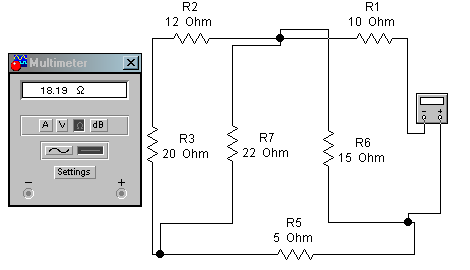
Рис . Мультиметр работает в режиме омметра и измеряет сопротивление генератора

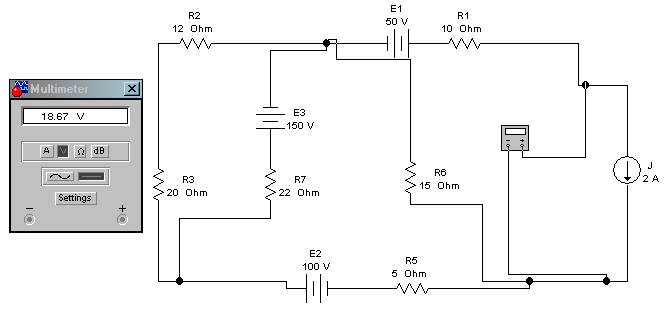
Рис. Мультиметр работает в режиме вольтметра и измеряет напряжение холостого хода.

Лекция № 5