- •Линейные электрические цепи
- •Постоянный ток
- •§ 1.1. Законы Кирхгофа
- •§ 1.2. Примеры использования законов Кирхгофа (методы расчетов)
- •§ 1.3. Матрично-топологический метод
- •§ 1.4. Метод контурных токов
- •§ 1.5 Баланс мощностей
- •§ 1.6. Метод контурных токов на основе матрично–топологического подхода
- •§ 1.7. Метод узловых потенциалов
- •§ 1.8. Метод узловых потенциалов на основе матрично-топологического метода
- •§ 1.9. Метод эквивалентных преобразований
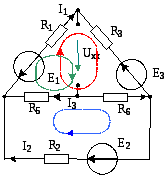
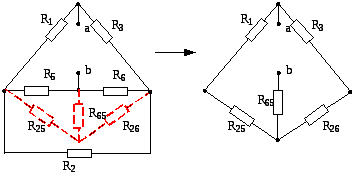
- •§ 1.10. Преобразование треугольника в звезду и звезды в треугольник
- •§ 1.11. Метод эквивалентного генератора
- •§ 1.12 Характеристики эквивалентного генератора
- •§ 1.13. Метод наложения (метод суперпозиции).
- •Варианты расчетно–графических работ по расчету цепей постоянного тока
- •Пример выполнения расчетно-графичекой работы
- •Переменный ток
- •§2.1. Немного о комплексных числах
- •§2.3. Векторные диаграммы – фазовые соотношения между величинами
- •§2.4. Показания приборов
- •§2.5. Мощность в цепи переменного тока
- •§2.6. Цепи с индуктивно связанными элементами Последовательное соединение катушек с индуктивной связью.
- •§2.7. Построение диаграммы при встречном и согласном включениях индуктивностей с магнитной связью
- •§2.8. Расчет цепи с магнитно-связанными индуктивностями
- •§2.9. Построение векторной диаграммы
- •Мощность в цепи переменного тока с взаимной индуктивностью
- •§2.10. Трансформатор
- •§2.11. Резонанс напряжений
- •Ргр №2 Расчет линейной цепи синусоидального тока
- •Трехфазные цепи
- •§3.1 Метод симметричных составляющих
- •Переходные процессы §4.1 Переходные процессы в простейших цепях. Нулевые начальные условия
- •§4.2 Классический метод расчета переходного процесса. Первый и второй законы коммутации. Понятия о зависимых и независимых начальных условиях
- •§4.3 Метод расчета переходных процессов в цепи переменный тока
- •§4.4 Переходные процессы в цепи второго порядка
- •§4.5 Операторный метод расчёта переходных процессов
- •§4.6 Интеграл Дюамеля
- •Дельта функция Дирака и -ступенчатая функция Хевисайда
- •1.3. Импульсная переходная функции (весовая функция-функция Грина)
- •§4.6 Метод пространство состояний
- •Ргр №3 расчет переходных процессов в линейных цепях Цепь I-го порядка
- •Цепь II-го порядка
- •Схемы цепей I-го порядка
- •Схемы цепей II-го порядка
- •Операционные усилители
- •§2.3 Общее рассмотрение каскада на операционном усилителе с отрицательной обратной связью
- •Контрольная работа-№1
- •Линии с распределенными параметрами
- •§5.1 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в начале линии
- •§5.2 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии
- •§5.3 Линии без потерь
- •§5.4 Коэффициент отражения
- •§5.5 Действующие значения напряжения и тока вдоль линии без потерь
- •§5.6 Стоячие волны
- •§5.7 Входное сопротивление линии без потерь при холостом ходе
- •§5.8 Аналогия между уравнениями линии с распределенными параметрами и уравнениями четырехполюсника
- •Нелинейные резистивные цепи постоянного тока
- •§6.1 Линеаризация нелинейной характеристики
- •§6.2 Расчет магнитных цепей
§ 1.11. Метод эквивалентного генератора
В ряде случаев возникает необходимость
найти ток в отдельно взятой ветви
электрической цепи. В этом случае нет
необходимости использовать громоздкие
методы расчетов определения токов во
всех ветвях. В таких случаях следует
использовать метод эквивалентного
генератора (МЭГ). МЭГ хорош еще и тем,
что позволяет определить сопротивление
нагрузки двухполюсника, при котором
выделяется максимальная мощность, что
очень важно при последовательном
включении каскадов, согласованных по
мощности. Иногда этот метод называют
методом холостого хода и короткого
замыкания. Суть метода заключается
в том, что в схеме выделяется ветвь, в
которой нужно найти ток, а вся оставшаяся
часть схемы заменяется активным
двухполюсник – эквивалентный генератор.
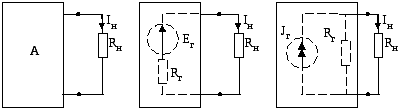
Существуют две схемы замещения активного
двухполюсника (см рис 20.): 1-двухполюсник
состоит из источника напряжения, ЭДС –
![]() и сопротивления
и сопротивления
![]() .
2- двухполюсник состоит из источника
тока –
.
2- двухполюсник состоит из источника
тока –![]() и
проводимости
и
проводимости
![]() .
.
|
Рис. 20 Схема замещения эквивалентного генератора |
Чтобы определить ЭДС генератора
![]() ,
следует найти напряжение холостого
хода–
,
следует найти напряжение холостого
хода–![]() относительно выходных зажимов
эквивалентного генератора, это и будет
искомая ЭДС. Для того чтобы найти
сопротивление генератора
относительно выходных зажимов
эквивалентного генератора, это и будет
искомая ЭДС. Для того чтобы найти
сопротивление генератора
![]() ,
следует найти сопротивление относительно
выходных зажимов генератора. После
определения
,
следует найти сопротивление относительно
выходных зажимов генератора. После
определения
![]() и
и
![]() легко найти ток короткого замыкания –
легко найти ток короткого замыкания –
![]() .
Источник тока эквивалентного генератора–
.
Источник тока эквивалентного генератора–![]() равен току короткого замыкания
равен току короткого замыкания
![]() .
При известных параметрах эквивалентного
генератора можно найти ток в нагрузке:
.
При известных параметрах эквивалентного
генератора можно найти ток в нагрузке:
![]() . (44)
. (44)
Если известен ток короткого замыкания
![]() ,
применив правило разброса легко найти
ток в нагрузке, используя соотношение:
,
применив правило разброса легко найти
ток в нагрузке, используя соотношение:
|
Рис. 21 |
Для более глубокого понимания целесообразно рассмотреть пример.
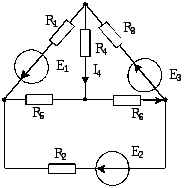
Пример 4: Даны сопротивления и ЭДС:
![]()
Определить ток
![]() в четвёртой ветви, используя метод
эквивалентного генератора.
в четвёртой ветви, используя метод
эквивалентного генератора.
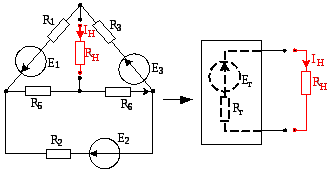
Решение: Прежде всего, необходимо
преобразовать схему в двухполюсник:
выделяем ветвь с сопротивлением
![]() ,
а всю оставшуюся часть заменяем
двухполюсником – эквивалентным
генератором. Затем находим напряжение
холостого хода и сопротивление
эквивалентного генератора.
,
а всю оставшуюся часть заменяем
двухполюсником – эквивалентным
генератором. Затем находим напряжение
холостого хода и сопротивление
эквивалентного генератора.
|
|
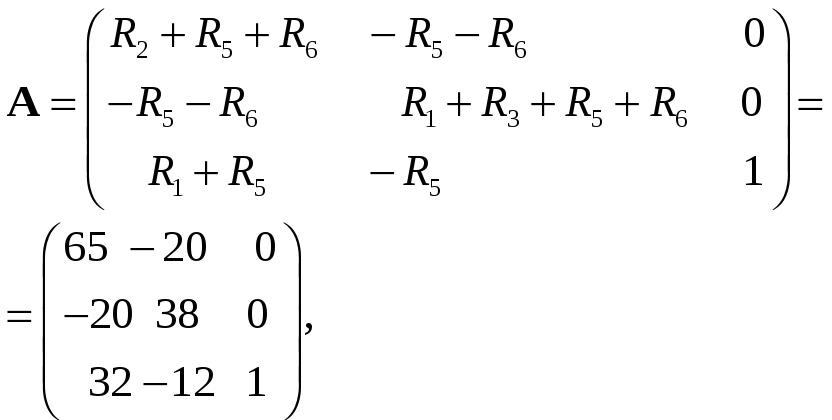
|
Рис 23 |
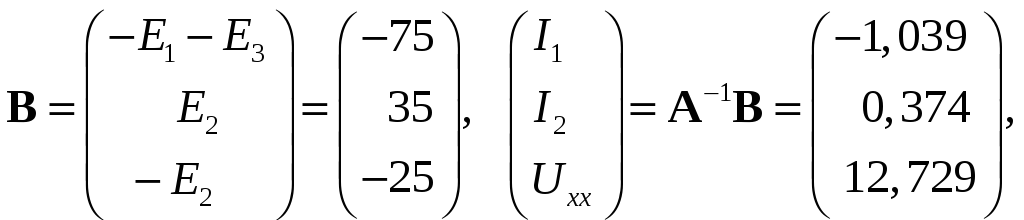
Таким образом имеем напряжение холостого
хода
![]()
|
Рис. 24 |
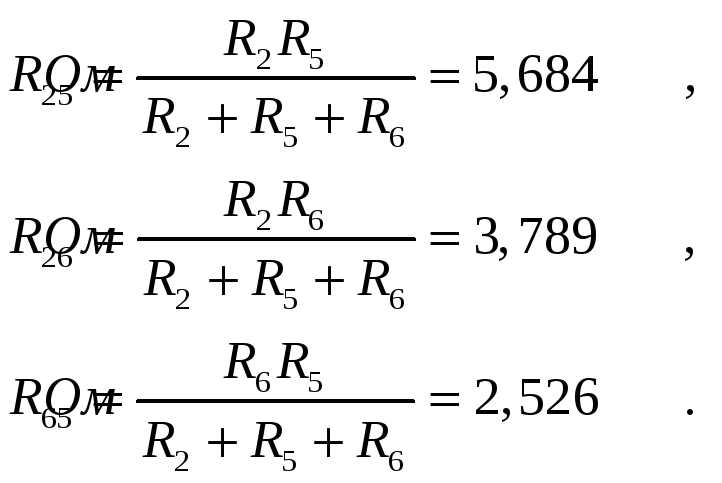
![]()
В соответствии со схемой эквивалентного
генератора находим ток короткого
замыкания и ток в 4-той ветви
![]()
![]()
Mathcad (характеристики генератора)
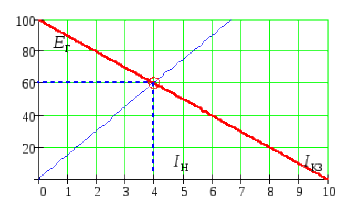
§ 1.12 Характеристики эквивалентного генератора
Важной характеристикой эквивалентного генератора является
1. Выходная характеристика ![]() :
:
|
Рис 23 |
На этой зависимости ток изменяется в
пределах
![]() ,
а напряжение в пределах
,
а напряжение в пределах
![]() ,
,
![]() .
Выходная характеристика хороша тем,
что позволяет определить ток нагрузки
.
Выходная характеристика хороша тем,
что позволяет определить ток нагрузки
![]() при любой величине сопротивления
заданной нагрузки
при любой величине сопротивления
заданной нагрузки
![]() .
Для того чтобы определить ток нагрузки
.
Для того чтобы определить ток нагрузки
![]() ,
достаточно умножить произвольное
значение тока на величину сопротивления
нагрузки
,
достаточно умножить произвольное
значение тока на величину сопротивления
нагрузки
![]() (см. рис.), затем отложить найденное
значение на графике и соединить с началом
координат (на графике это сделано для
нагрузки
(см. рис.), затем отложить найденное
значение на графике и соединить с началом
координат (на графике это сделано для
нагрузки
![]() ). Опустив перпендикуляр с точки
пересечения полученной кривой и выходной
характеристики на ось токов, мы получаем
значение интересующего нас тока. В нашем
случае
). Опустив перпендикуляр с точки
пересечения полученной кривой и выходной
характеристики на ось токов, мы получаем
значение интересующего нас тока. В нашем
случае
![]() .
.
Еще несколько важных характеристик
генератора - мощность нагрузки
![]() ,
в зависимости от величины нагрузки, и
мощность нагрузки
,
в зависимости от величины нагрузки, и
мощность нагрузки
![]() в
зависимости от величины тока нагрузки.
в
зависимости от величины тока нагрузки.
-
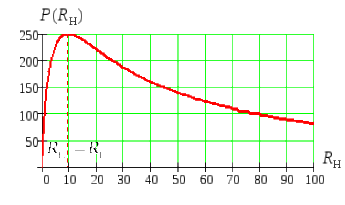
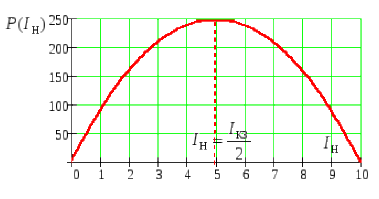
Определим мощность в нагрузке как функцию сопротивления нагрузки
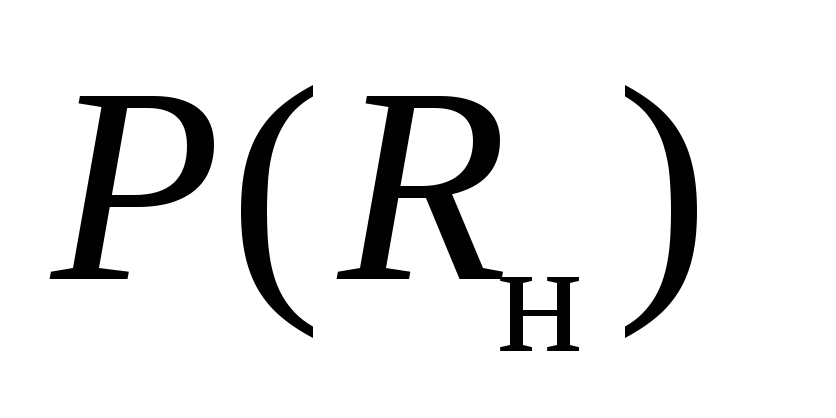 .
.
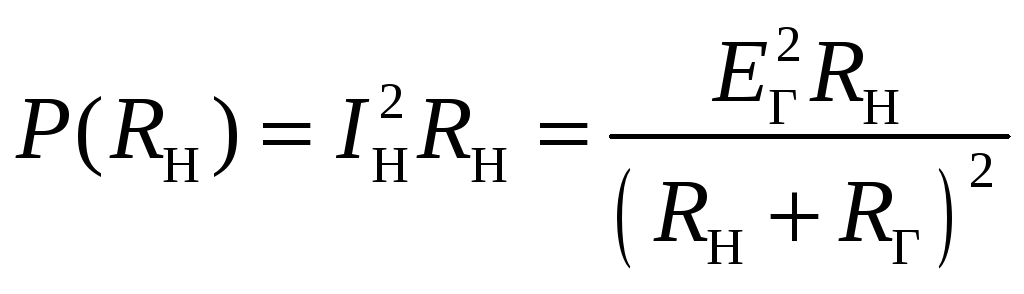 .
.
|
Рис 24. Зависимость мощности от нагрузочного сопротивления |
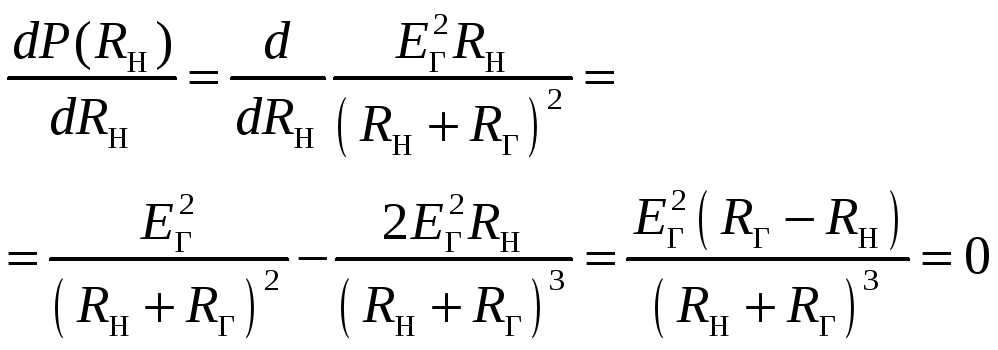 .
.
Из последнего выражения следует, что
для выделения максимальной мощности
необходимо выполнение условия
![]() .
.
-
Определим мощность в нагрузке как функцию тока нагрузки
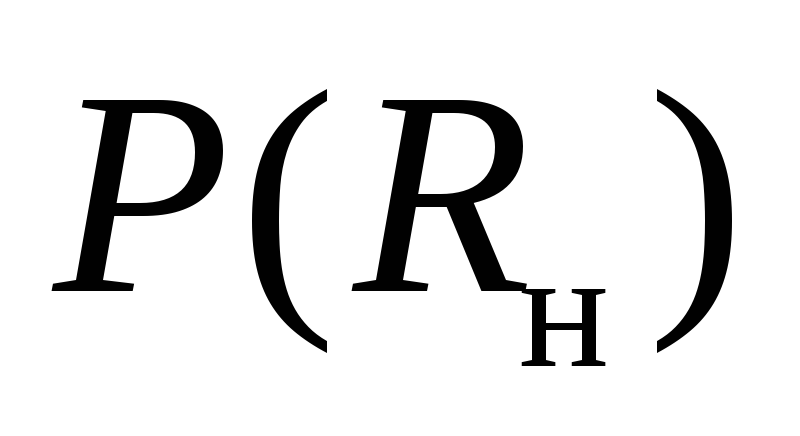 .
После несложных преобразований получаем:
.
После несложных преобразований получаем:
![]() .
.
Дополняя это выражение до полного квадрата, получаем:
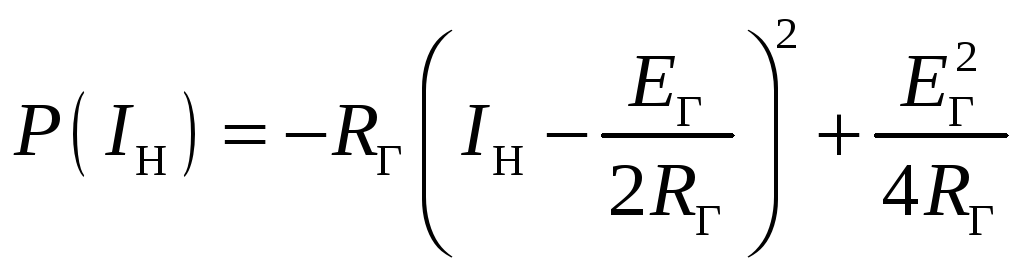
|
Рис 25. Зависимость мощности от тока нагрузки |

 Рис
22
Рис
22