
- •Линейные электрические цепи
- •Постоянный ток
- •§ 1.1. Законы Кирхгофа
- •§ 1.2. Примеры использования законов Кирхгофа (методы расчетов)
- •§ 1.3. Матрично-топологический метод
- •§ 1.4. Метод контурных токов
- •§ 1.5 Баланс мощностей
- •§ 1.6. Метод контурных токов на основе матрично–топологического подхода
- •§ 1.7. Метод узловых потенциалов
- •§ 1.8. Метод узловых потенциалов на основе матрично-топологического метода
- •§ 1.9. Метод эквивалентных преобразований
- •§ 1.10. Преобразование треугольника в звезду и звезды в треугольник
- •§ 1.11. Метод эквивалентного генератора
- •§ 1.12 Характеристики эквивалентного генератора
- •§ 1.13. Метод наложения (метод суперпозиции).
- •Варианты расчетно–графических работ по расчету цепей постоянного тока
- •Пример выполнения расчетно-графичекой работы
- •Переменный ток
- •§2.1. Немного о комплексных числах
- •§2.3. Векторные диаграммы – фазовые соотношения между величинами
- •§2.4. Показания приборов
- •§2.5. Мощность в цепи переменного тока
- •§2.6. Цепи с индуктивно связанными элементами Последовательное соединение катушек с индуктивной связью.
- •§2.7. Построение диаграммы при встречном и согласном включениях индуктивностей с магнитной связью
- •§2.8. Расчет цепи с магнитно-связанными индуктивностями
- •§2.9. Построение векторной диаграммы
- •Мощность в цепи переменного тока с взаимной индуктивностью
- •§2.10. Трансформатор
- •§2.11. Резонанс напряжений
- •Ргр №2 Расчет линейной цепи синусоидального тока
- •Трехфазные цепи
- •§3.1 Метод симметричных составляющих
- •Переходные процессы §4.1 Переходные процессы в простейших цепях. Нулевые начальные условия
- •§4.2 Классический метод расчета переходного процесса. Первый и второй законы коммутации. Понятия о зависимых и независимых начальных условиях
- •§4.3 Метод расчета переходных процессов в цепи переменный тока
- •§4.4 Переходные процессы в цепи второго порядка
- •§4.5 Операторный метод расчёта переходных процессов
- •§4.6 Интеграл Дюамеля
- •Дельта функция Дирака и -ступенчатая функция Хевисайда
- •1.3. Импульсная переходная функции (весовая функция-функция Грина)
- •§4.6 Метод пространство состояний
- •Ргр №3 расчет переходных процессов в линейных цепях Цепь I-го порядка
- •Цепь II-го порядка
- •Схемы цепей I-го порядка
- •Схемы цепей II-го порядка
- •Операционные усилители
- •§2.3 Общее рассмотрение каскада на операционном усилителе с отрицательной обратной связью
- •Контрольная работа-№1
- •Линии с распределенными параметрами
- •§5.1 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в начале линии
- •§5.2 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии
- •§5.3 Линии без потерь
- •§5.4 Коэффициент отражения
- •§5.5 Действующие значения напряжения и тока вдоль линии без потерь
- •§5.6 Стоячие волны
- •§5.7 Входное сопротивление линии без потерь при холостом ходе
- •§5.8 Аналогия между уравнениями линии с распределенными параметрами и уравнениями четырехполюсника
- •Нелинейные резистивные цепи постоянного тока
- •§6.1 Линеаризация нелинейной характеристики
- •§6.2 Расчет магнитных цепей
§ 1.4. Метод контурных токов
|
|
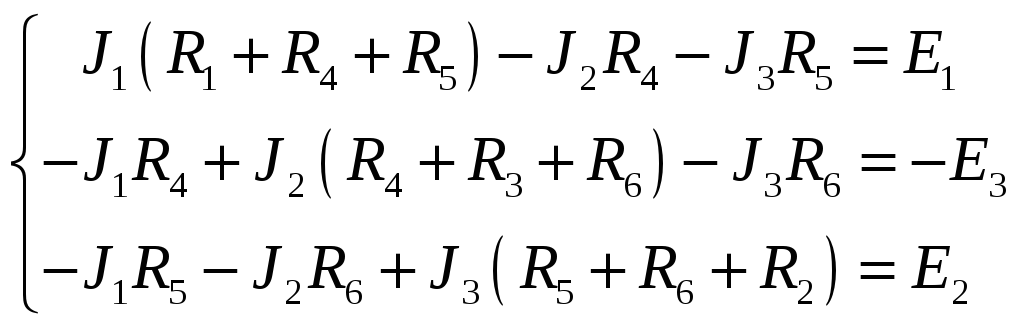 . (19)
. (19)
При составлении уравнений учтено, что в смежных ветвях протекают два контурных тока, направленных навстречу друг другу. Подставляем числовые значения сопротивлений и ЭДС в СЛАУ и получаем решения:
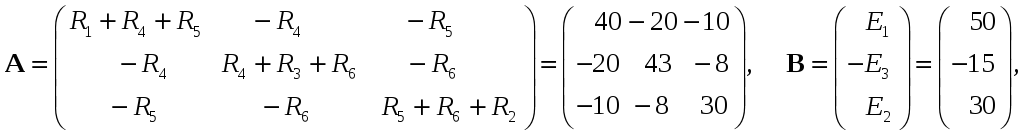
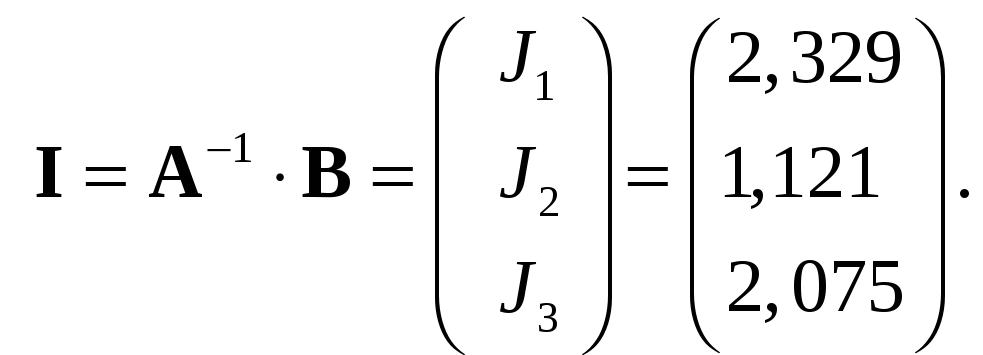 (20)
(20)
Теперь можно найти токи в ветвях, используя их связь с контурными токами:
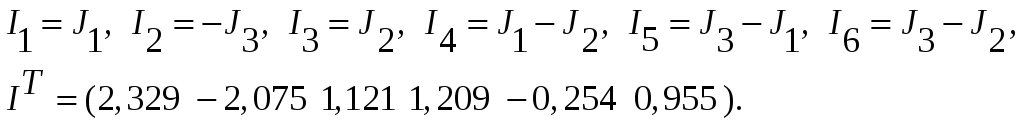 (21)
(21)
§ 1.5 Баланс мощностей
При составлении СЛАУ по первому и второму законам Кирхгофа можно допустить ошибку, например, пропустить в нужном месте знак минус, и, как следствие, получить неправильное значение токов. Для проверки числовых значений токов составляют баланс мощностей для источников энергии – ЭДС и источников тока, и для потребителей энергии – сопротивлений. Это закон сохранения энергии – сколько энергии было выделено источниками энергии – столько же должно быть потреблено потребителями. Определим мощность источников и мощность приёмников для нашей схемы.
Мощность источников энергии:
![]() (22)
(22)
Мощность потребителей энергии:
![]() (23)
(23)
Баланс сошелся, следовательно, все токи найдены правильно.
§ 1.6. Метод контурных токов на основе матрично–топологического подхода
Теперь решим задачу примера 1 матрично–топологическим методом. Топологический метод заключается в формализации всех операций. Для этого нам понадобятся топологическая контурная матрица и диагональная матрица сопротивлений:
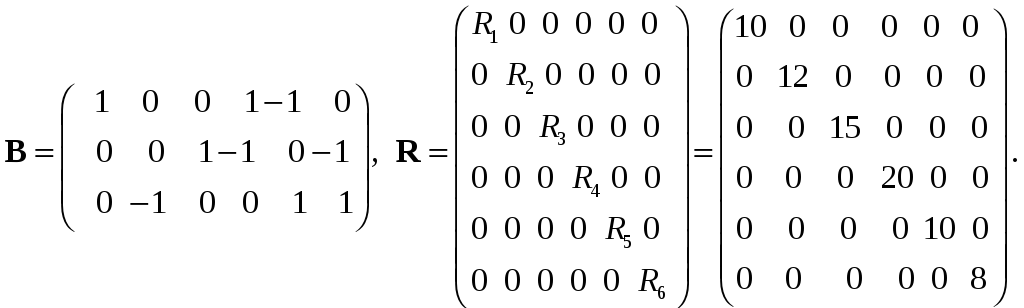 (24)
(24)
Матрицу сопротивлений для контуров можно переписать в виде матричного произведения трех топологических матриц:
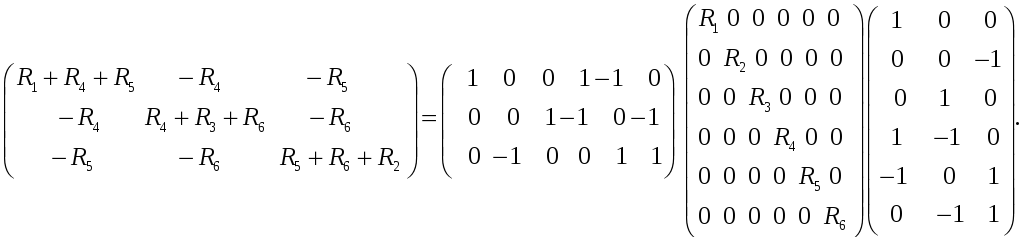
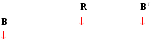
М атрицу
вектора правых частей тоже можно записать
в виде произведения топологических
матриц
атрицу
вектора правых частей тоже можно записать
в виде произведения топологических
матриц
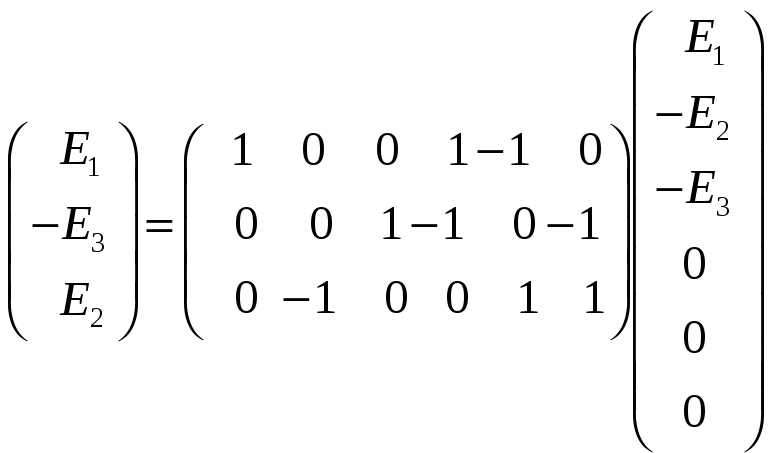 .
.
И![]() ,
наконец, контурные токи можно выразить
через токи в ветвях, используя
топологические матрицы
,
наконец, контурные токи можно выразить
через токи в ветвях, используя
топологические матрицы

Следовательно, можно формализовать метод контурных токов, используя топологические матрицы. Последовательность действий такова:
записываем произведение матриц:
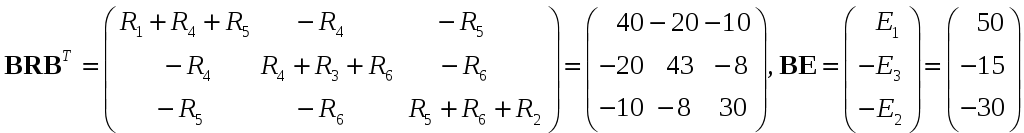 ,
(25)
,
(25)
находим контурные токи, а затем и токи в ветвях:
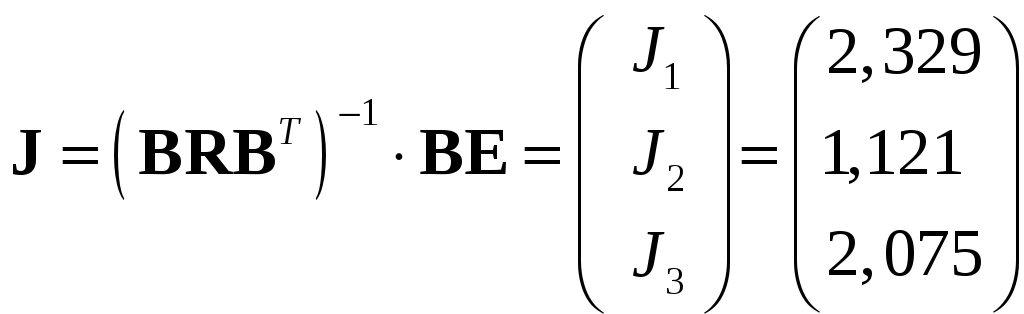 .
(26)
.
(26)
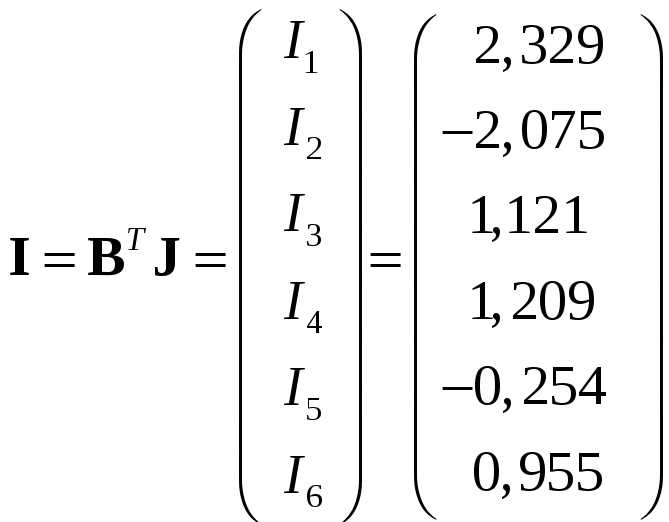 .
(27)
.
(27)
Проверим результат решения, проделав виртуальную лабораторную работу с помощью программы Electronics Workbench. Измерим токи в ветвях, подключив амперметры последовательно с сопротивлениями. Листинг программы Electronics Workbench, представленный на рисунке, свидетельствует о правильном расчете.
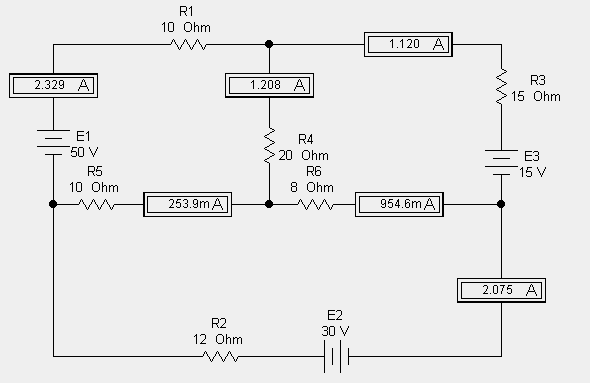
Рис 11. Схема, собранная в Electronics Workbench.
§ 1.7. Метод узловых потенциалов
|
Рис. 12 |
Прежде всего, запишем систему уравнений относительно токов по первому закону Кирхгофа.
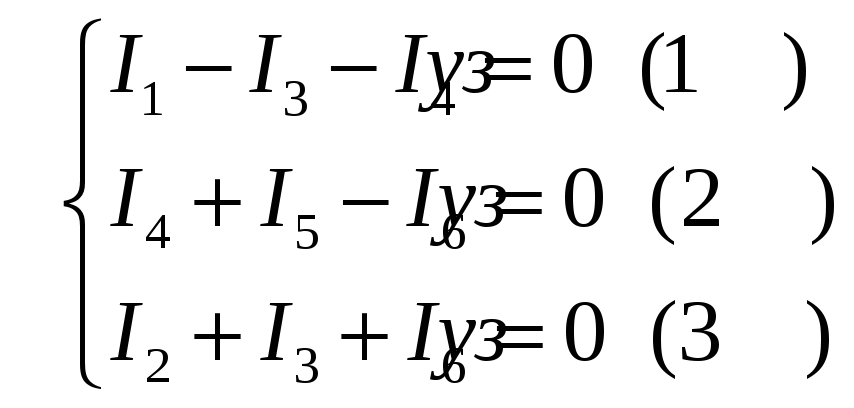
Теперь запишем токи через неизвестные значения потенциалов и известные значения ЕДС и сопротивлений.
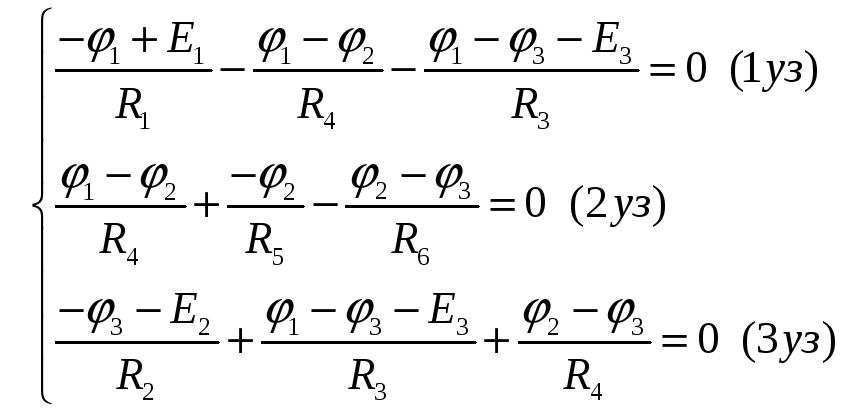
Сгруппируем эти уравнения относительно
неизвестных
![]() и в результате получаем
и в результате получаем
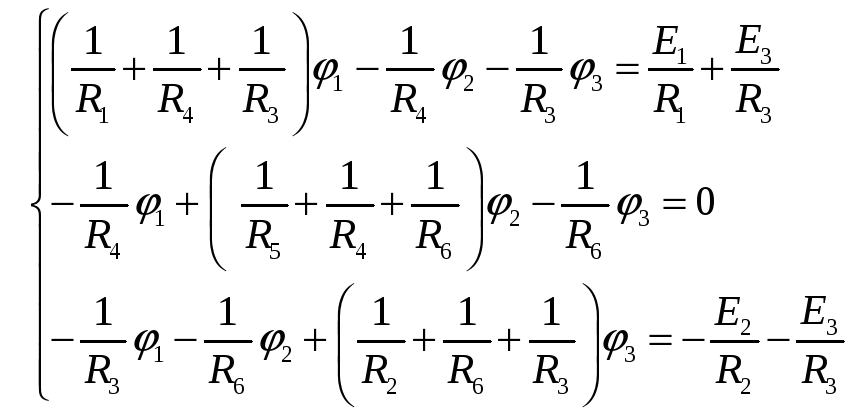
Сумма проводимостей ветвей, подходящих к узлу, называется собственной проводимостью узла. Например, для узлов 1, 2 и 3 это будет соответственно:

или в матричном виде:
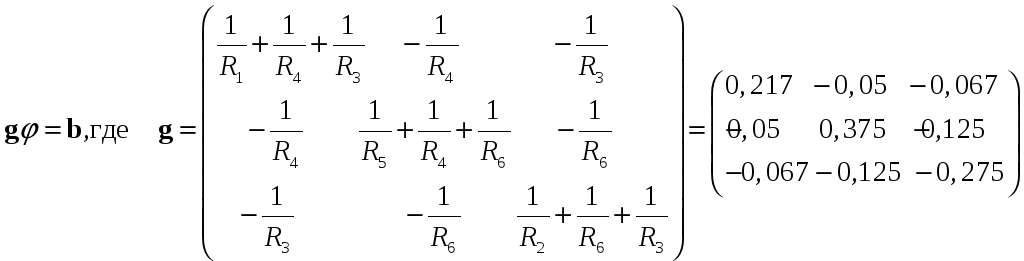 ,
(29)
,
(29)
а
![]() –
столбцевая матрица правых частей
–
столбцевая матрица правых частей
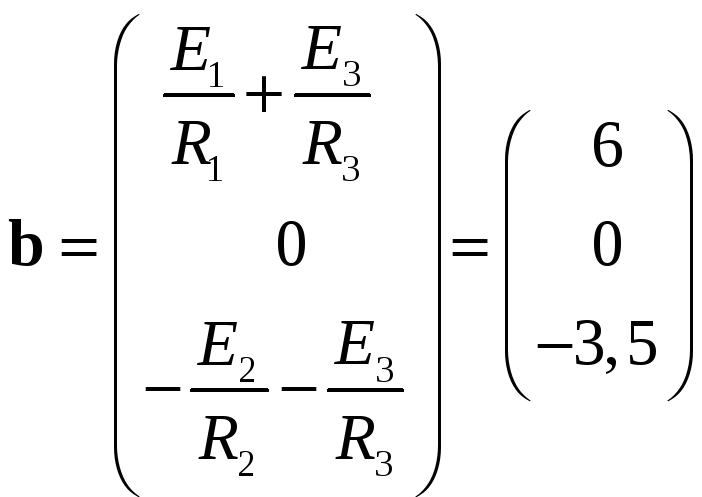 . (30)
. (30)
Решая систему уравнений (29), получаем потенциалы узлов:
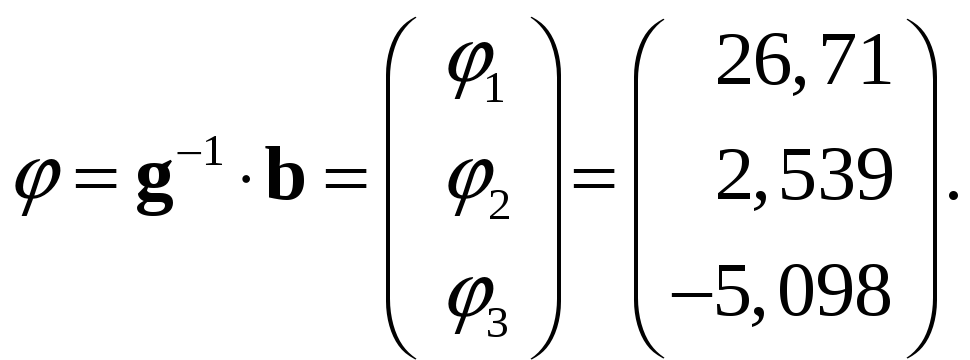 (31)
(31)
И, наконец, находим токи во всех ветвях:
 (32)
(32)

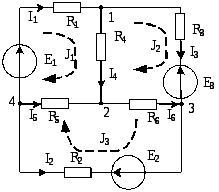 Рис. 10
Рис. 10