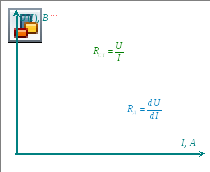
- •Линейные электрические цепи
- •Постоянный ток
- •§ 1.1. Законы Кирхгофа
- •§ 1.2. Примеры использования законов Кирхгофа (методы расчетов)
- •§ 1.3. Матрично-топологический метод
- •§ 1.4. Метод контурных токов
- •§ 1.5 Баланс мощностей
- •§ 1.6. Метод контурных токов на основе матрично–топологического подхода
- •§ 1.7. Метод узловых потенциалов
- •§ 1.8. Метод узловых потенциалов на основе матрично-топологического метода
- •§ 1.9. Метод эквивалентных преобразований
- •§ 1.10. Преобразование треугольника в звезду и звезды в треугольник
- •§ 1.11. Метод эквивалентного генератора
- •§ 1.12 Характеристики эквивалентного генератора
- •§ 1.13. Метод наложения (метод суперпозиции).
- •Варианты расчетно–графических работ по расчету цепей постоянного тока
- •Пример выполнения расчетно-графичекой работы
- •Переменный ток
- •§2.1. Немного о комплексных числах
- •§2.3. Векторные диаграммы – фазовые соотношения между величинами
- •§2.4. Показания приборов
- •§2.5. Мощность в цепи переменного тока
- •§2.6. Цепи с индуктивно связанными элементами Последовательное соединение катушек с индуктивной связью.
- •§2.7. Построение диаграммы при встречном и согласном включениях индуктивностей с магнитной связью
- •§2.8. Расчет цепи с магнитно-связанными индуктивностями
- •§2.9. Построение векторной диаграммы
- •Мощность в цепи переменного тока с взаимной индуктивностью
- •§2.10. Трансформатор
- •§2.11. Резонанс напряжений
- •Ргр №2 Расчет линейной цепи синусоидального тока
- •Трехфазные цепи
- •§3.1 Метод симметричных составляющих
- •Переходные процессы §4.1 Переходные процессы в простейших цепях. Нулевые начальные условия
- •§4.2 Классический метод расчета переходного процесса. Первый и второй законы коммутации. Понятия о зависимых и независимых начальных условиях
- •§4.3 Метод расчета переходных процессов в цепи переменный тока
- •§4.4 Переходные процессы в цепи второго порядка
- •§4.5 Операторный метод расчёта переходных процессов
- •§4.6 Интеграл Дюамеля
- •Дельта функция Дирака и -ступенчатая функция Хевисайда
- •1.3. Импульсная переходная функции (весовая функция-функция Грина)
- •§4.6 Метод пространство состояний
- •Ргр №3 расчет переходных процессов в линейных цепях Цепь I-го порядка
- •Цепь II-го порядка
- •Схемы цепей I-го порядка
- •Схемы цепей II-го порядка
- •Операционные усилители
- •§2.3 Общее рассмотрение каскада на операционном усилителе с отрицательной обратной связью
- •Контрольная работа-№1
- •Линии с распределенными параметрами
- •§5.1 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в начале линии
- •§5.2 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии
- •§5.3 Линии без потерь
- •§5.4 Коэффициент отражения
- •§5.5 Действующие значения напряжения и тока вдоль линии без потерь
- •§5.6 Стоячие волны
- •§5.7 Входное сопротивление линии без потерь при холостом ходе
- •§5.8 Аналогия между уравнениями линии с распределенными параметрами и уравнениями четырехполюсника
- •Нелинейные резистивные цепи постоянного тока
- •§6.1 Линеаризация нелинейной характеристики
- •§6.2 Расчет магнитных цепей
§5.8 Аналогия между уравнениями линии с распределенными параметрами и уравнениями четырехполюсника
Напряжение и ток на входе линии с
распределенными параметрами
![]() связаны
с напряжением и током в конце линии
связаны
с напряжением и током в конце линии
![]() следующими
уравнениями:
следующими
уравнениями:
 .
.
Сопоставим их с известными уравнениями четырехполюсника:
 .
.
Из сопоставления следует что уравнения по форме полностью аналогичны, а если принять обозначения, что
![]() (17е)
(17е)
то зависимость между
![]() и
и
![]() ,
и
,
и
![]() и
зависимость между
и
зависимость между
![]() ,
и
,
и
![]() и
и
![]() в линиях с распределенными параметрами
Точно такие же, как в четырехполюснике.
Другими словами, при соблюдении условий
(17е) четырехполюсник эквивалентен линии
с распределенными параметрами в отношении
связи между входными и выходными токами
и напряжениями.
в линиях с распределенными параметрами
Точно такие же, как в четырехполюснике.
Другими словами, при соблюдении условий
(17е) четырехполюсник эквивалентен линии
с распределенными параметрами в отношении
связи между входными и выходными токами
и напряжениями.
При перемене местами источника и нагрузки токи в источнике и нагрузке не изменятся. Таким же свойством обладает симметричный четырехполюсник. Поэтому однородная линия с распределенными параметрами может быть заменена симметричным четырехполюсником и. наоборот, симметричный четырехполюсник можно заменить участком однородной линии с распределенными параметрами.
Т-схема П-схема


Для симметричной Т-схемы замещения четырехполюсника:
![]()
![]()
или

Для симметричной П - схемы
![]()
![]() или
или
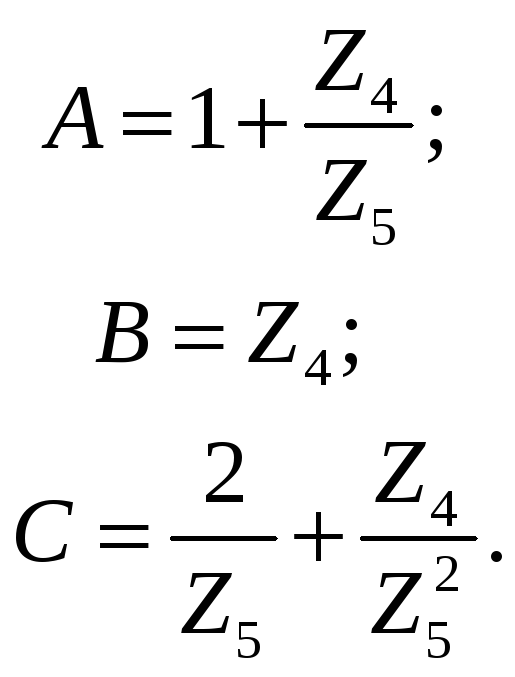
Пример: В Т-схеме четырехполюсника
![]() Определить характеристическое (волновое)
сопротивление и произведение
Определить характеристическое (волновое)
сопротивление и произведение
![]() эквивалентной ему линии с распределенными
параметрами. Р е ш е н и е:
эквивалентной ему линии с распределенными
параметрами. Р е ш е н и е:

Лекция № 14
Нелинейные резистивные цепи постоянного тока
До сих пор мы рассматривали цепи, в которых соотношения между токами и напряжения подчинялись линейным законам. Сопротивления в таких цепях были линейными. Теперь рассмотрим, как рассчитывается цепь с нелинейными элементами. Вольт амперные характеристики нелинейных резистивных элементов известны. Их всегда можно измерить. Например, пропустить ток через нелинейный элемент и измерить напряжение. Проделав серию измерений можно построить воль амперную характеристику. Вольт амперные характеристики (ВАХ) двух таких элементов изображены на графике (см. рис). К нелинейным резистивным элементам относятся: лампы накаливания, диоды, транзисторы, электронные лампы и т.д.
Рассмотрим последовательное соединение двух нелинейных элементов. В цепи все элементы соединены последовательно. Через все элементы проходит один и тот же ток. Фиксируя значения тока можно сложить напряжения и получить ВАХ эквивалентного сопротивления (См. рис.).
|
|
При параллельном соединении двух нелинейных элементов напряжение на элементах одинаковое, но токи при этом разные. Фиксируя напряжения и складывая токи можно получить ВАХ эквивалентного сопротивления (См. рис.).
|
|

При смешанном соединении проводников сначала производят параллельное преобразование проводников, а затем преобразуют последовательное соединение (см. рис).
Дифференциальным сопротивлением называется величина, определяемая соотношением:
![]() (18)
(18)
Статическим сопротивлением называется величина, определяемая соотношением:
![]() (19)
(19)
|
|
Пример:
Найти статическое и дифференциальное
сопротивления в точке,
![]() если заданна зависимость
если заданна зависимость
![]() :
:
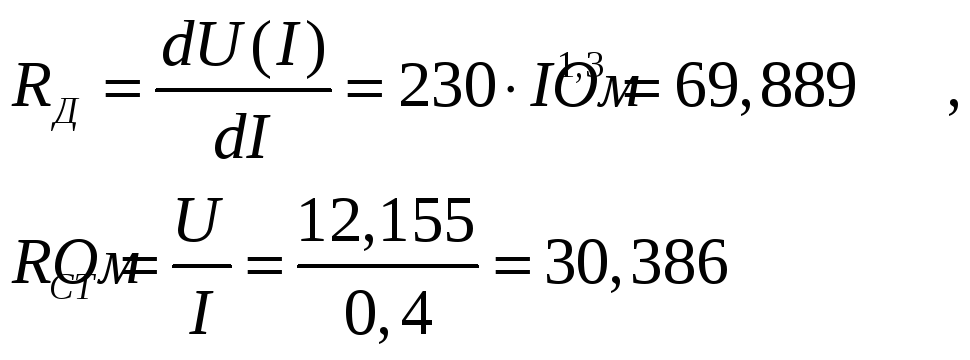
|
Дана нелинейная цепь с вольтамперной характеристикой нелинейного элемента на рисунке. Известны параметры цепи J = 4A, R = 2Ом. Определить ток I в нелинейном элементе.
|
|
Два одинаковых нелинейных элемента с известной ВАХ и сопротивление R = 133.3 Ом соединены по указанной схеме. Определить напряжение U, если известен входной ток I = 0.3 А
|
|
|
Два одинаковых
нелинейных элемента с известной
вольтамперной характеристикой и
сопротивление
|
|