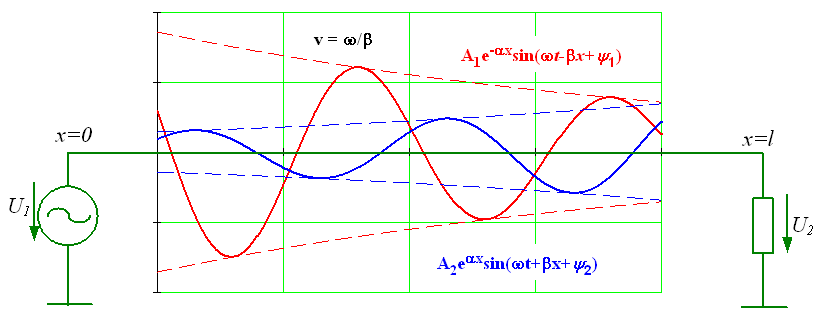
Линии с распределенными параметрами
Электрическими линиями с распределенными параметрами называются такие линии, в которых для одного и того же момента времени ток и напряжение непрерывно изменяются при переходе от одной точки (сечения) линии к другой соседней точке.
Эффект непрерывного изменения тока и напряжения вдоль линии имеет место вследствие того, что линии обладают распределенными продольными и поперечными сопротивлениями.
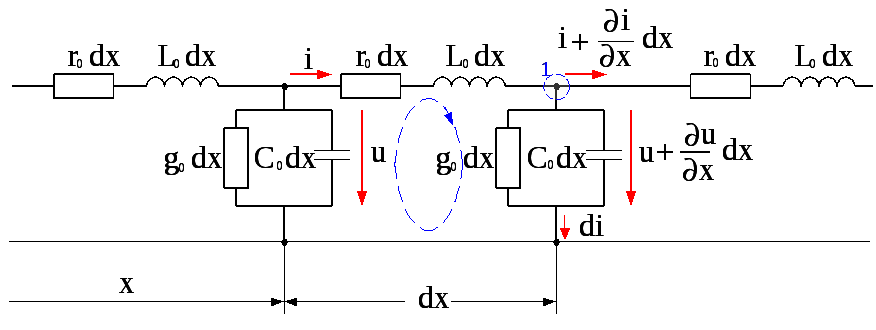
На рисунке изображен участок линии с
распределенными параметрами, через
обозначен
бесконечно малый элемент длины линии.
В результате утечки через поперечные
сопротивления токи на соседних участках
линии неодинаковы. Вследствие этого и
падение напряжения на соседних поперечных
сопротивлениях разделенных участком
тоже отличаются.
В электрических линиях с распределенными
параметрами продольные сопротивления
образованны активными сопротивлениями
проводов линии и индуктивностями двух
противостоящих друг другу участков
линии длиной
.
Поперечные сопротивления состоят из
сопротивлений утечки, появляющейся
вследствие несовершенства изоляции
между проводами линии, и емкостей,
образованных противостоящими друг
другу элементами (участками) линии.
Линию с распределенными параметрами называют однородной, если равны друг другу все продольные сопротивления участков линии одинаковой длины, и если равны друг другу все поперечные сопротивления участков линии одинаковой длины.
Линию с распределенными параметрами называют неоднородной, если продольные сопротивления в ней различны и поперечные сопротивления неодинаковы.
Когда говорят о линии с распределенными параметрами, то обычно этот термин мысленно связывают с мощными линиями передач электрической энергии на большие расстояния, с телефонными телеграфными воздушными и кабельными линиями, с антеннами в радиотехнике и другими родственными линиями и установками.
Пусть
–
продольное активное сопротивление
единицы длины линии;
–
индуктивность единицы длинны линии;
–
емкость единицы длины линии;
–поперечная
проводимость единицы длины линии (она
не является обратной величиной продольного
сопротивления
);
Разобьем линию на участки длиной
(см.
рис),
–
расстояние, отсчитываемое от начала
линии. На длине
активное сопротивление рано
,
индуктивность –
,
проводимость утечки –
и емкость –
.
И ток, и напряжение являются в общем
случае функциями расстояния вдоль линии
и времени
.
Обойдем, выделенный участок линии по контуру и запишем для него второй закон Кирхгофа - сумма падений напряжения для замкнутого контура равняется нулю:
.
Сократив на
и поделив на
получаем выражение:
.
Запишем первый закон Кирхгофа для выделенного узла –1:
(1)
Ток
равен сумме токов, проходящих через
проводимость
и емкость
:
Пренебрегая слагаемыми второго порядка малости, получим
(2)
Подставляя (2) в (1) и поделив на
,
после упрощения получаем
Таким образом, получаем систему дифференциальных уравнений в частных производных, которые в математической физике называются телеграфными уравнениями:
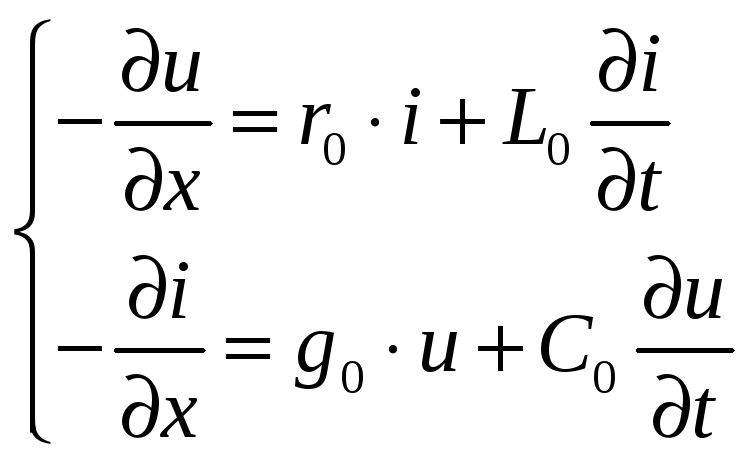(2а)
Чтобы решить эти уравнения, воспользуемся символическим методом
Введем изображения токов и напряжений
(3)
Здесь-
и
комплексные
величины тока и напряжения соответственно.
Очевидно, что в этом случае мы можем получить следующие соотношения
,
Подставив все выше полученные выражения
в телеграфные уравнения, и сократив на
множитель
,
получим
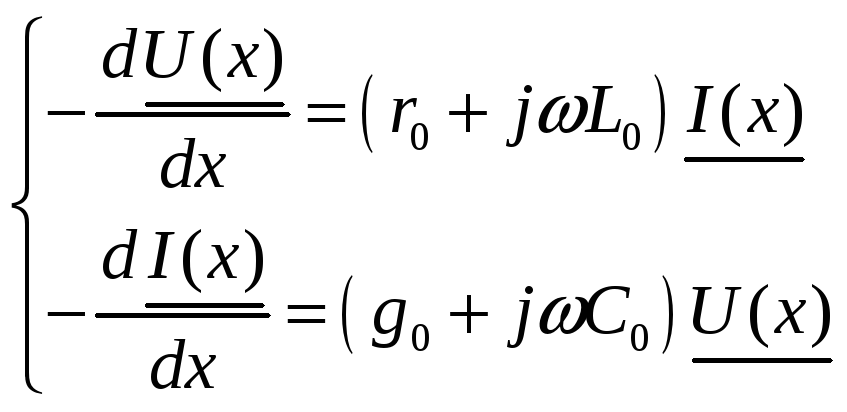(2б)
Введя обозначения
,
и опуская зависимость напряжения и тока
от пространственной координаты эти
уравнения можно переписать
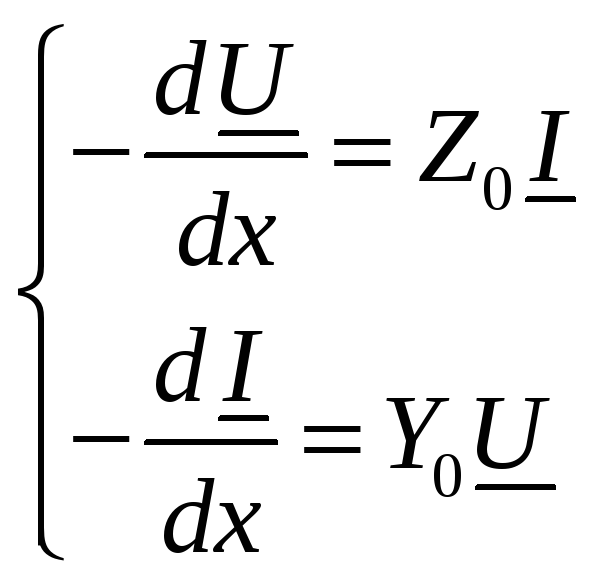(2в)
Продифференцируем первое уравнение по
и подставим в него второе получим
дифференциальное уравнение второго
порядка с постоянными коэффициентами
(2г)
Будем искать решение в виде
.
Подставляя искомое решение в (2г) получим
характеристическое уравнение относительно
.
Теперь решение можно записать в виде
.
Здесь
комплексные константы которые определяются
с помощью граничных условий, комплексное
число
принято называть постоянной
распространения. Запишем его в
алгебраической форме
,
где
–
коэффициент затухания
(характеризующий затухание падающей
волны на единицу длины линии);
– коэффициент фазы (пространственная
частота); он характеризует изменение
фазы падающей волны на единицу длины
линии. Размерность величин
.
Найдём ток из уравнений
Величину, стоящую в знаменателе
называют волновым сопротивлением
и обозначают
:
.
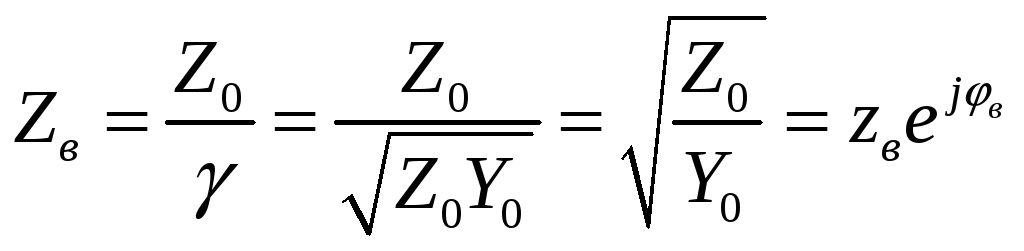Следовательно, ток можно записать
.
Теперь можно перейти от комплексных величин к мгновенным значениям, то есть осуществить обратный переход от комплексных функций к мгновенным значениям тока и напряжения:
В результате получим
|
|
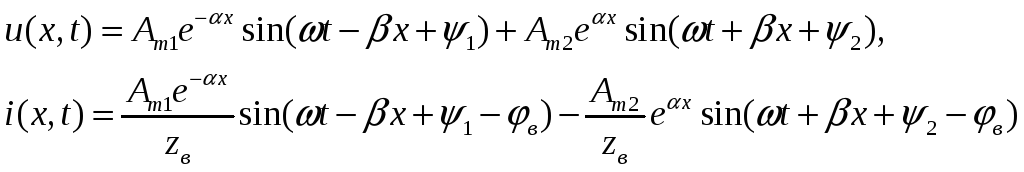
Бегущая волна характеризуется волновыми
параметрами – длинной волны
и фазовой скоростью
.
Скорость распространения –
и длину –
волны можно определить, используя
выражения:
,
.