§4.6 Метод пространство состояний

Из всех известных методов расчета переходных процессов наиболее физическим является метод пространства состояний. Этот метод позволяет одновременно получать все интересующие нас величины токов и напряжений.

Переменные состояния представляют собой систему наименьшего числа независимых величин необходимых для полного определения поведения динамической системы. Переменные состояния это токи индуктивностей и напряжения емкостей, именно они определяют состояние системы. В математической форме уравнения состояний для сложной цепи имеют вид

(8)

Сначала рассмотрим составления уравнения состояния на простейших цепях первого порядка

Определим напряжение на конденсаторе после коммутации. Вектором состояния является напряжение на емкости. Запишем второй закон Кирхгофа.

Перепишем это уравнение относительно производной

такой вид уравнения называется нормальным. Таким образом, дифференциальное уравнение, разрешенное относительно производной называется нормальным.

Рассмотрим еще один пример. Определим ток через индуктивность. В данном случае вектором состояния является ток через индуктивность. Составляем уравнение по второму закону Кирхгофа.

Разрешаем это уравнение относительно производной и получаем уравнение в нормальной форме

.

Рассмотрим пример для цепи второго порядка. Вектором состояния является переменные . Записываем уравнения по второму закону Кирхгофа, в результате получаем систему дифференциальных уравнений:

Разрешим эту систему относительно производных, то есть запишем в нормальном виде

Выпишем матрицу состояния:

.

Что бы проверить правильность составление матрицы состояния, нам нужно проверит ее собственные числа

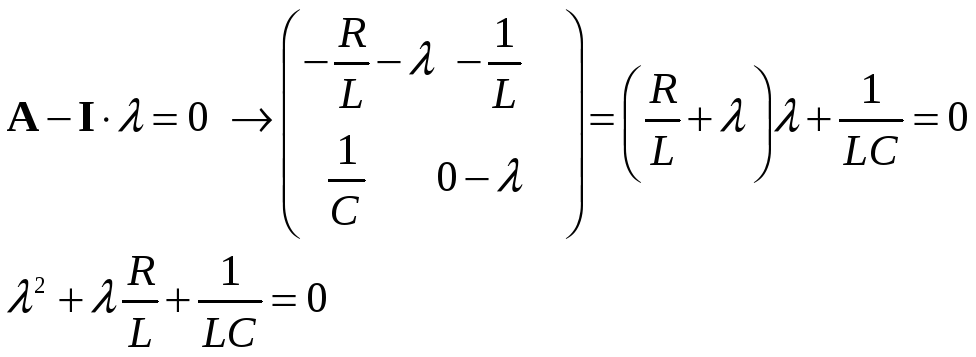
Если все сделано правильно, то это уравнение совпадает с уравнением входного сопротивления схемы

Проверим столбцевую матрицу

Результат должен дать принужденные составляющие напряжения на конденсаторе и ток через индуктивность

Рассмотрим числовой пример:

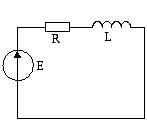
В качестве примера составим уравнение состояние для схемы приведенной на рисунке 3

Рис 3

Пример 1. Определить ток индуктивности и напряжения на ёмкостных элементах после включения ЭДС, если

Решение. Для составления уравнения состояний эффективно использовать решающие функции программно-интегрирующей среды MathCAD, такие как Given и Find. Запишем уравнения, связывающие токи и напряжение с напряжениями на ёмкостях и током индуктивности. Для этого используются первый и второй законы Кирхгофа. В нашем примере матрицы будут равны

(10)

После подстановки числовых значений получаем:

(11)

После определения матриц необходимо проверить правильность составления уравнения состояний. Это можно сделать, определив корни характеристического уравнения через сопротивление схемы:

. (12)

Корни характеристического уравнения должны полностью совпасть с собственными числами матрицы состояния  (см. рис. 4). Затем следует проверить принуждённые составляющие решений. В схеме после коммутации их легко найти, в нашем случае они определяются соотношениями:

(13)

С помощью матричных соотношений их легко проверить:

(14)

Таким образом, мы убедились, что система уравнений состояния составлена правильно.

Аналитический метод решения переходных процессов методом переменных состояния Находим матрицу состояния A, используя операции Given и Find. Составляем уравнения относительно переменных состояния Uс1, Uc2 и iL Дано: Записываем матрицу переменных состояния A и матрицу столбец правых частей BF, где B - матрица связи (размерности n x n), F-матрица столбец (размерности n x 1). Внимание!!! Произведение матриц BF здесь обозначено как B! Рис. 4. Первая страница программы MathCAD

Определяем собственные числа матрицы состояния A =>  Для проверки определяем корни характеристического уравнения через импеданс схемы Z(p) Для проверки определяем принуждённые составляющие Рис. 5. Вторая страница программы MathCAD

Теперь обращаемся к одной из стандартных процедур решения системы дифференциальных. уравнений

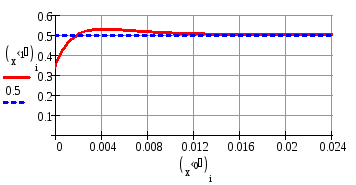
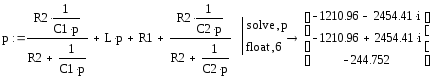
Расширенная матриц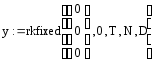а Метод Рунге Кутта