§4.5 Операторный метод расчёта переходных процессов

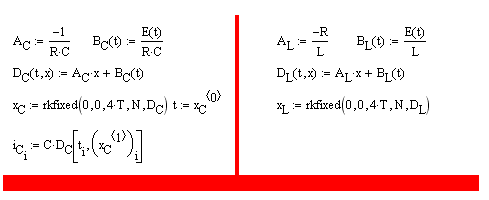
Операторный метод (преобразование Лапласа) расчета переходных процессов используется для того, чтобы обыкновенные дифференциальные уравнения с постоянными коэффициентами (в пространстве оригиналов) преобразовать в алгебраические (в пространстве изображений). Очевидно, что алгебраические уравнения решаются проще. После решения алгебраического уравнения над полученной функцией (изображением) производится обратное преобразование Лапласа, получается оригинал. Полученный оригинал – это функция, которая и будет решением дифференциального уравнения.

Любой функции можно сопоставить её преобразование Лапласа

(1)

здесь – изображение, – оригинал. Выражение (1) записывают ещё и в операторной форме.

Приведём изображение нескольких часто встречающихся функций.

Определим изображение константы – :

Найдем изображение экспоненциальной функции – :

Изображение экспоненциальной функции поможет нам найти изображения синусоидальной косинусной функций– . Для этого запишем эти функции через формулу Эйлера. Далее осуществляем следующую цепочку преобразований:

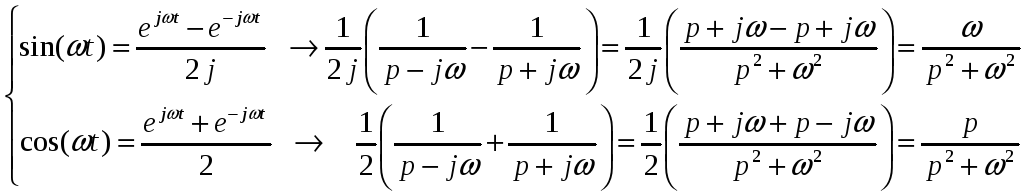
Определим изображение производной функции , имеющей изображение

И, наконец, определим изображение интегрального выражения

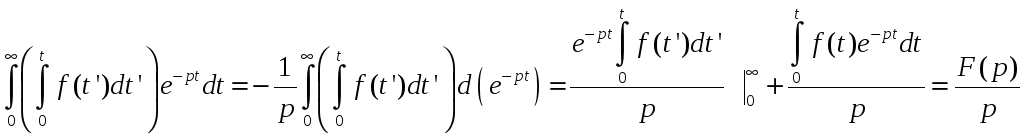
Таблица преобразований Лапласа

-оригинал	-изображение
1

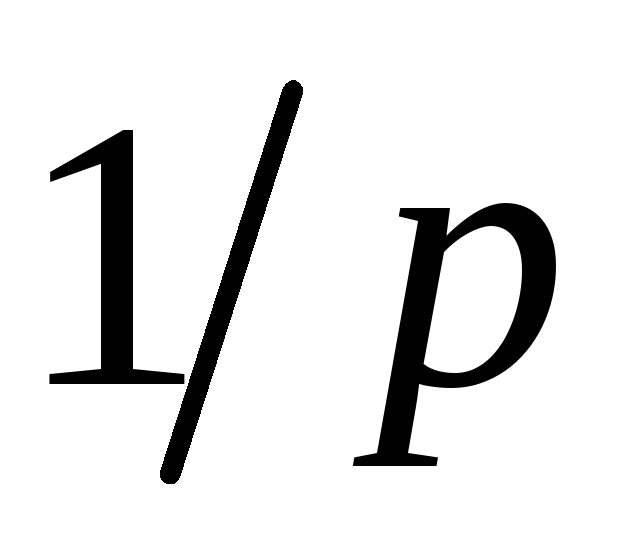
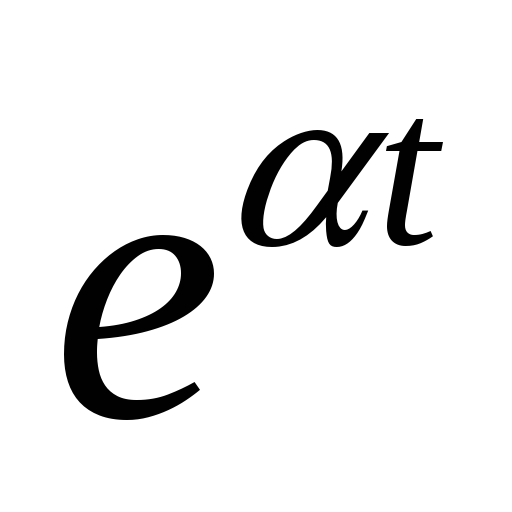
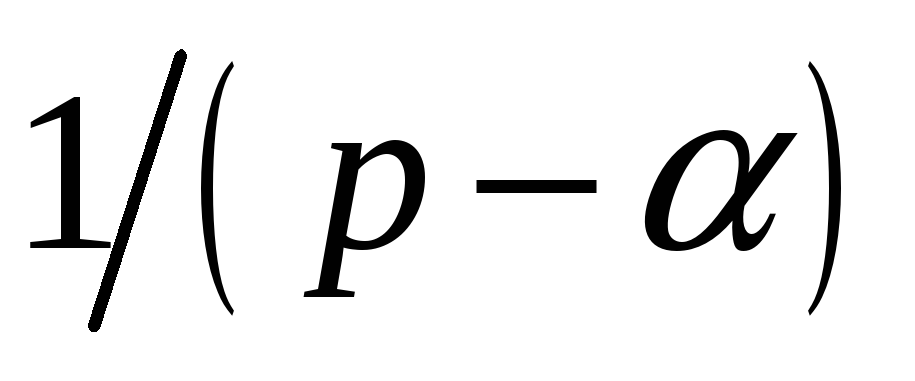
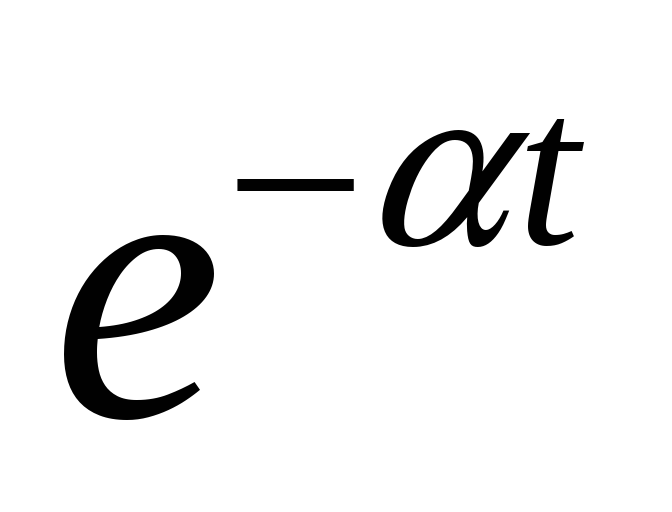
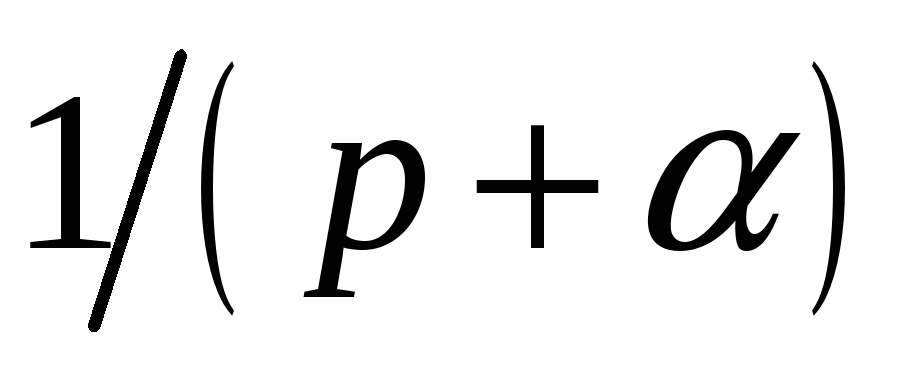
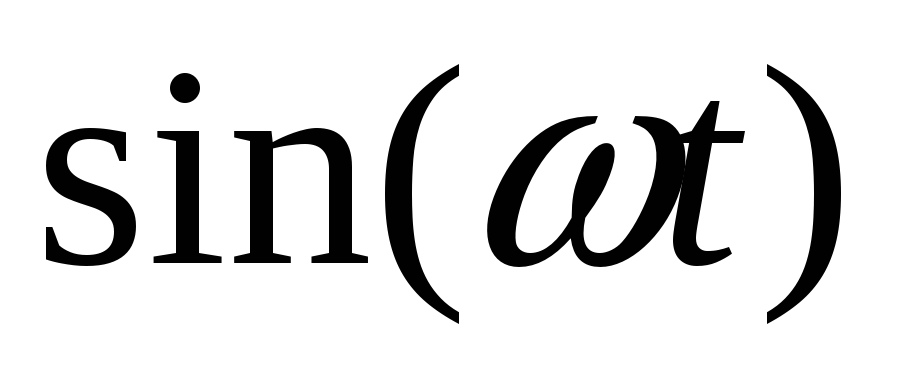
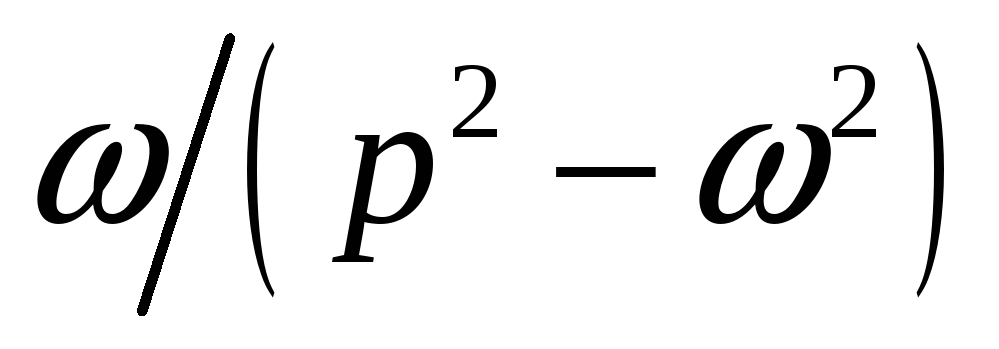
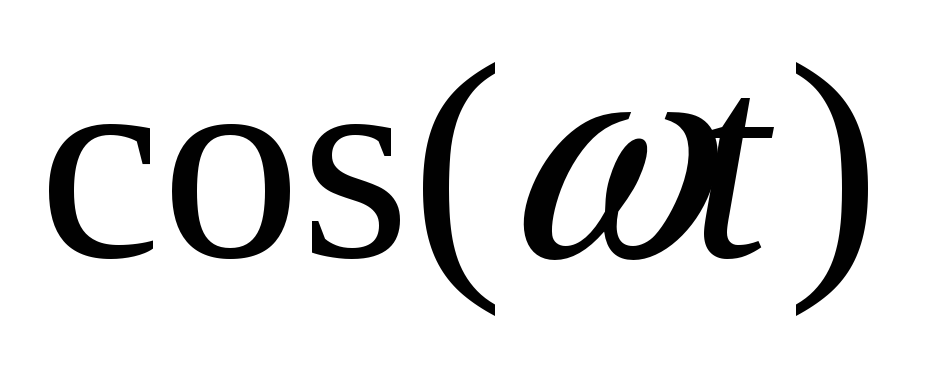
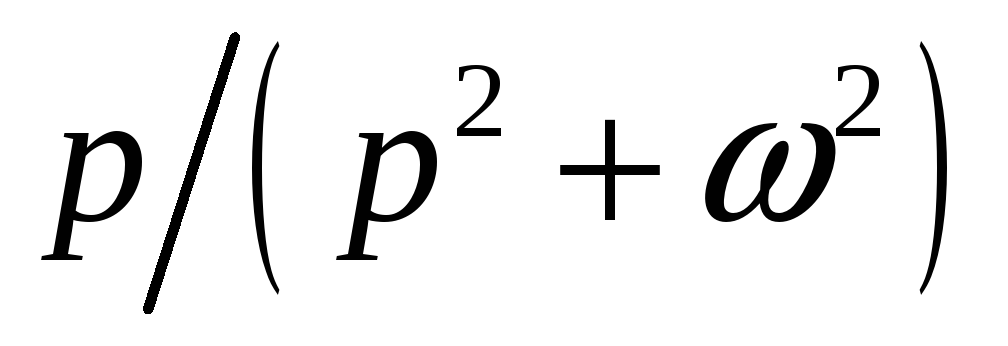
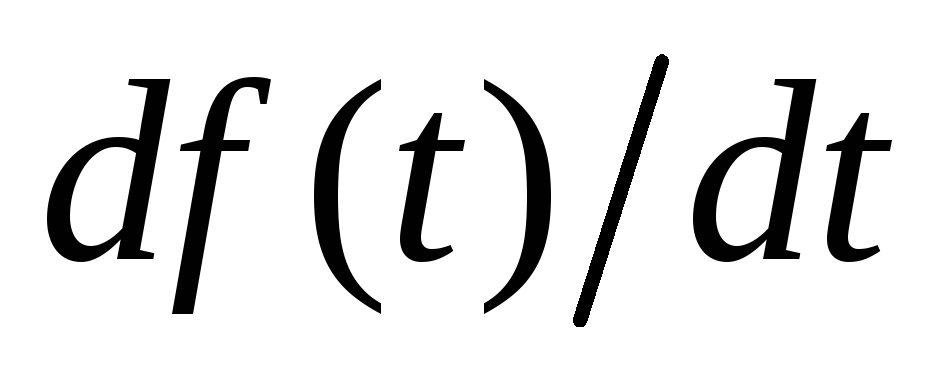
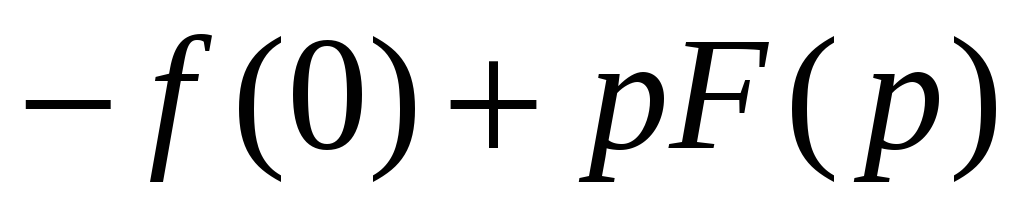
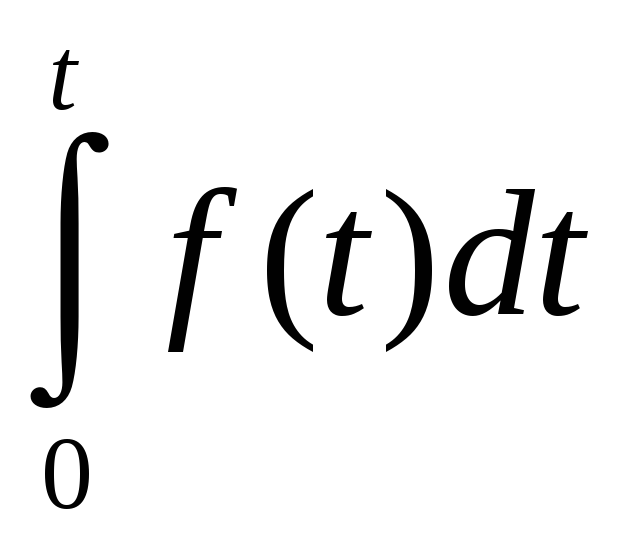
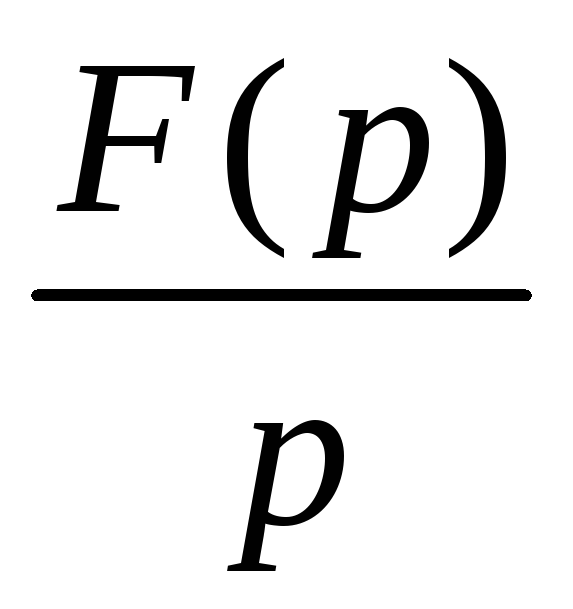
Вернёмся теперь к переходным процессам.

Итак, мы будем сопоставлять каждой функции его изображение. Например . С учётом полученной таблицы можно сопоставить каждому элементу его изображение:

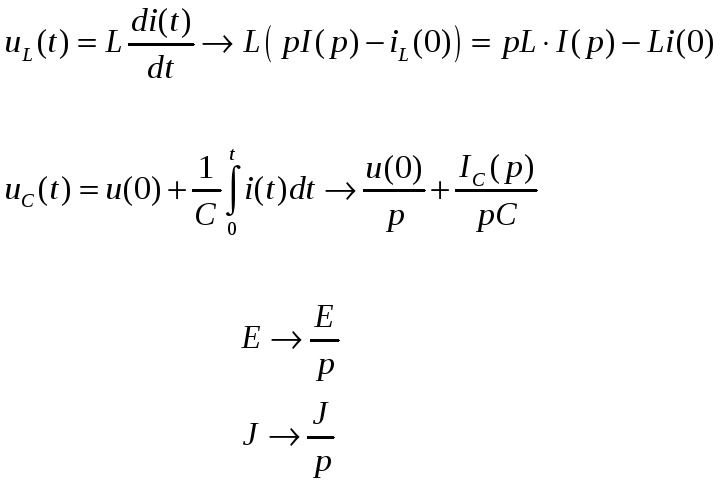
Заметим, что для того, что бы построить изображение схемы, нужны независимые начальные условия . После того как построена схема изображений, в пространстве изображений находятся желаемые токи и напряжения с использованием известных методов расчета (МКирхгофа, МУП, МКТ и т.д.). Для перехода от изображения к оригиналу (к временной зависимости) необходимо использовать теорему разложения:

где p_k – корни уравнения

где p_k – корни уравнения

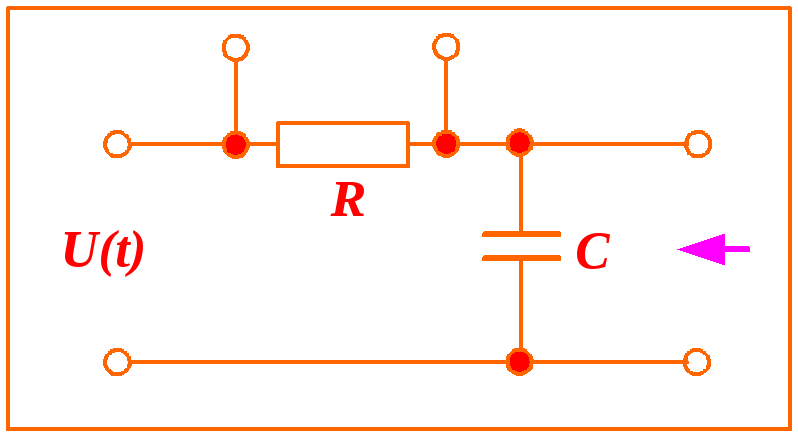
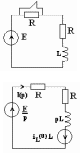
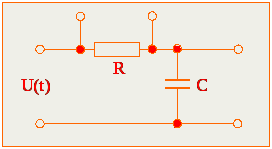
Пример: Определить ток источника напряжения если .

Рис

1. Ищем независимые начальные условия

2. Рисуем операторную схему замещения после коммутации и находим изображение тока

,

где:

.Находим корень знаменателя и его производную ,

Для определения оригинала используем теорему разложения

Переходные процессы в электрических цепях при воздействии импульсного напряжения. (Метод пространства состояний) Интегрирующие и дифференцирующие цепи (дифференцирование и интегрирование как операции фильтрации сигналов) Интеграл Дюамеля - аналитический метод расчета переходных процессов при импульсном воздействии Коэффициент заполнения .

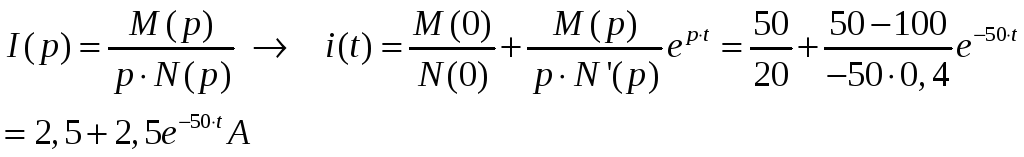
Лекция № 11