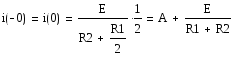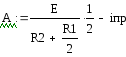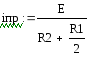- •Линейные электрические цепи
- •Постоянный ток
- •§ 1.1. Законы Кирхгофа
- •§ 1.2. Примеры использования законов Кирхгофа (методы расчетов)
- •§ 1.3. Матрично-топологический метод
- •§ 1.4. Метод контурных токов
- •§ 1.5 Баланс мощностей
- •§ 1.6. Метод контурных токов на основе матрично–топологического подхода
- •§ 1.7. Метод узловых потенциалов
- •§ 1.8. Метод узловых потенциалов на основе матрично-топологического метода
- •§ 1.9. Метод эквивалентных преобразований
- •§ 1.10. Преобразование треугольника в звезду и звезды в треугольник
- •§ 1.11. Метод эквивалентного генератора
- •§ 1.12 Характеристики эквивалентного генератора
- •§ 1.13. Метод наложения (метод суперпозиции).
- •Варианты расчетно–графических работ по расчету цепей постоянного тока
- •Пример выполнения расчетно-графичекой работы
- •Переменный ток
- •§2.1. Немного о комплексных числах
- •§2.3. Векторные диаграммы – фазовые соотношения между величинами
- •§2.4. Показания приборов
- •§2.5. Мощность в цепи переменного тока
- •§2.6. Цепи с индуктивно связанными элементами Последовательное соединение катушек с индуктивной связью.
- •§2.7. Построение диаграммы при встречном и согласном включениях индуктивностей с магнитной связью
- •§2.8. Расчет цепи с магнитно-связанными индуктивностями
- •§2.9. Построение векторной диаграммы
- •Мощность в цепи переменного тока с взаимной индуктивностью
- •§2.10. Трансформатор
- •§2.11. Резонанс напряжений
- •Ргр №2 Расчет линейной цепи синусоидального тока
- •Трехфазные цепи
- •§3.1 Метод симметричных составляющих
- •Переходные процессы §4.1 Переходные процессы в простейших цепях. Нулевые начальные условия
- •§4.2 Классический метод расчета переходного процесса. Первый и второй законы коммутации. Понятия о зависимых и независимых начальных условиях
- •§4.3 Метод расчета переходных процессов в цепи переменный тока
- •§4.4 Переходные процессы в цепи второго порядка
- •§4.5 Операторный метод расчёта переходных процессов
- •§4.6 Интеграл Дюамеля
- •Дельта функция Дирака и -ступенчатая функция Хевисайда
- •1.3. Импульсная переходная функции (весовая функция-функция Грина)
- •§4.6 Метод пространство состояний
- •Ргр №3 расчет переходных процессов в линейных цепях Цепь I-го порядка
- •Цепь II-го порядка
- •Схемы цепей I-го порядка
- •Схемы цепей II-го порядка
- •Операционные усилители
- •§2.3 Общее рассмотрение каскада на операционном усилителе с отрицательной обратной связью
- •Контрольная работа-№1
- •Линии с распределенными параметрами
- •§5.1 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в начале линии
- •§5.2 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии
- •§5.3 Линии без потерь
- •§5.4 Коэффициент отражения
- •§5.5 Действующие значения напряжения и тока вдоль линии без потерь
- •§5.6 Стоячие волны
- •§5.7 Входное сопротивление линии без потерь при холостом ходе
- •§5.8 Аналогия между уравнениями линии с распределенными параметрами и уравнениями четырехполюсника
- •Нелинейные резистивные цепи постоянного тока
- •§6.1 Линеаризация нелинейной характеристики
- •§6.2 Расчет магнитных цепей
§4.2 Классический метод расчета переходного процесса. Первый и второй законы коммутации. Понятия о зависимых и независимых начальных условиях
До сих пор мы рассматривали относительно простые задачи переходного процесса с независимыми начальными условиями – это задачи на определения тока переходного процесса через индуктивность и напряжения переходного процесса на ёмкости. Задачи определения тока переходного процесса через сопротивление или через источник напряжения решаются сложнее. Для понимания сложных переходных процессов очень важно понимать, что такое зависимые и независимые начальные условия. Начнем рассмотрения этих понятий с первого и второго законов коммутации.
В электрической цепи, не может быть мгновенного изменения накопленной в электрических и магнитных полях энергии
![]() .
.
Так как энергия электрического поля конденсатора и энергия магнитного поля индуктивной катушки равны соответственно
![]() ,
,
то это означает, что в момент коммутации остаются неизменными напряжения на обкладках конденсатора и токи в индуктивных катушках. Для перераспределения энергии требуется время – это процесс инерционный, не мгновенный. Поэтому существуют два закона коммутации.
Первый закон (правило) коммутации –
ток через индуктивность непосредственно
до коммутации
![]() равен
току через индуктивность после коммутации
равен
току через индуктивность после коммутации
![]() :
:
![]() . (*)
. (*)
Второй закон (правило) коммутации –
напряжение на ёмкости непосредственно
до коммутации
![]() равно
напряжению на ёмкости после коммутации
равно
напряжению на ёмкости после коммутации
![]() :
:
![]() . (*)
. (*)
Это есть независимые начальные условия. Независимыми они называются потому, что независимо от того до или после коммутации мы их наблюдаем, они всё равно одинаковы и равны, и поэтому знаки – и + в выражениях (**) опускают. Важно помнить, что независимые начальные условия определяются в схеме до коммутации. Таким образом, существует только два независимых начальных условия – это напряжение на конденсаторе и ток через индуктивность.
Иначе дело обстоит с зависимыми начальными условиями, например с током через ёмкость или с током через источник напряжения:
![]() .
.
или с напряжением на индуктивности или на источнике тока:
![]() .
.
Зависимые начальные условия могут
изменятся скачком непосредственно до
и после коммутации. То есть их значения
«зависят» от того наблюдаем мы их до
или после коммутации. Зависимые
начальные условия определяются в схеме
после коммутации. (При этом в
послекоммутационной схеме ёмкость
заменяется на источник напряжения
равный величине
![]() и
направленный против ёмкостного тока
а индуктивность заменяется на источник
тока равный
и
направленный против ёмкостного тока
а индуктивность заменяется на источник
тока равный
![]() и направлен он по индуктивному току ).
и направлен он по индуктивному току ).
Запишем последовательность действий для определения зависимых начальных условий:
-
Определяем независимые начальные условия в схеме до коммутации – ток через индуктивность
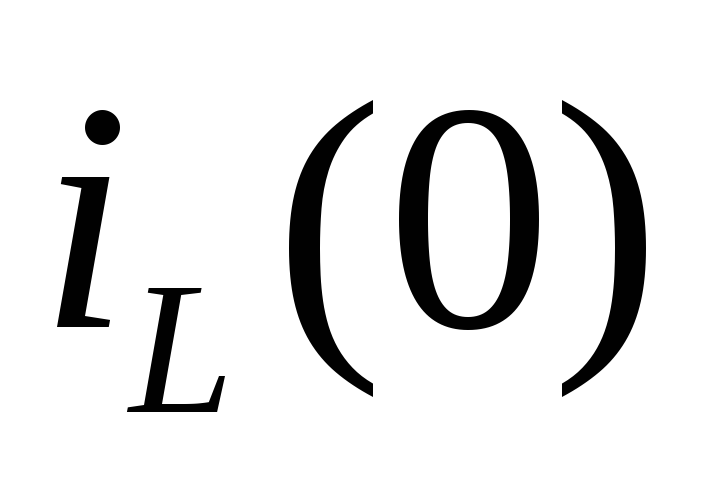 и напряжения на конденсаторе
и напряжения на конденсаторе
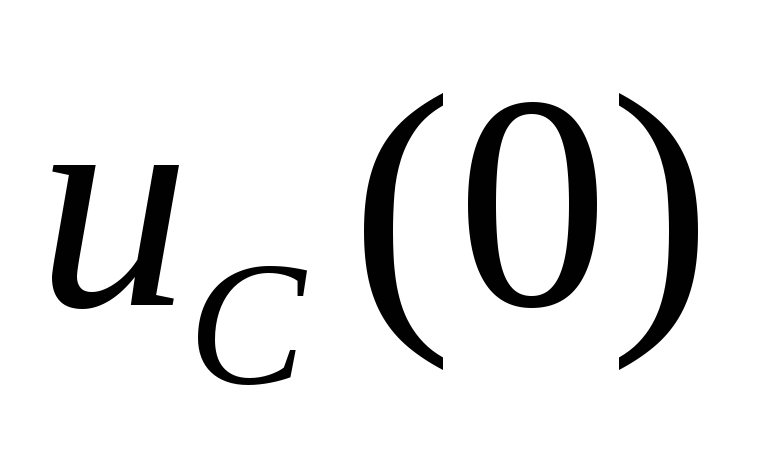
-
Заменяем в схеме после коммутации индуктивность–
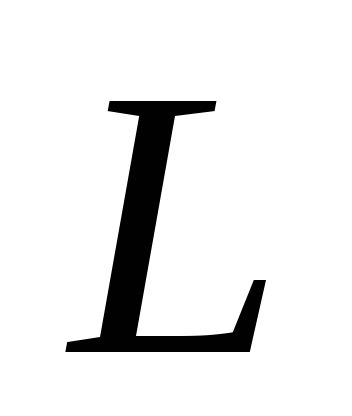 ,
источником тока равным значению
,
источником тока равным значению
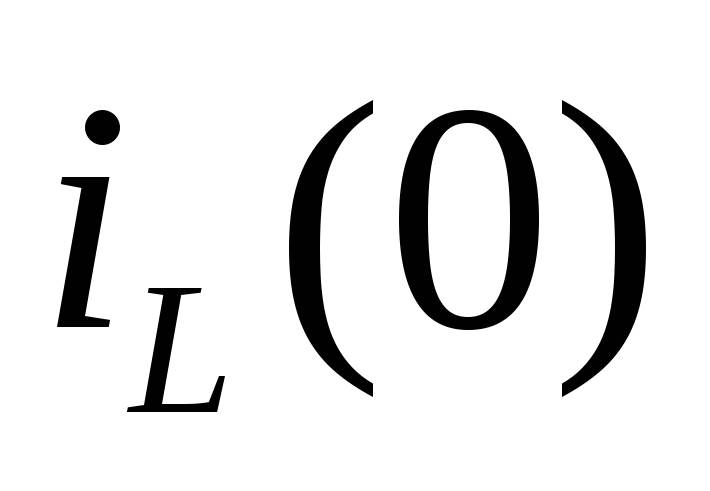 ,
а емкость –
,
а емкость – источником напряжения равным значению
источником напряжения равным значению
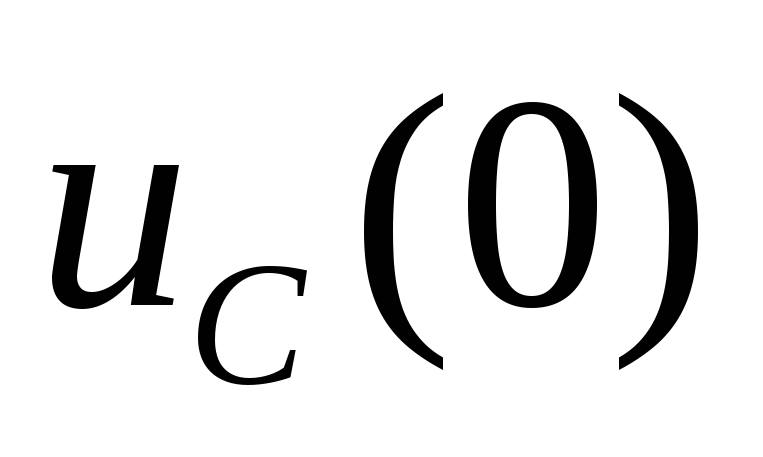 .
.
-
Далее находим интересующие нас зависимые начальные условия.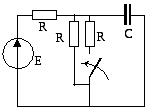
Теперь можно приступить к решению примеров с зависимыми и независимыми начальными условиями.
Пример: Определить независимые
![]() и зависимые начальные условия
и зависимые начальные условия
![]() для заданной схемы, если заданы величины:
для заданной схемы, если заданы величины:
![]() .
.
|
|
Определяем зависимые начальные условия
в схеме после коммутации заменяем при
этом ёмкость на источник напряжения:.
![]()
![]()
|
|
Определяем независимые начальные
условия в схеме до коммутации:
![]() .
.
Определяем зависимые начальные условия
в схеме после коммутации заменяем при
этом заменяем индуктивность на источник
тока равный
![]() .
.
|
|
![]()
Примеры
|
ПЕРЕХОДНЫЕ ПРОЦЕССЫ Независимые начальные условия
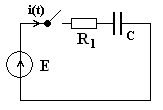
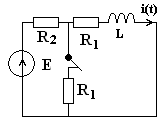
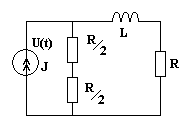
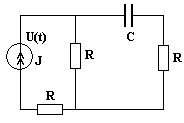
Пример-1. рис-1 Дано :
Ищем решения в виде:
1) iпр определяет принуждённую составляющую в схеме после коммутации :
2) из ННУ определяет константу интегрирования A в схеме до коммутации :
3) Корень характеристического уравнения через входное сопротивление в схеме после коммутации :
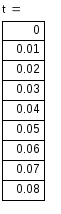
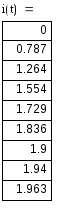
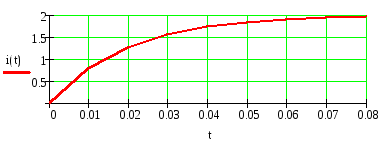
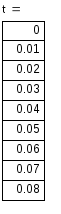
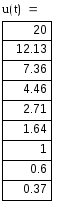
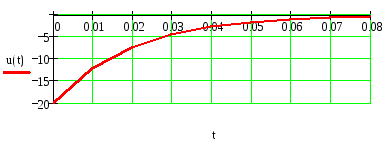
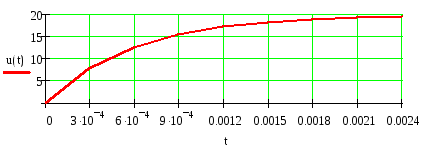
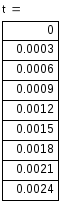
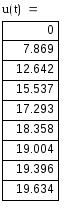
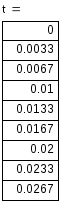
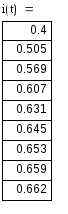
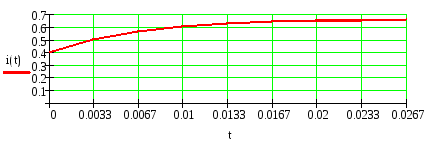
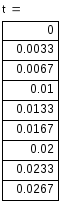
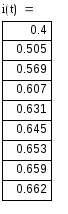
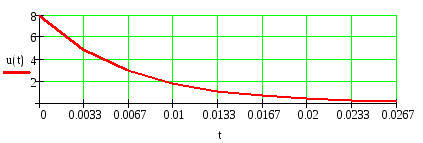
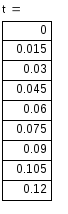
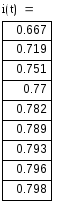
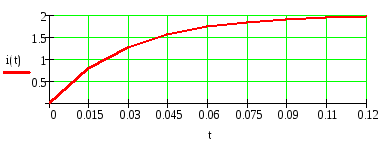
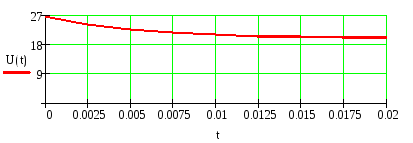
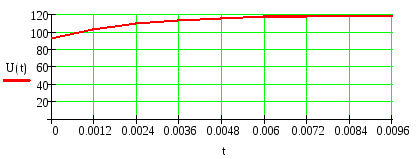
4) Записываем окончательное решение и строим график i(t) :
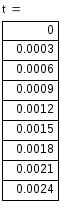
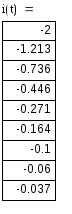
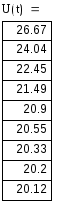
4) Определяем напряжение на индуктивности U(t) :
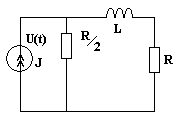
Пример-2. рис-2
Ищем решения в виде:
1) iпр определяет принуждённую составляющую схеме после коммутации : Рис-2
2) из ННУ определяет константу интегрирования A в схеме до коммутации :
3) Корень характеристического уравнения через входное сопротивление в схеме после коммутации :
4) Записываем окончательное решение и строим график i(t) :
4) Определяем напряжение на индуктивности U(t) :
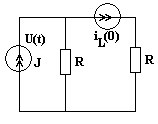
Пример-3. рис-3 Ищем решения в виде:
1) iпр определяет принуждённую составляющую схеме после коммутации :
2) из ННУ определяет константу интегрирования A в схеме до коммутации :
3) Корень характеристического уравнения через входное сопротивление в схеме после коммутации :
4) Записываем окончательное решение и строим график i(t) :
4) Определяем напряжение на индуктивности U(t) :
Зависимые и независимые начальные условия
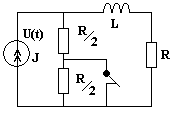
Пример- 4. Рис- 4 Дано :
Рис- 4 Ищем решения в виде:
1) iпр определяет принуждённую составляющую схеме после коммутации : Рис-
5
2) определяет ННУ в схеме до коммутации :
3) определяет ЗНУ в схеме после коммутации ( рис - 5 ) :
4) Корень характеристического уравнения через входное сопротивление в схеме после коммутации :
5) Записываем окончательное решение и строим график i(t) :
Зависимые и независимые начальные условия Пример-5. Рис- 6 Дано :
Рис- 6 Ищем решения в виде:
1) Uпр определяет принуждённую составляющую схеме после коммутации ( рис - 7 ):
2) определяет ННУ в схеме до коммутации ( рис - 8 ):
Рис- 7
Рис- 8 Рис- 9 3) определяет ЗНУ в схеме после коммутации ( рис - 9 ) :
4) Корень характеристического уравнения через входное сопротивление в схеме после коммутации (рис - 7) :
5) Записываем окончательное решение и строим график i(t) :
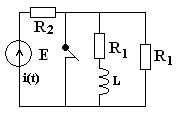
Зависимые и независимые начальные условия Пример- 6. Рис- 10 Дано :
Ищем решения в виде: Рис- 10
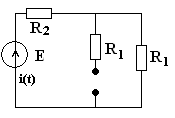
1) Uпр определяет принуждённую составляющую схеме после коммутации ( рис - 11 ):
2) определяет ННУ в схеме до коммутации ( рис - 12 ):
Рис- 11
Рис- 13 Рис- 14 Рис- 12 3) определяет ЗНУ в схеме после коммутации ( рис - 13 и 14 ) :
4) Корень характеристического уравнения через входное сопротивление в схеме после коммутации (рис - 7) :
5) Записываем окончательное решение и строим график i(t) :
|
Лекция № 10

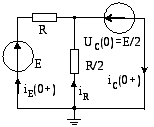
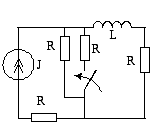
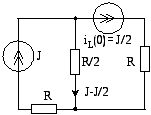
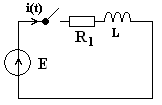 Рис.1:
Рис.1: