- •Линейные электрические цепи
- •Постоянный ток
- •§ 1.1. Законы Кирхгофа
- •§ 1.2. Примеры использования законов Кирхгофа (методы расчетов)
- •§ 1.3. Матрично-топологический метод
- •§ 1.4. Метод контурных токов
- •§ 1.5 Баланс мощностей
- •§ 1.6. Метод контурных токов на основе матрично–топологического подхода
- •§ 1.7. Метод узловых потенциалов
- •§ 1.8. Метод узловых потенциалов на основе матрично-топологического метода
- •§ 1.9. Метод эквивалентных преобразований
- •§ 1.10. Преобразование треугольника в звезду и звезды в треугольник
- •§ 1.11. Метод эквивалентного генератора
- •§ 1.12 Характеристики эквивалентного генератора
- •§ 1.13. Метод наложения (метод суперпозиции).
- •Варианты расчетно–графических работ по расчету цепей постоянного тока
- •Пример выполнения расчетно-графичекой работы
- •Переменный ток
- •§2.1. Немного о комплексных числах
- •§2.3. Векторные диаграммы – фазовые соотношения между величинами
- •§2.4. Показания приборов
- •§2.5. Мощность в цепи переменного тока
- •§2.6. Цепи с индуктивно связанными элементами Последовательное соединение катушек с индуктивной связью.
- •§2.7. Построение диаграммы при встречном и согласном включениях индуктивностей с магнитной связью
- •§2.8. Расчет цепи с магнитно-связанными индуктивностями
- •§2.9. Построение векторной диаграммы
- •Мощность в цепи переменного тока с взаимной индуктивностью
- •§2.10. Трансформатор
- •§2.11. Резонанс напряжений
- •Ргр №2 Расчет линейной цепи синусоидального тока
- •Трехфазные цепи
- •§3.1 Метод симметричных составляющих
- •Переходные процессы §4.1 Переходные процессы в простейших цепях. Нулевые начальные условия
- •§4.2 Классический метод расчета переходного процесса. Первый и второй законы коммутации. Понятия о зависимых и независимых начальных условиях
- •§4.3 Метод расчета переходных процессов в цепи переменный тока
- •§4.4 Переходные процессы в цепи второго порядка
- •§4.5 Операторный метод расчёта переходных процессов
- •§4.6 Интеграл Дюамеля
- •Дельта функция Дирака и -ступенчатая функция Хевисайда
- •1.3. Импульсная переходная функции (весовая функция-функция Грина)
- •§4.6 Метод пространство состояний
- •Ргр №3 расчет переходных процессов в линейных цепях Цепь I-го порядка
- •Цепь II-го порядка
- •Схемы цепей I-го порядка
- •Схемы цепей II-го порядка
- •Операционные усилители
- •§2.3 Общее рассмотрение каскада на операционном усилителе с отрицательной обратной связью
- •Контрольная работа-№1
- •Линии с распределенными параметрами
- •§5.1 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в начале линии
- •§5.2 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии
- •§5.3 Линии без потерь
- •§5.4 Коэффициент отражения
- •§5.5 Действующие значения напряжения и тока вдоль линии без потерь
- •§5.6 Стоячие волны
- •§5.7 Входное сопротивление линии без потерь при холостом ходе
- •§5.8 Аналогия между уравнениями линии с распределенными параметрами и уравнениями четырехполюсника
- •Нелинейные резистивные цепи постоянного тока
- •§6.1 Линеаризация нелинейной характеристики
- •§6.2 Расчет магнитных цепей
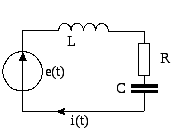
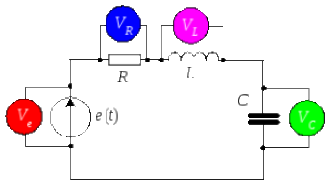
§2.11. Резонанс напряжений
|
|
|
|
|
Зависимость емкостного сопротивления
![]() от частоты имеет гиперболическую
зависимость. При увеличении частоты
уменьшается емкостное сопротивление
и при этом ток в цепи с емкостью
увеличивается. То есть чем быстрее
изменяется ток тем меньше емкостное
сопротивление. При уменьшении частоты
до нуля емкостное сопротивление
становится бесконечным. То есть емкость
не пропускает постоянный ток. И, наоборот,
при увеличении частоты емкостное
сопротивление уменьшается, и ток в цепи
увеличивается. Вспомним, что емкость
пропускает ток смещения.
от частоты имеет гиперболическую
зависимость. При увеличении частоты
уменьшается емкостное сопротивление
и при этом ток в цепи с емкостью
увеличивается. То есть чем быстрее
изменяется ток тем меньше емкостное
сопротивление. При уменьшении частоты
до нуля емкостное сопротивление
становится бесконечным. То есть емкость
не пропускает постоянный ток. И, наоборот,
при увеличении частоты емкостное
сопротивление уменьшается, и ток в цепи
увеличивается. Вспомним, что емкость
пропускает ток смещения.
В цепи с последовательно соединенными
элементами
![]() сопротивление записывается в виде:
сопротивление записывается в виде:
![]()
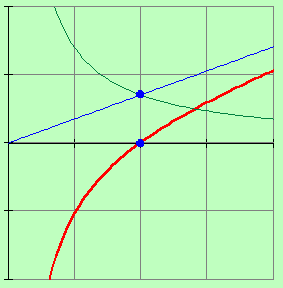
Будем изменять частоту входного напряжения в цепи. При изменении частоты будут изменяться сопротивления реактивных элементов. При увеличении частоты уменьшается емкостное сопротивление и увеличивается индуктивное сопротивление, и наоборот. При постепенном изменении частоты может наступить такой момент, когда емкостное и индуктивное сопротивления сравняются, и будет выполняться равенство
![]() .
.
Полученная частота называется частотой свободных колебаний. При такой частоте возникаю свободные колебания в цепи. Колебания электрической цепи не связанные с источником энергии, называются собственными или свободными.
В нашем случае при рассмотрении
последовательной цепи эти колебания
возбуждены внешним источником
![]() .
При резонансной частоте общее сопротивление
цепи уменьшается, так как индуктивное
сопротивление компенсируется емкостным
сопротивлением
.
При резонансной частоте общее сопротивление
цепи уменьшается, так как индуктивное
сопротивление компенсируется емкостным
сопротивлением
![]() .
.
При этом ток в цепи возрастает, Ток и напряжение совпадают по фазе. При дальнейшем увеличении частоты индуктивное сопротивление становится больше емкостного, и реактивное сопротивление становится индуктивным.
|
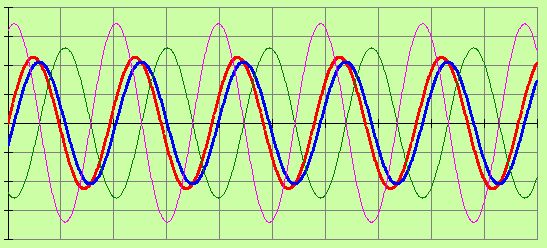
Волновая диаграмма напряжений. Цвета напряжений соответствуют цветам вольтметров |
|
|
Схема соответствия цветов векторов напряжений и вольтметров |
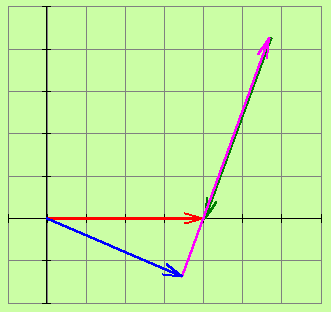
Векторная диаграмма напряжений |
![]()
Режим электрической цепи при последовательном соединении участков с индуктивностью и ёмкостью, характеризующийся равенством индуктивного и ёмкостного сопротивлений, называют резонансом напряжений.
Напряжения на индуктивности и ёмкости при резонансе могут значительно превышать напряжение на входе, которое равно напряжению на активном сопротивлении.
Отметим, что частоты, при которых наблюдаются фазовый и амплитудный резонансы, не совпадают с частотой собственных колебаний контура (они совпадают только в теоретическом случае, когда катушка индуктивности и конденсатор без потерь).
Добротность
![]() определяется соотношением:
определяется соотношением:
![]()
Чем выше добротность контура Q (и уже полоса пропускания) тем выше селективность контура (лучше избирательная способность) При резонансе происходит совпадение по фазе входного напряжения e(t) и тока i(t) протекающего в контуре. Характер сопротивления становится чисто активным вследствие совпадения по величине емкостного и индуктивного сопротивлений.
|
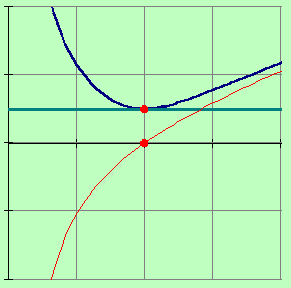
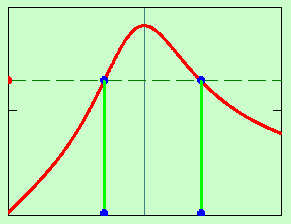
АЧХ- |
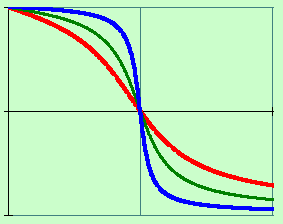
ФЧХ- |
Ширина АЧХ
![]() зависит
от добротности. Ширина АЧХ определяется
на высоте 0,707 от амплитудного значения
(См. рис). Определим граничные частоты
зависит
от добротности. Ширина АЧХ определяется
на высоте 0,707 от амплитудного значения
(См. рис). Определим граничные частоты
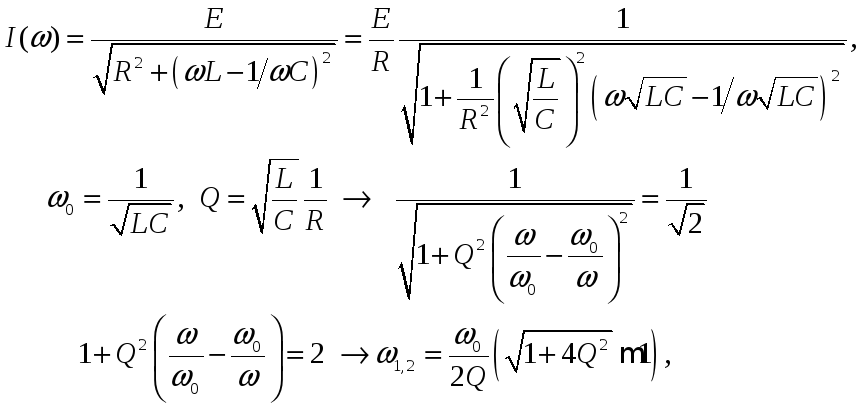
и полосу пропускания
![]()
Таким образом,
рассмотренная схема является полосовым
фильтром, рассмотренный фильтр эффективно
пропускает частоты, находящиеся в полосе
![]() увеличивая их относительный вклад.
Относительный вклад всех остальных
частоты уменьшается
увеличивая их относительный вклад.
Относительный вклад всех остальных
частоты уменьшается
|
|
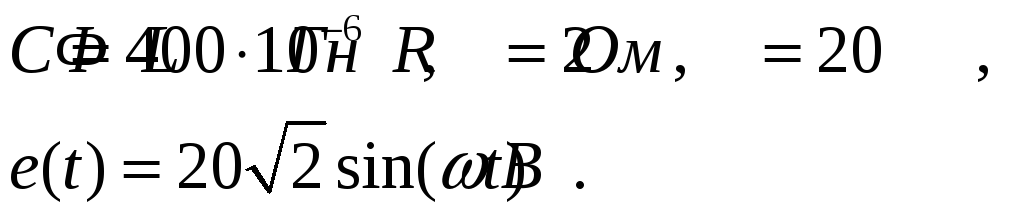 Определить
добротность контура, ток, полосу
пропускания и граничные частоты.
Определить
добротность контура, ток, полосу
пропускания и граничные частоты.
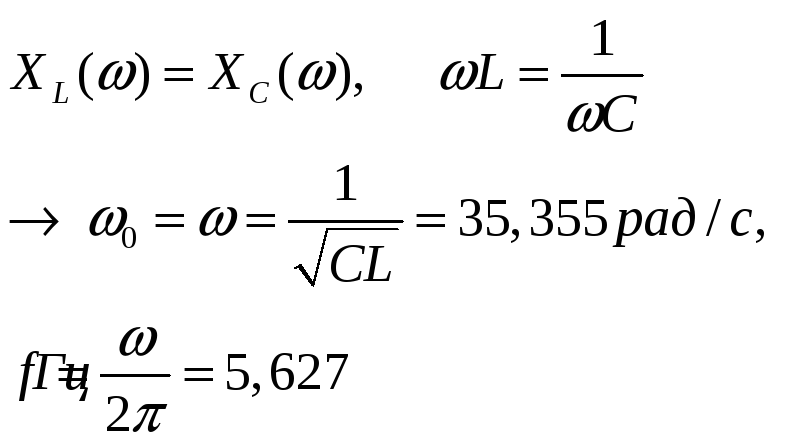 .
.
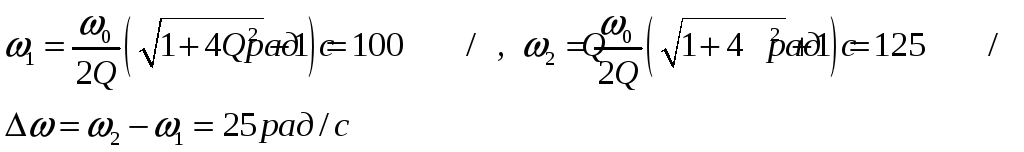
Полоса пропускания
устанавливается на высоте сигнала
равного значению
![]() ,
,
![]() –максимальное
значение тока.
–максимальное
значение тока.