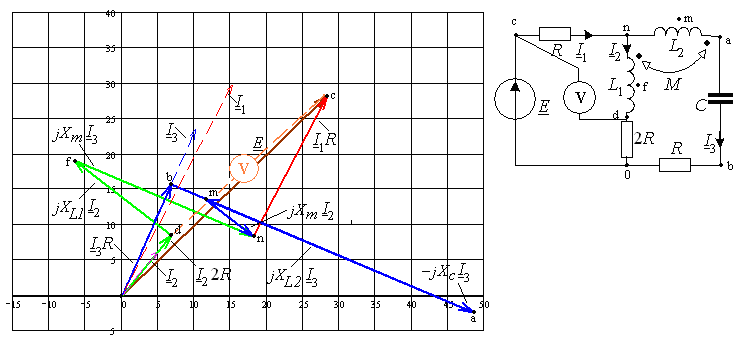
§2.9. Построение векторной диаграммы

Для построения векторной диаграммы в первую очередь нужно задаться масштабом тока и напряжения. Следующим этапом строится лучевая диаграмма токов, а затем по отношению к ней строится топографическая диаграмма напряжений. Учитывая, что ток и напряжение на активном сопротивлении находятся в фазе, векторы напряжения и тока на диаграмме следует откладывать параллельно друг другу, и направленными в одну сторону. Напряжение на индуктивности опережает ток индуктивности на 90 градусов, следовательно, вектор напряжения откладывается перпендикулярно вектору тока с опережением (откладывается против часовой стрелки). Напряжение на емкости отстает от тока емкости на 90 градусов, следовательно, вектор напряжения откладывается перпендикулярно вектору тока с отставанием (откладывается по часовой стрелке).

Приведем пример построения диаграммы для нашей схемы. Откладываем в масштабе токи и напряжения (см. диаграмму). Вычислим необходимые значения напряжений на элементах.

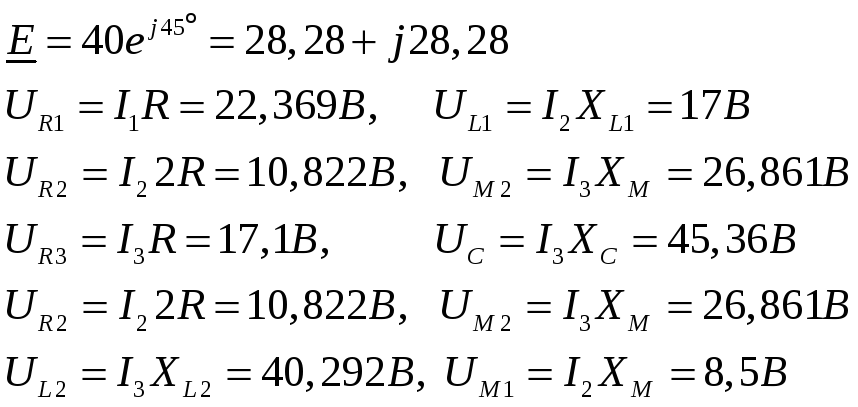
Определим показания вольтметра:

или

Мощность в цепи переменного тока с взаимной индуктивностью

Полная мощность, как и прежде, определяется выражением

, P - активная мощность, Q - реактивная мощность.

Активная и реактивная мощности определяются соотношениями соответственно:

.

Здесь токи ветвей, в которых находится индуктивности. Знак плюс выбирается, когда в цепи согласное включение катушек. В противном случае выбирается знак минус.

Ниже приводится электрическая схема, собранная в программно-интегрированной среде ElectronicsWorkbench с развязкой индуктивной связи. При развязке индуктивной связи получается отрицательная индуктивность. В место отрицательной индуктивности можно поставить эквивалентную емкость, которая определяется выражением

.

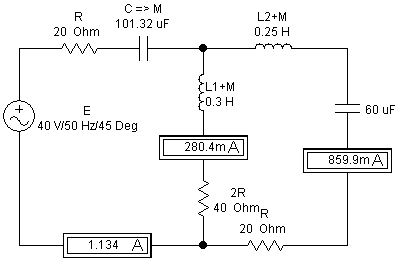
Приведем схему рассмотренной задачи собранную в среде ElectronicsWorkbench.

Ниже приводится программа вычисления в программно-интегрированной среде MathCAD.

Магнитносвязанные катушки

Лекция № 7

§2.10. Трансформатор

Электрическая цепь состоит из контуров различного назначения. Может оказаться, что для различных контуров цепи требуется отличающиеся по величине напряжения. Для преобразования переменного напряжения и для перераспределения энергии между контурами цепи, широко применяется такое устройство как трансформатор.

Функциональные и конструктивные особенности трансформаторов весьма разнообразны. Мы рассмотрим линейный трансформатор, в котором отсутствуют нелинейные эффекты. Воздушные трансформаторы являются линейными.

Трансформатор состоит из двух или нескольких индуктивно связанных катушек. Рассмотрим простой двухобмоточный трансформатор.

Двухобмоточный трансформатор состоит из двух обмоток – первичной и вторичной. К первичной обмотке подводится питание а ко вторичной подсоединяется нагрузка–потребитель энергии. Токи и напряжения, относящиеся к первичной и вторичной обмоткам называются первичными и вторичными соответственно.

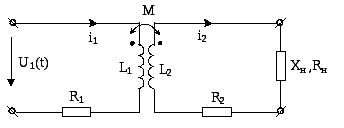
Рис. Трансформатор

Для усиления магнитной связи используют ферромагнитные сердечники вокруг которых наматываются обмотки трансформатора (но при этом трансформатор становится нелинейным).

Запишем второй закон Кирхгофа для трансформатора, введя обозначения элементов первичной и вторичной обмоток:

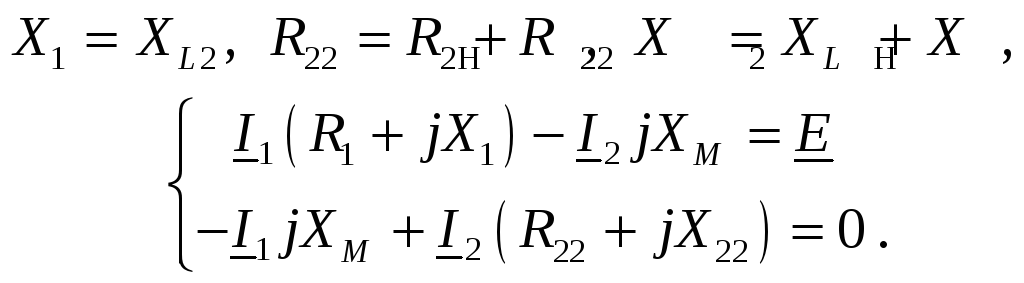(50)

Умножим первое уравнение на , а второе уравнение на и затем сложим. В результате получим выражение тока первичной обмотки через входное напряжение и сопротивления, вносимые вторичной обмоткой :

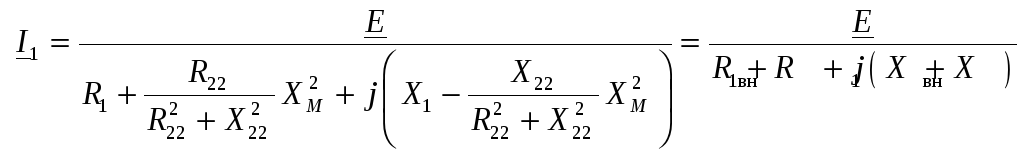, (51)

где .

Это выражение называется приведение сопротивлений вторичной обмотки к сопротивлениям первичной обмотки. Из этого выражения вытекает следующее. Для того, что бы трансформатор передавал максимальную мощность во вторичную обмотку необходимо, чтобы выполнялось соотношение:

(52)

Построим качественно векторные диаграммы для трансформатора при различных нагрузках:

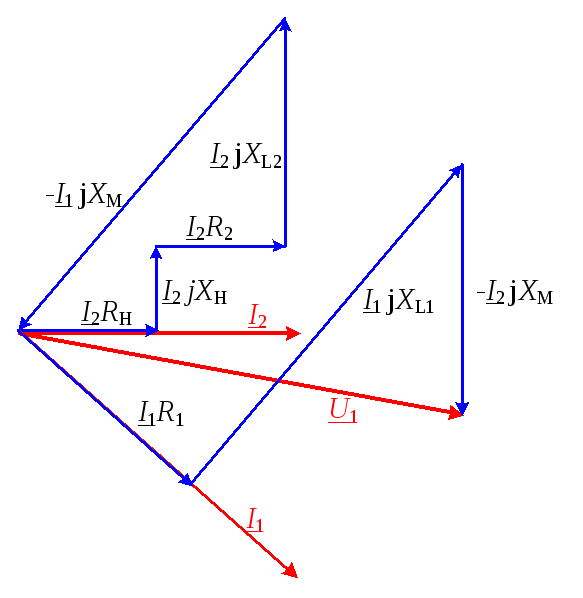
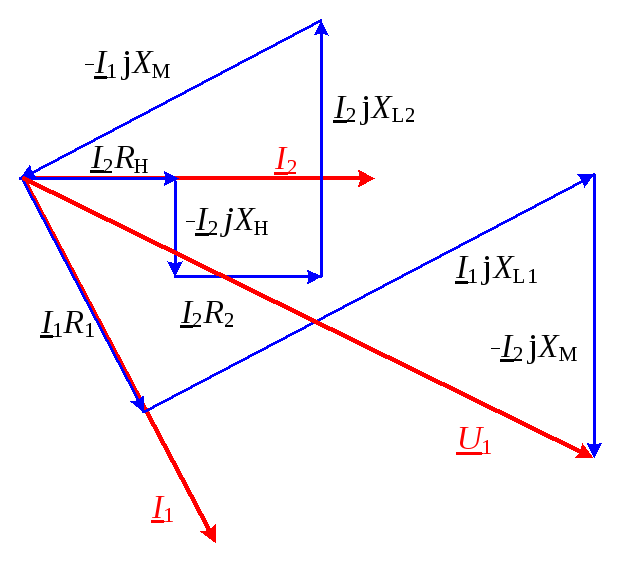
а б Рис. Векторная диаграмма напряжений трансформатора при нагрузках : а) 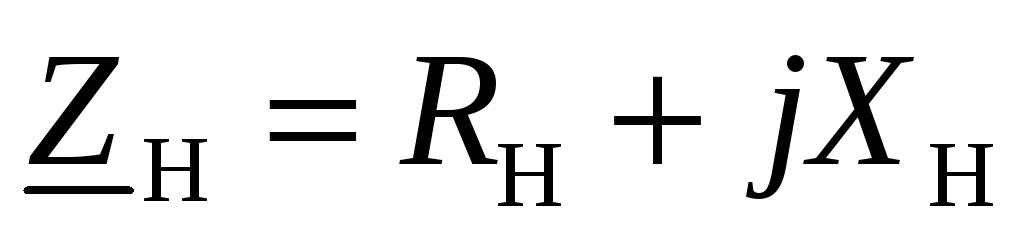и б)

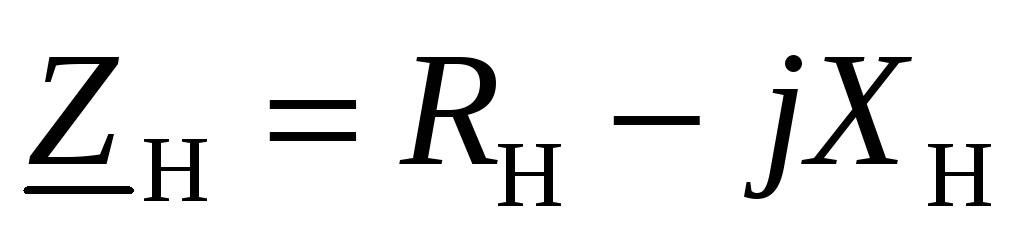
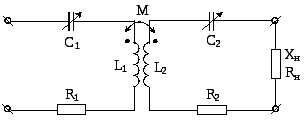
Что бы добиться выполнения соотношение (52) в первичную и во вторичную цепи трансформатора включаются переменные емкости, что позволяет варьировать реактивные составляющие сопротивлений первичной и вторичной цепях, рис.

Рис.

Для схемы приведенной на рисунке реактивные составляющие будут определятся выражениями:

.

Если разрешить первое выражение (52) относительно , то можно получить:

.

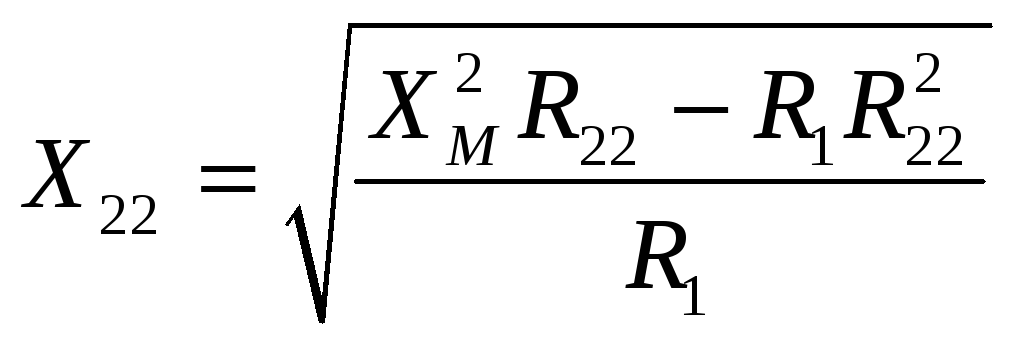Последнее выражение показывает, что при выполнении неравенства:

Невозможно получить максимальную мощность во внесенном сопротивлении .