- •Линейные электрические цепи
- •Постоянный ток
- •§ 1.1. Законы Кирхгофа
- •§ 1.2. Примеры использования законов Кирхгофа (методы расчетов)
- •§ 1.3. Матрично-топологический метод
- •§ 1.4. Метод контурных токов
- •§ 1.5 Баланс мощностей
- •§ 1.6. Метод контурных токов на основе матрично–топологического подхода
- •§ 1.7. Метод узловых потенциалов
- •§ 1.8. Метод узловых потенциалов на основе матрично-топологического метода
- •§ 1.9. Метод эквивалентных преобразований
- •§ 1.10. Преобразование треугольника в звезду и звезды в треугольник
- •§ 1.11. Метод эквивалентного генератора
- •§ 1.12 Характеристики эквивалентного генератора
- •§ 1.13. Метод наложения (метод суперпозиции).
- •Варианты расчетно–графических работ по расчету цепей постоянного тока
- •Пример выполнения расчетно-графичекой работы
- •Переменный ток
- •§2.1. Немного о комплексных числах
- •§2.3. Векторные диаграммы – фазовые соотношения между величинами
- •§2.4. Показания приборов
- •§2.5. Мощность в цепи переменного тока
- •§2.6. Цепи с индуктивно связанными элементами Последовательное соединение катушек с индуктивной связью.
- •§2.7. Построение диаграммы при встречном и согласном включениях индуктивностей с магнитной связью
- •§2.8. Расчет цепи с магнитно-связанными индуктивностями
- •§2.9. Построение векторной диаграммы
- •Мощность в цепи переменного тока с взаимной индуктивностью
- •§2.10. Трансформатор
- •§2.11. Резонанс напряжений
- •Ргр №2 Расчет линейной цепи синусоидального тока
- •Трехфазные цепи
- •§3.1 Метод симметричных составляющих
- •Переходные процессы §4.1 Переходные процессы в простейших цепях. Нулевые начальные условия
- •§4.2 Классический метод расчета переходного процесса. Первый и второй законы коммутации. Понятия о зависимых и независимых начальных условиях
- •§4.3 Метод расчета переходных процессов в цепи переменный тока
- •§4.4 Переходные процессы в цепи второго порядка
- •§4.5 Операторный метод расчёта переходных процессов
- •§4.6 Интеграл Дюамеля
- •Дельта функция Дирака и -ступенчатая функция Хевисайда
- •1.3. Импульсная переходная функции (весовая функция-функция Грина)
- •§4.6 Метод пространство состояний
- •Ргр №3 расчет переходных процессов в линейных цепях Цепь I-го порядка
- •Цепь II-го порядка
- •Схемы цепей I-го порядка
- •Схемы цепей II-го порядка
- •Операционные усилители
- •§2.3 Общее рассмотрение каскада на операционном усилителе с отрицательной обратной связью
- •Контрольная работа-№1
- •Линии с распределенными параметрами
- •§5.1 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в начале линии
- •§5.2 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии
- •§5.3 Линии без потерь
- •§5.4 Коэффициент отражения
- •§5.5 Действующие значения напряжения и тока вдоль линии без потерь
- •§5.6 Стоячие волны
- •§5.7 Входное сопротивление линии без потерь при холостом ходе
- •§5.8 Аналогия между уравнениями линии с распределенными параметрами и уравнениями четырехполюсника
- •Нелинейные резистивные цепи постоянного тока
- •§6.1 Линеаризация нелинейной характеристики
- •§6.2 Расчет магнитных цепей
![]()
Рекомендуемая Литература
-
Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. Основы теории цепей М.: Энергоатомиздат, 1989, 528с
-
Л.А. Бессонов. Теоретические основы электротехники: Электрические цепи. М.: Гардарики, 1984, 638с.
-
К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. Теоретические основы электротехники. Т1,Т2,Т3. М.: Высшая школа, 2003.
-
А.С.Касаткин, М.В.Немцов. Электротехника. М.: Академия, 2003, 544с.
Лектор – Профессор, д.ф.-м.н. Исаев Юсуп Ниязбекович.
E-mail: Isaev_yusup@mail.ru (18 лекций-36 часов)
|
CОДЕРЖАНИЕ
Г-I. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ……………………………………………... Постоянный ток ……………………………....………………………………………………… § 1.1. Законы Кирхгофа…………………………………………….......................................... § 1.2. Примеры использования законов Кирхгофа (методы расчетов) ........................... § 1.3. Матрично-топологический метод…………………………....…….............................. § 1.4. Метод контурных токов…………………………....……............................................... § 1.5. Баланс мощностей………………………………………………………………………. § 1.6. Метод контурных токов на основе матрично–топологического подхода……….. § 1.7. Метод узловых потенциалов………………....…........................................................... § 1.8. Метод узловых потенциалов на основе матрично-топологического метода…… § 1.9. Метод эквивалентных преобразований………………………..…………………….. § 1.10. Преобразование треугольника в звезду и звезды в треугольник………………… § 1.11. Метод эквивалентного генератора………………………………………………….... § 1.12. Характеристики эквивалентного генератора…………………...………………….. § 1.13. Метод наложения (метод суперпозиции)…………….…..…………………………... Варианты расчетно-графических работ по расчету цепей переменного тока РГР №1 – Расчет линейной цепи постоянного тока…...……………………………………….... Пример выполнения расчетно-графичекой работы…………………………………….…. §2 Переменный ток ...……....……....…..........…………………………………………………. §2.1.Немногоо комплексных числах………………………………………………………...... §2.2. Синусоидальные токи и напряжения. Метод комплексных амплитуд (Символический метод)………………………………………………………………………... §2.3. Векторные диаграммы – фазовые соотношения между величинами……………… §2.4. Показания приборов………….…………………………................................................... §2.5. Мощность в цепи переменного тока.…………………………………………………... §2.6. Цепи с индуктивно связанными элементами Последовательное соединение катушек с индуктивной связью.…………………………………………………………….… §2.8. Построение диаграммы при параллельном соединении индуктивностей с магнитной связью…………………………………………………………………………..… §2.9. Расчет цепи с магнитно-связанными индуктивностями……………………………. §2.10. Построение векторной диаграммы……………………………………………………………………………………….. §2.11. Трансформатор...…....……....……....…....……....……....…..........………………….. §2.12. Резонанс напряжений ……………………………………………………………..… РГР №2 Расчет линейной цепи синусоидального тока §3 Трехфазные цепи…………....…....…....……....…....……....……....…..............…………
|
3 3 3 5 6 9 10 10 12 14 16 18 20 21 18 16 17 18 22 28 30 31
34 35 35
36
37
39 41 45 |
Линейные электрические цепи
Лекция № 1
Постоянный ток
Напомнить об обозначенияx, падении напряжения,
![]() ,
,
и о величинах сопротивлений источников
питания
![]()
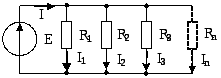
§ 1.1. Законы Кирхгофа
|
Рис. 1 |
![]() (1)
(1)
Результирующий ток I , протекающий в ветви с ЭДС, будет равен сумме токов всех ветвей без ЭДС, то есть
![]() (2)
(2)
Если подставить выражение (1) в (2), то можно получить:
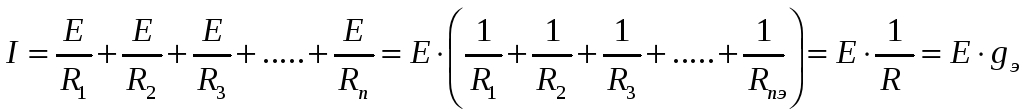 (3)
(3)
Коэффициент пропорциональности между током и ЭДС называется проводимостью и измеряется в сименсах (См). Итак, мы получили важную формулу, позволяющую определить результирующее – эквивалентное сопротивление схемы с параллельным соединением проводников:
![]() (4)
(4)
|
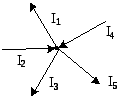
Рис. 2 |
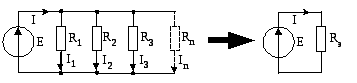
В частном случае, когда в цепи два сопротивления, выражение (4) можно переписать:
![]() (5)
(5)
Это выражение следует запомнить, потому что в электротехнике часто приходится преобразовывать цепь с двумя параллельно включенными сопротивлениями.
Отметим полезную информацию, которая содержится в выражении (4). Если вы правильно подсчитали результирующее (эквивалентное) сопротивление схемы параллельно соединённых проводников, то величина результирующего сопротивления должна быть меньше величины самого маленького сопротивления цепи. Теперь вернёмся к выражению (2). Это выражение называется первым законом Кирхгофа, и формулируется следующим образом: Алгебраическая сумма токов в узле равняется нулю.
|
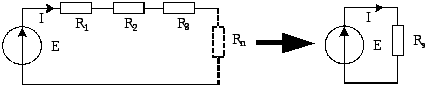
Рис. 3 |
![]() . (6)
. (6)
|
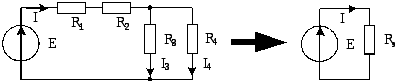
Рис. 4 |
![]() (7)
(7)
По закону Ома, ЭДС в результирующей цепи равняется произведению силы тока на результирующее сопротивление. Проделав несложные преобразования можно получить:
![]() (8)
(8)
где
![]() и
т.д. В результате мы получили второй
закон Кирхгофа,
который формулируется следующим
образом: алгебраическая
сумма напряжений для любого замкнутого
контура равняется алгебраической сумме
ЭДС контура:
и
т.д. В результате мы получили второй
закон Кирхгофа,
который формулируется следующим
образом: алгебраическая
сумма напряжений для любого замкнутого
контура равняется алгебраической сумме
ЭДС контура:
![]() (9)
(9)
|
Рис. 5 |
![]() (10)
(10)
Рассмотрим правило
параллельных ветвей для ветвей
с токами
![]() (Рис
5.). Напряжения на ветвях одинаково,
следовательно,
(Рис
5.). Напряжения на ветвях одинаково,
следовательно,
![]() и
и ![]() (11)
(11)
Решая систему уравнений относительно
![]() ,
получаем правило параллельных ветвей:
,
получаем правило параллельных ветвей:
![]() .
(12)
.
(12)
Это правило иногда называют ”правилом
разброса”, так как
общий ток ветвей 3 и 4 разбрасывается по
ветвям с коэффициентами пропорциональности
![]() .
.