Задание с4 Уметь решать различные задачи с параметрами.
1. Для каждого значения параметра решите уравнение:
1) (а²-1)х
- (2а²+а-3) = 0, где а - параметр.
;
2. Найдите значения параметра р, при которых уравнение (1-р)х² + 2рх – р – 2 = 0 имеет два различных положитель-
ных корня.
3. Найдите значения параметра р, при которых уравнение рх² + 2(р-1)х + р – 3 = 0 имеет два различных отрицатель-
ных корня.
4. Найдите значения параметра р, при которых уравнение (1-р)х² + 2(р-3)х + 4 – р = 0 имеет корни разных знаков.
5. При каких значениях параметра а оба корня уравнения ах² + 4 ах + 1 – 2а + 4а² = 0 меньше чем -1?
6. При каких значениях параметра а один корень уравнения ах² + х + 1 = 0 больше 2, а другой корень меньше чем 2?
7. При каких значениях параметра а оба корня уравнения х² - ах + 2 = 0 лежат на промежутке (0; 3)?
8. Найдите значение параметра а, при которых 1 лежит между корнями уравнения 2ах² - 2х – 3а – 2 = 0.
9. Найдите значение параметра а, при которых уравнение (а-1)х² - 2ах + 2 – 3а = 0 имеет единственное решение,
удовлетворяющее неравенству х >1.
10. При каких значениях параметра р все корни уравнения (2-р)х² - 3рх + 2р = 0 больше чем 0,5?
11. При каких значениях параметра а корни уравнения х² - 2ах + а² - а = 0 расположены на отрезке [-2;6]?
12. Найдите значения параметра а, при которых один корень уравнения (а-2)х² - 2(а+3)х + 4а = 0 меньше чем 2,
а другой корень больше чем 3.
13. При каких значениях параметра а уравнения х² + ах + 1 = 0 и х² + х + а = 0 имеют общий корень?
14. При каких значениях параметра а уравнения (1-а)х² + 2х – 4а = 0 и ах² - 4х + 4а = 0 равносильны?
15.
Найдите все значения параметра р, при
которых уравнение
имеет
четыре различных
действительных корня.
16.
Найдите все значения параметра а, при
каждом из которых уравнение
имеет
единственное
решение.
17.
При каких значениях параметра а уравнение
имеет
два различных решения?
18.
При каких значениях параметра р уравнение
имеет два различных корня?
19. При каких значениях параметра с уравнение имеет единственное решение?
20.
Найдите значения параметра а, при которых
уравнение
имеет
два различных корня.
21.
Найдите значения параметра с, при котором
уравнение
имеет
единственный корень.
22. Найдите все значения параметра р, при которых уравнение 4Sin3x – 3Cos6x = p не имеет корней.
23. При каких значениях параметра с уравнение 2Cos2x – Cos4x = c имеет хотя бы один корень?
24.
При каких значениях параметра а уравнение
не имеет корней?
25.
Найдите все значения параметра а, при
которых уравнение
имеет один корень.
26.
При каких значениях параметра а уравнение
имеет
два действительных корня?
Задание с4 Задачи с параметрами.
27.
При каких значениях параметра а система
уравнений
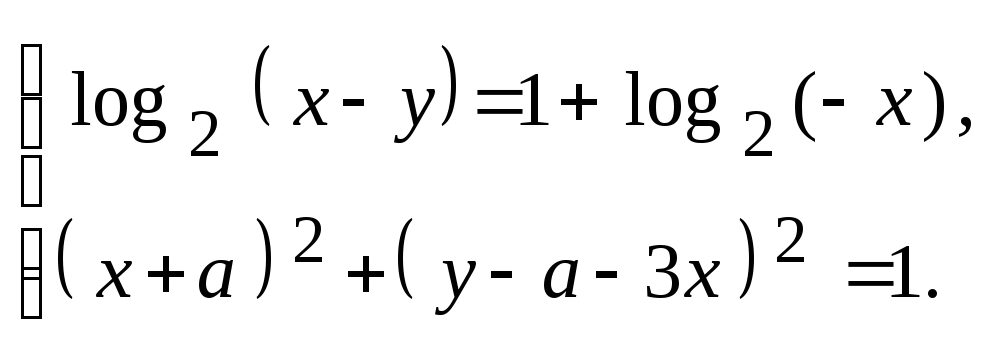имеет
единственное решение?
28.
Найдите все значения параметра а, при
которых уравнение
имеет единственное решение.
29.
Найдите все значения параметра р, при
которых уравнение
имеет
одно решение.
30.
При каких значениях параметра а уравнение
имеет
решения?
31.
При каких а уравнение
имеет решение?
32.
При каких значениях а найдутся такие
значения х , что числа
в указанном порядке обра-
зуют арифметрическую прогрессию?
33.
Найдите все значения параметра р, при
которых найдутся такие значения х, что
числа
в указанном порядке образуют некоторую арифметическую прогрессию.
34.
Найдите все значения параметра а, при
которых уравнение
имеет единственное решение.
35.
Найдите значения параметра р, при которых
уравнение
имеет единственное решение.
36. Для каждого значения параметра а решите неравенство:
37. При каких значениях параметра а данное неравенство выполняется при любых действительных значениях х?
1) (а + 4 ) х² - 2aх + 2а – 6 < 0 ; 2 ) ( a² - 1 ) x² + 2 ( a – 1 ) x + 2 > 0.
38. Найдите все значения параметра р, при которых значение многочлена f(x) = (p² - 1)x² + 2(p – 1)x + 1 положительно
при любых действительных х.
39.
При каком наименьшем целом значении р
функция f(x)
= -x³
+
x²
- 5x
+ 2 убывает на все числовой прямой?
40.
При каком наименьшем целом р функция
возрастает на всей числовой прямой?
41. При каком значении а, для всех х таких, что хε (1;2) выполняется неравенство х² + ах + а² + 6а < 0?
42. Найдите все значения параметра а, для которых неравенство х² - ах + а > 0 верно при всех х, удовлетворяющих
неравенству
.
43. При каких значениях параметра а каждое решение неравенства х² - 3х + 2 < 0 будет содержаться среди решений
неравенства ах² - ( 3а + 1)х + 3 ≥ 0.
44. Найдите значения параметра а, при которых область определения данной функции f(x) совпадаете со множеством
всех действительных чисел:
45.
Найдите все значения параметра а, при
которых область определения функции
содержит
пять целых чисел.
46.
Найдите все значения параметра а, при
которых область определения функции
содержит
отрезок длиной 4, состоящий из отрицательных чисел.
47.
Найдите значения параметра а, при которых
область определения функции
содержит
отрезок длины 3, состоящий из положительных чисел.