Домашнее задание:

14. Постройте графики следующих уравнений:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) ;

и) .

14. Запишите уравнение прямой, проходящей через точку A(-1;1) параллельно прямой, заданной следующим уравнением:

а) ; б) ; в) ; г) .

14. (Лицей-8, 1998 г.) График функции проходит через точки A(1;4) и B(3;8). Найдите a и b и постройте график этой функции.

15. (Лицей-8, 1999 г.) График линейной функции проходит через точки M(-1;2) и N(3;-4). Задайте формулой эту функцию и постройте ее график. Определите, при каких значениях x значение y: а) равно нулю; б) больше нуля; в) меньше нуля.

16. (Лицей-8, 2002 г.) Сумма ординаты и абсциссы точки B равна 5. Найдите координаты точки B, если известно, что она лежит на прямой . На координатной плоскости изобразите прямую и точку B. При каких значениях аргумента x функция y больше нуля?

17. (Лицей-8, 2001 г.) При каких значениях b три прямые пересекаются в одной точке: ; ; ?

18. (Лицей-8, 2003 г.) Найдите значение b, при котором графики функций и пересекаются в точке с ординатой -4. Постройте эти графики и найдите координаты точки их пересечения. Постройте точку, симметричную точке пересечения графиков относительно оси ординат и запишите ее координаты.

19. (Лицей-8, 1995 г.) При каком d прямые и пересекаются в точке, принадлежащей прямой ?

20. (Лицей-8, 1997 г.) Прямые и пересекаются в точке M(x₀;y₀). Положение этой точки на прямой зависит от значения a. 1) Найдите абсциссу x₀ точки M(x₀;y₀) при a=1. 2) Какое число следует подставить вместо a, чтобы точка пересечения имела абсциссу x₀=‑1?

7. Решение и исследование линейных уравнений.

Линейным называется уравнение вида , где k и b – некоторые числа. Решение линейного уравнения сводится к выражению x через k и b. В случае, когда k≠0, уравнение имеет единственный корень . Если же k=0, возможны две ситуации:

• k=0 и b=0: В этом случае уравнение приобретает вид , и любое число является его корнем (т.е. уравнение в этом случае имеет бесчисленное множество решений);

• k=0, b≠0: В этом случае уравнение приобретает вид , и ни при каком x оно не обращается в верное равенство (т.е. уравнение в этом случае не имеет корней).

Задачи:

1. Решите следующие уравнения:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

2. (Лицей-8, 2000 г.) При каких значениях a уравнение имеет корень: ?

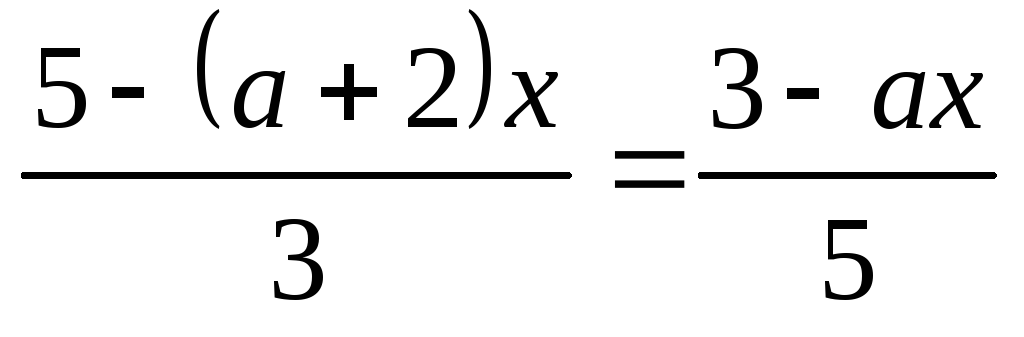3. (Лицей-8, 2002 г.) При каком значении числа a уравнение не имеет решений: ?

4. (Лицей-8, 2005 г.) При каком значении параметра k корнем уравнения является любое число?

5. Найдите значения a, при которых уравнение имеет не менее двух корней.

6. Определите значения a, при которых число 1 является корнем уравнения .

7. (Лицей-8, 2004 г.) При каких значениях параметра a корень уравнения на 3 больше, чем корень уравнения ?

8. (Лицей-8, 2001 г.) Решите уравнение и определите, при каких значениях параметра c оно имеет корень: .